Three thin, uniform, indentical rods each or mass M and length L are joined as shown. Find the M.I. about an axis passing through O and perpendicular to the plane.
We know, for rod, M.I. of rod about an axis passing through an end and ⊥ar to length is ML2/3. Apply this formula directly.

I0=I1+I2+I3=ML23×3=ML2
Topper's Solved these Questions
Similar Questions
Two identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.
 View Solution
View SolutionTwo thin uniform rods A (M.L) and B (3M,3L) are joined as shown. Find the M.I. about an axis passing through the center of mass of system of rods and perpendicular to the length.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Four thin rods of same mass m and same length L form a square as shown in the figure. M.I. of this system about an axis through center O and perpendicular to its plane is
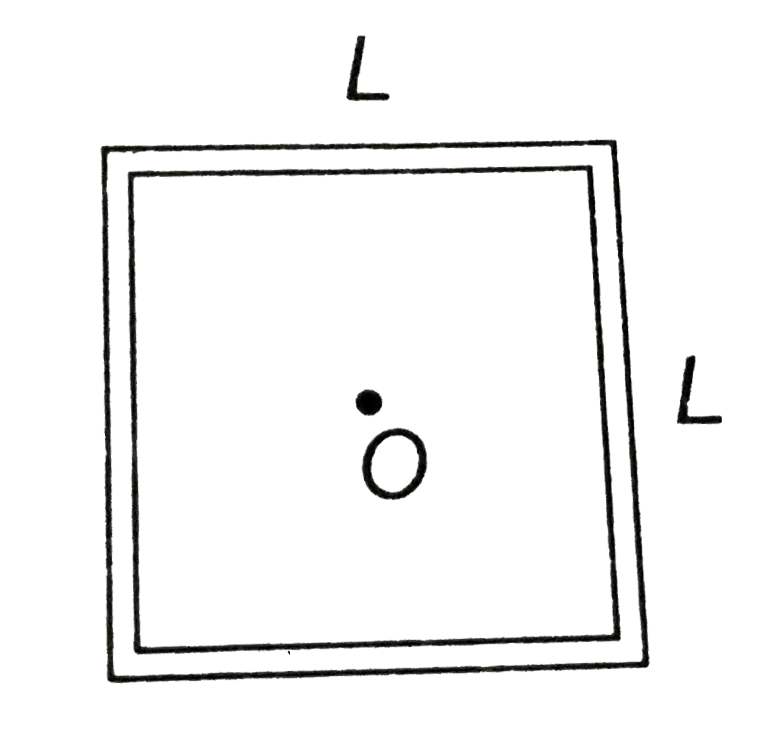 A4mL23BmL23CmL26D4mL23
A4mL23BmL23CmL26D4mL23 - Question 2 - Select One
Calculate the M.I. of a thin uniform ring about an axis tangent to the ring and in a plane of the ring, if its M.I. about an axis passing through the centre and perpendicular to plane is 4kgm2.
A12kgm2B3kgm2C6kgm2D9kgm2
Three particles A,B and C of masses m,2m and 3m are placed on a straight line of length 2L as shown. Find the M.I. about an axis passing through B and perpendicular to the line AC.
View SolutionThree thin unifrom circular discs each of mass M and radius R are placed touching each other on a horizontal surface such that an equilateral triangle is formed, when the center of three discs are joined. Find the M.I. about an axis passing through the center of mass system of discs and perpendicular to the plane.
View SolutionA rod of mass M, length L is bent in the form of hexagon. Then MOI about axis passing through geometric centre and perpendicular to plane of body will be
View SolutionThree identical roads each of mass M and L are joined to form an equilateral triangle. Find the M.I. about an axis perpendicular to the plane of triangle and passing through
(a) center of triangle
(b) mid-point of a rod and
(c ) one vertex of triangle.View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is
 View Solution
View SolutionTwo particles of masses m and 2m are placed at separation L. Find the M.I. about an axis passing through the center of mass and perpendicular to the line joining the point masses.
View Solution

