The angular position of a swinging door is described by θ=5+10t+20t2. Determine the angular position, angular speed and angular acceleration at t=2s.
θ=5+10t+20t2
ω=dθdt=10+40t
α=dωdt=40
At t=2s,
θ=5+10(2)+20(2)2=5+20+80=105rad
ω=10+40(2)=90rad/s
α=40rad/s2
Topper's Solved these Questions
Similar Questions
Introduction || Angular Position and Angular Displacement
View SolutionThe angular position of a point on the rim of a rotating wheel is given by θ=4t3−2t2+5t+3 rad. Find
(a) the angular velocity at t=1s,
(b) the angular acceleration at t=2s.
(c ) the average angular velocity in time interval t=0 to t=2s and
(d) the average angular acceleration in time interval t=1 to t=3s.View Solution
Knowledge Check
- Question 1 - Select One
The angular position of a line of a disc of radius r = 6cm is given by θ=10−5t+4t2 rad , the average angular velocity between 1 and 3s is
Aπrad s−1B11rad s−1C22rad s−1D5.5rad s−1 - Question 2 - Select One
The angular displacement of a particle is given by θ=t3+2t+1, where t is time in seconds. Its angular acceleration at t=2s is
A14rads−2B17rads−2C12rads−2D9rads−2
A point on a body performing pure rotation is 10cm from the axis of rotation of body. Angular position of the point from reference line is given by θ=0.5e2t, where θ is in Radian and t in second. The acceleration of the point at t=0 is
View SolutionThe angular position of a point on a rotating wheel is given by θ=2.0+4.0t2+2.0t3, where θ is in radians and t is in seconds. At t = 0, what are (a) the point's angular position and (b) its angular velocity? ( c) What is its angular velocity at t = 3.0 s? (d) Calculate its angular acceleration at t = 4.0 s. (e) Is its angular acceleration constant?
View SolutionThe angular displacement of particle (in radian) is given by θ=t2+t. Calculate angular velocity at t=2 second.
View SolutionWe are given the job of designing a large horizontal ring that will rotate around a vertical axis and that will have a radius of r = 33.1 m. Passengers will enter through a door in the outer wall of the ring and then stand next to that wall. We decide that for the time interval t = 0 to t = 2.30 s, the angular position θ(t) of a reference line on the ring will be given by
θ=ct3,
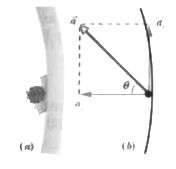
with c=6.39×10−2rad/s3. After t = 2.30 s, the angular speed will be held constant until the end of the ride. Once the ring begins to rotate, the floor of the ring will drop away from the riders but the riders will not fall - indeed, they feel as though they are pinned to the wall. For the time t = 2.20 s, let's determine a rider's angular speed ω, linear speed ν, angular acceleration α, tangential acceleration at, radial acceleration ar, and acceleration →a.View SolutionA solid body rotates with angular velocity →ω=3tˆi+2t2ˆjrad/s. Find
(a) the magnitude of angular velocity and angular acceleration at time t=1s and
(b) the angle between the vectors of the angular velocity and the angular acceleration at that moment.View SolutionA solid body rotates with angular velocity ω=ati+bt2j, where a=0.50rad/s2, b=0.060rad/s3, and i and j are the unit vectors of the x and y axes. Find:
(a) the moduli of the angular velocity and the angular acceleration at the moment t=10.0s,
(b) the angle between the vectors of the angular velocity and the angular acceleration at that moment.View Solution

