We are given the job of designing a large horizontal ring that will rotate around a vertical axis and that will have a radius of r = 33.1 m. Passengers will enter through a door in the outer wall of the ring and then stand next to that wall. We decide that for the time interval t = 0 to t = 2.30 s, the angular position θ(t) of a reference line on the ring will be given by
θ=ct3,
with c=6.39×10−2rad/s3. After t = 2.30 s, the angular speed will be held constant until the end of the ride. Once the ring begins to rotate, the floor of the ring will drop away from the riders but the riders will not fall - indeed, they feel as though they are pinned to the wall. For the time t = 2.20 s, let's determine a rider's angular speed ω, linear speed ν, angular acceleration α, tangential acceleration at, radial acceleration ar, and acceleration →a.
(1) The angular speed ω is given by Eq. (ω=dθ/dt). (2) The linear speed ν (along the circular path) is related to the angular speed (around the rotation axis) by Eq. (ν=ωr). (3) The angular acceleration α is given by Eq. (α=dω/dt). (4) The tangential acceleration at (along the circular path) is related to the angular acceleration (around the rotation axis) by Eq. (at=αr). (5) The radial acceleration ar is given Eq. (ar=ω2r). (6) The tangential and radial accelerations are the (perpendicular) components of the (full) acceleration →a.
Calculations: Let.s go through the steps. We first find the angular velocity by taking the time derivative of the given angular position function and then substituting the given time of t = 2.20 s:
ω=dθdt=ddt(ct3)=3ct2
= 3(6.39×10−2rad/s3)(2.20s)2
= 0.928 rad/s.
the linear speed just then is
ν=ωr=3ct2r
= 3(6.39×10−2rad/s3)(2.20s)2(33.1m)
= 30.7 m/s.
Next, let.s tackle the angular acceleration by taking the time derivative of Eq.
α=dωdt=ddt(3ct2)=6ct
= 6(6.39×10−2rad/s3)(2.20s)=0.843rad/s2.
The tangential acceleration then follows from Eq.
a1=αr=6ctr
= 6(6.30×10−2rad/s3)(2.20s)2(33.1m)
= 27.91m/s2≈27.9m/s2.
or 2.8 g Eq. tells us that the tangential acceleration is increasing with time (but it will cut off at t = 2.30 s). From Eq, we write the radial acceleration as
ar=ω2r.
Substituting from Eq. leads us to
ar=(3ct2)2r=9c2t4r
= 9(6.39×10−2rad/s3)2(2.20s)4(33.1m)
= 28.49m/s2≈28.5m/s2,
or 2.9 g (which is also reasonable and a bit exciting).
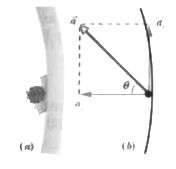
The radial and tangential accelerations are perpendicular to each other and form the components of the rider.s acceleration →a. The magnitude of →a is given by
a=√a2r+a2t
= √(28.49m/s2)2+(27.91m/s2)2
≈39.9m/s2.
or 4.1 g (which is really exciting). All these values are acceptable.
To find the orientation of →a, we can calculate the angle θ shown in Fig.
tanθ=atar.
However, instead of substituting our numerical results, let.s use the algebraic results from Eq.
θ=tan−1(6ctr9c2t4r)=tan−1(23ct3).
The big advantage of solving for the angle algebraically is that we can then see that the angle (1) does not depend on the ring.s radius and (2) decreases as t goes from 0 to 2.20 s. That is, the acceleration vector →a swings toward being radially inward because the radial acceleration (which depends on t4) quickly dominates over the tangential acceleration (which depends on only t). At our given time t = 2.20 s, we have
θ=tan−123(6.39×10−2rad/s3)(2.20s)3=44.4∘.
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - CHECKPOINT
18 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PROBLEMS
100 Videos
- RELATIVITYBOOK - RESNICK AND HALLIDAYCHAPTER - RELATIVITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
5 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
2 Videos
Similar Questions
The angular position of a swinging door is described by θ=5+10t+20t2. Determine the angular position, angular speed and angular acceleration at t=2s.
View SolutionA wheel rotates around a stationary axis so that the rotation angle θ varies with time as θ=2t2 radian. Find the total acceleration of the point A at the rim at the moment t=0.5s If the radius of wheel is 1m.
View Solution
Knowledge Check
The position of a body moving along x-axis at time t is given by x=(t2−4t+6)m. The distance travelled by body in time interval t = 0 to t = 3 s is
A5 mB7 mC4 mD3 mA horizontal disc rotates freely about a vertical axis through its centre. A ring, having the same mass and radius as the disc, is now gently placed on the disc. After some time, the two rotate with a common angular velocity, then
Asome friction exists between the disc and the ringBthe angular momentum of the 'disc plus ring' is conservedCthe final common angular velocity is (23)rd of the initial angular velocity of the discD(23)rd of the initial kinetic energy changes to heatA ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png) Ag√3B2g√3rC√3grDgr
Ag√3B2g√3rC√3grDgr
The angular position of a point on the rim of a rotating wheel is given by θ=4t3−2t2+5t+3 rad. Find
(a) the angular velocity at t=1s,
(b) the angular acceleration at t=2s.
(c ) the average angular velocity in time interval t=0 to t=2s and
(d) the average angular acceleration in time interval t=1 to t=3s.
View SolutionA charge q is placed at the point P as shown in figure on the axis of the ring of elemental thickness 't' and radius R then flux through the ring is :-
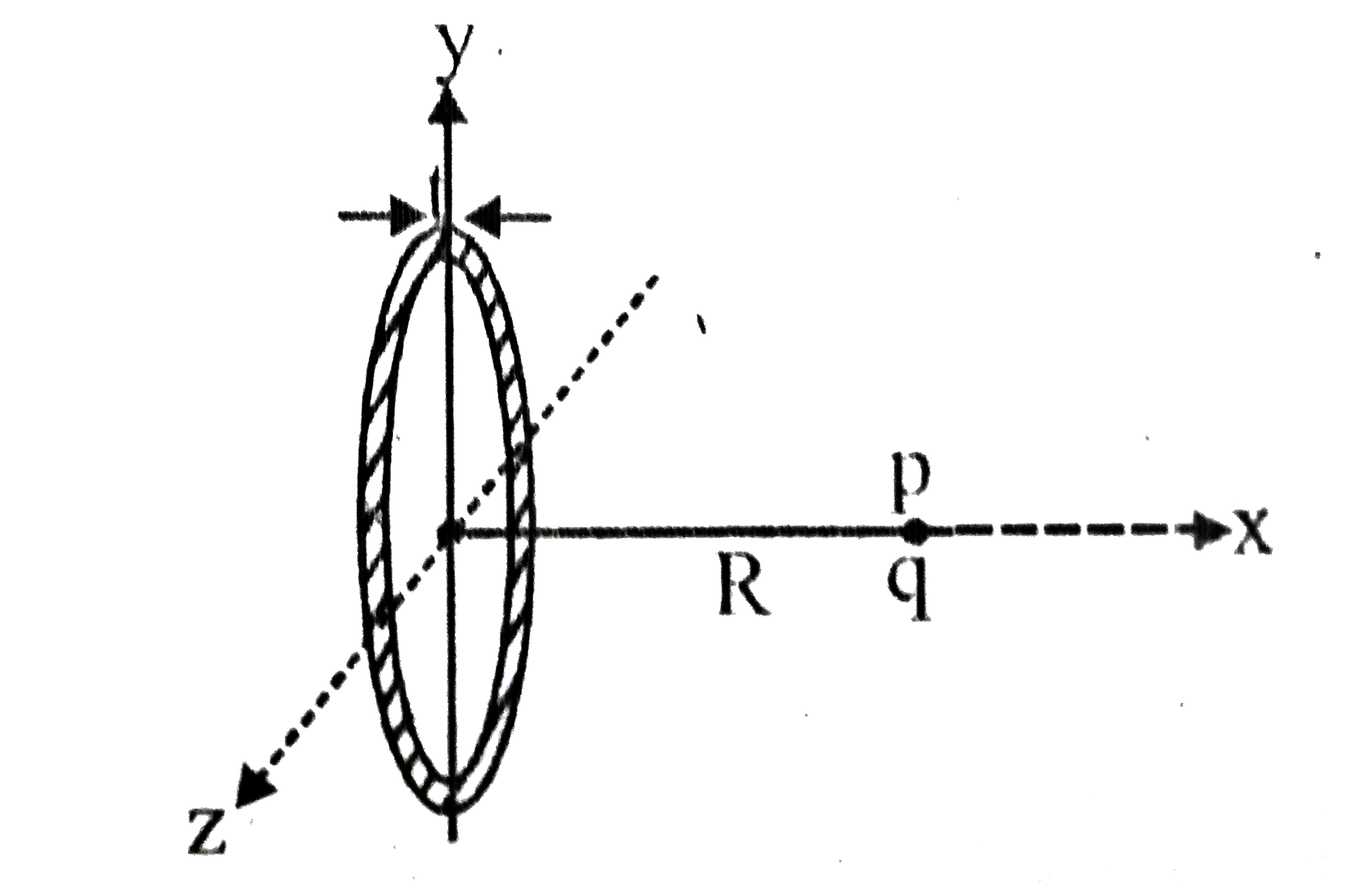
View SolutionA charge q is placed at the point P as shown in figure on the axis of the ring of elemental thickness 't' and radius R then flux through the ring is :-

View SolutionA ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
View SolutionA ring of radius r is rotating about a vertical axis along its diameter with constant angular velocity ω.A read of mass m remains at rest w.r.t. ring at the position shown in figure. Then w2 is:
_2019_CBT8_E01_015_Q01.png)
View Solution
