A rod of mass M and length L lying horizontally is free to rotate about a vertical axis through its end. A horizontal force F on the rod at the other end, the force always remains perpendicular to the rod. Find the angular velocity of the rod when it has turned an angle π/2.
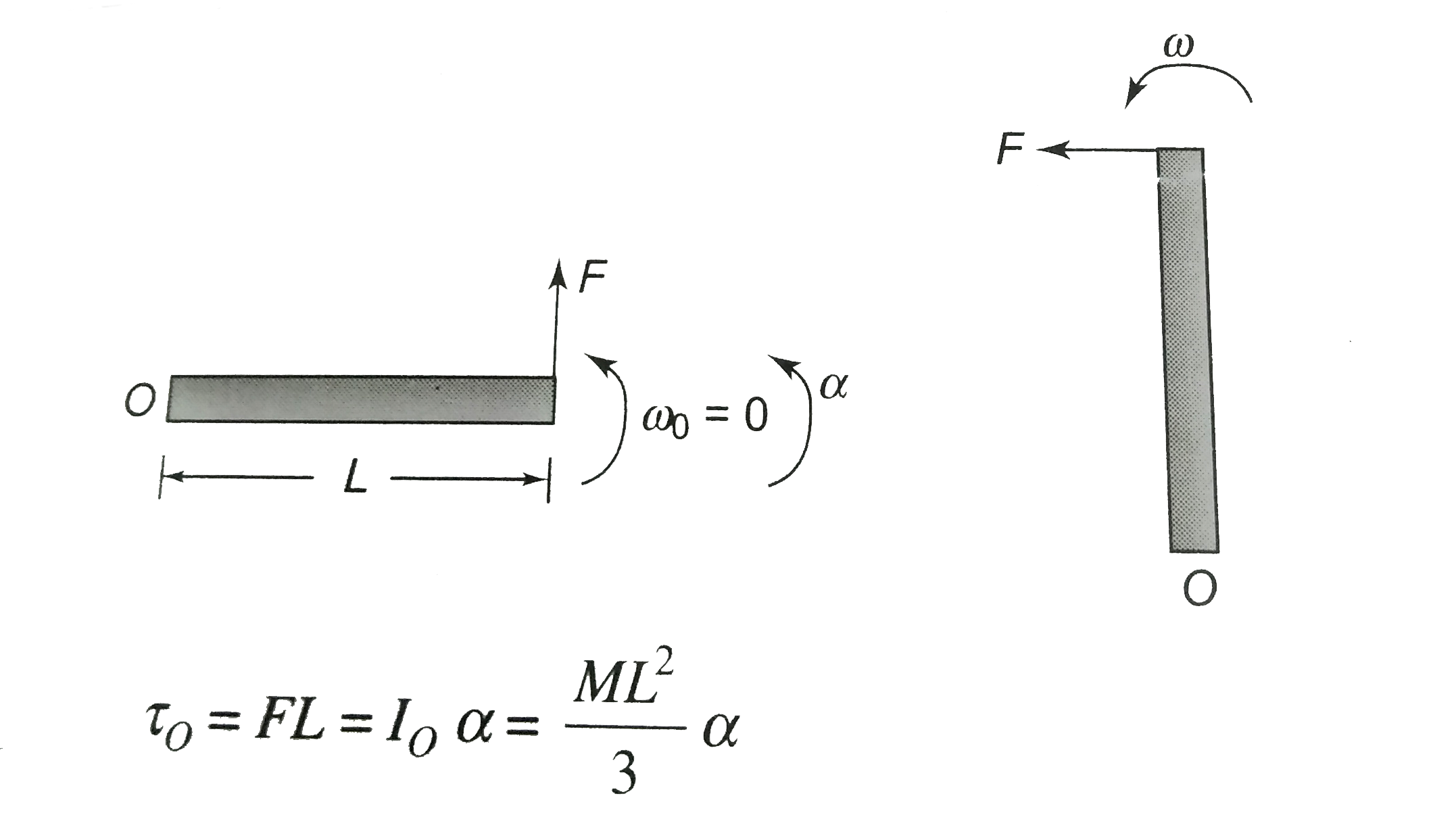
τo=FL=I0α=ML23α
Angular acceleration α=3FML (constant)
ω2=ω20+2αθ
=0+2×3FML×π2
ω=√3πFML
Topper's Solved these Questions
Similar Questions
A rod of mass m and length L , lying horizontally ils free to rotate about a vertical axis through its centre. A horizontal force of constant magnitude LF acts on the rod at a distance of L/4 frm the centre. The force is always perpendicular to the rod. Find the angle rotated by the rod during the time t after the motion starts.
View SolutionA conducting square loop of side length a is held vertical with the help of a non conducting rod of length L. The rod is made to rotate in horizontal circle about a vertical axis through its end. The loop rotates with the rod while its plane always remains perpendicular to the rod. The resistance of the loop is R and angu- lar speed of the rod is ω. There is a uniform horizontal magnetic field B in the entire space. Find the average rate of heat dissipation in the loop during one rotation.
View Solution
Knowledge Check
A thin bar of mass M and length L is free to rotate about a fixed horizontal axis through a point at its end. The bar is brought to a horizontal position and then released. The axis is perpendicular to the rod. The angular velocity when it reaches the lowest point is
Adirectly proportional to its length and inversely proportional to its massBindependent of mass and inversely proportional to the square root of its lengthCdependent only upon the acceleration due to gravity and the length of the barDdirectly proportional to its length and inversely proportional to the acceleration due to gravityA thin horizontal uniform rod AB of mass m and length l can rotate freely about a vertical axis passing through its end A. At a certain moment, the end B starts experiencing a constant force F which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. The angular velocity of the rod as a function of its rotation angle θ measured relative to the initial position should be.
A√6FsinθmlB√2FsinθmlC√3FsinθmlD√5FsinθmlA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]
A thin horizontal uniform rod AB of mass m and length l can rotate freely about a vertical axis passing through its end A. At a certain moment, the end B starts experiencing constant force F which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. Find the angular velocity of the rod as a function of its rotation angle ϕ counted relative to the initial position.
View SolutionA thin horizontal uniform rod AB of mass m and length l can rotate freely about a vertical axis passing through its end A. At a certain moment the end B starts experiencing a constant force F which is always perpendicular to the original position of the stationary rod and directed in a horizonatal plane. Find the angular velocity of the rod as a function of its rotation angle φ counted relative to the initial position.
View SolutionA rod of mass 12 m and length l lying on a smooth horizontal plane can rotate freely about a stationary, vertical axis passing through the rod's end. A particle of mass m moving along the plane with speed v0 hits the rod's end perpendicularly and gets stuck there. Find the angular velocity of the system.

View SolutionA slender rod of mass M and length L rests on a horizontal frictionless surface. The rod is pivoted about one of ends. The impulse of the force exerted on the rod by the pivot when the rod is struck by a blow of impulse J perpendicular to the rod at other end is
View SolutionA uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
View Solution
