A thin horizontal uniform rod $A B$ of mass $m$ and length $l$ can rotate freely about a vertical axis passing through its end $A$ . At a certain moment, the end $B$ starts experiencing constant force $F$ which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. Find the angular velocity of the rod as a function of its rotation angle $ϕ$ counted relative to the initial position.

Video Solution

Text Solution

Verified by Experts

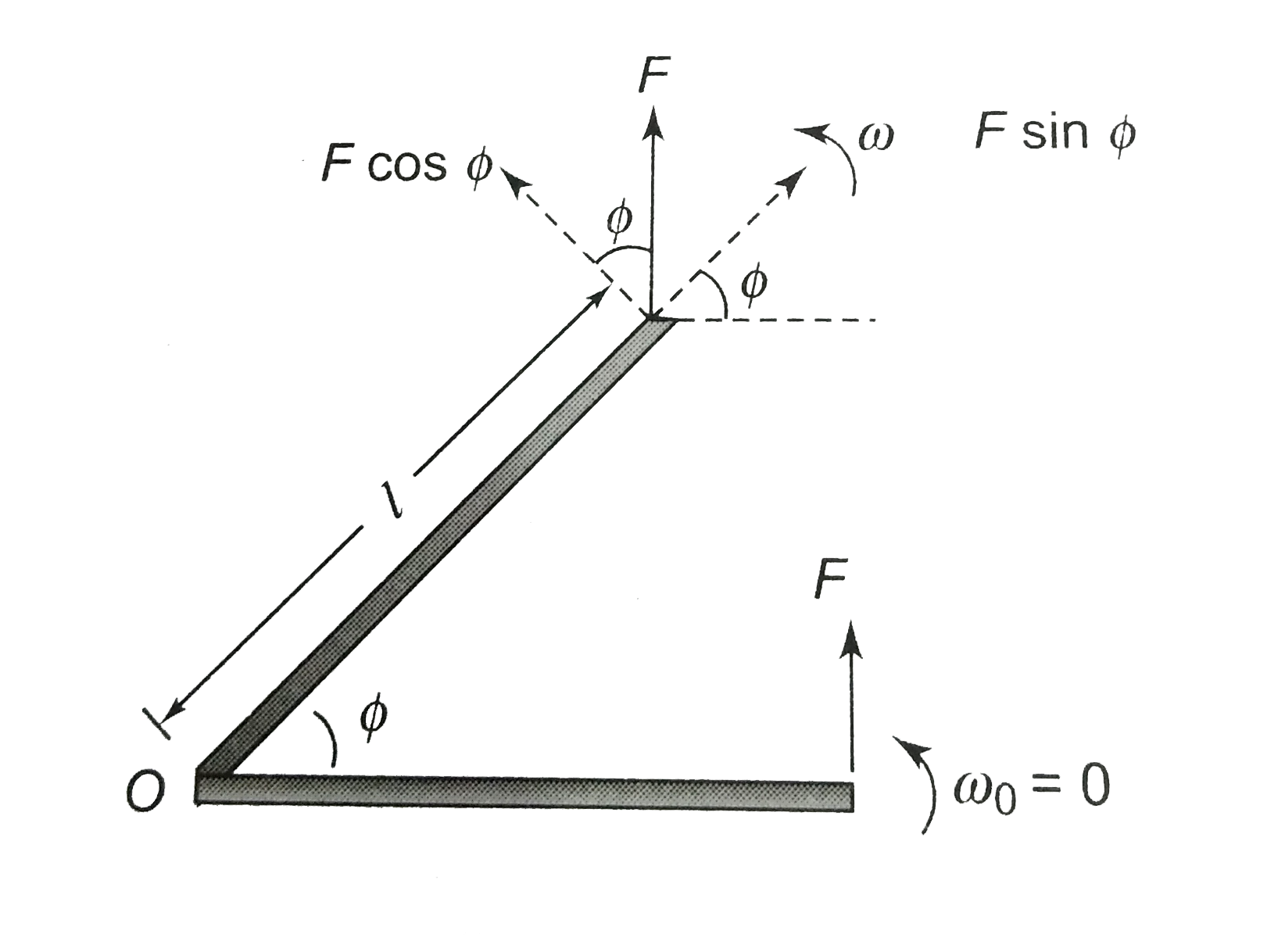
$τ_{o} = F cos ϕ l = I_{0} α = \frac{m l^{2}}{3} α$
$α = \frac{3 F cos ϕ}{m l}$ (variable angular acceleration)
$ω \frac{d ω}{d ϕ} = \frac{3 F cos ϕ}{m l}$
$\int_{0}^{ω} ω d ω = \frac{3 F}{m l} \int_{0}^{ω} cos ϕ d ϕ$
$\frac{ω^{2}}{2} = \frac{3 F}{m l} sin ϕ \Rightarrow \sqrt{\frac{6 f sin ϕ}{m l}}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A thin horizontal uniform rod $A B$ of mass $m$ and length $l$ can rotate freely about a vertical axis passing through its end $A$ . At a certain moment, the end $B$ starts experiencing a constant force $F$ which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. The angular velocity of the rod as a function of its rotation angle $θ$ measured relative to the initial position should be.
A $\sqrt{\frac{6 F sin θ}{m l}}$
B $\sqrt{\frac{2 F sin θ}{m l}}$
C $\sqrt{\frac{3 F sin θ}{m l}}$
D $\sqrt{\frac{5 F sin θ}{m l}}$
Question 2 - Select One
A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A $\frac{1}{2} m ω^{2} x$
B $\frac{1}{2} m ω^{2} (1 - \frac{x^{2}}{l})$
C $\frac{1}{2} m ω^{2} l (1 - \frac{x^{2}}{l^{2}})$
D $\frac{1}{2} m ω^{2} l [1 - \frac{x}{l}]$
Question 3 - Select One
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all points
Bdifferent at differen points and maximum at centre of rod
Cdifferent at different points and minimum at axis of rotation.
Ddifferent at different points and maximum at axis of rotation

CP SINGH-ROTATIONAL MOTION-Exercise

Home
Ask Doubt
Profile