Consider the situation as shown in the figure. If m1>m2, I is the moment of intertia about its axis of rotation, R is the radius of pulley. The objects are released from rest separated by a vertical distance 2h. Find the translational speed of the objects as they pass each other. Assume no slipping.
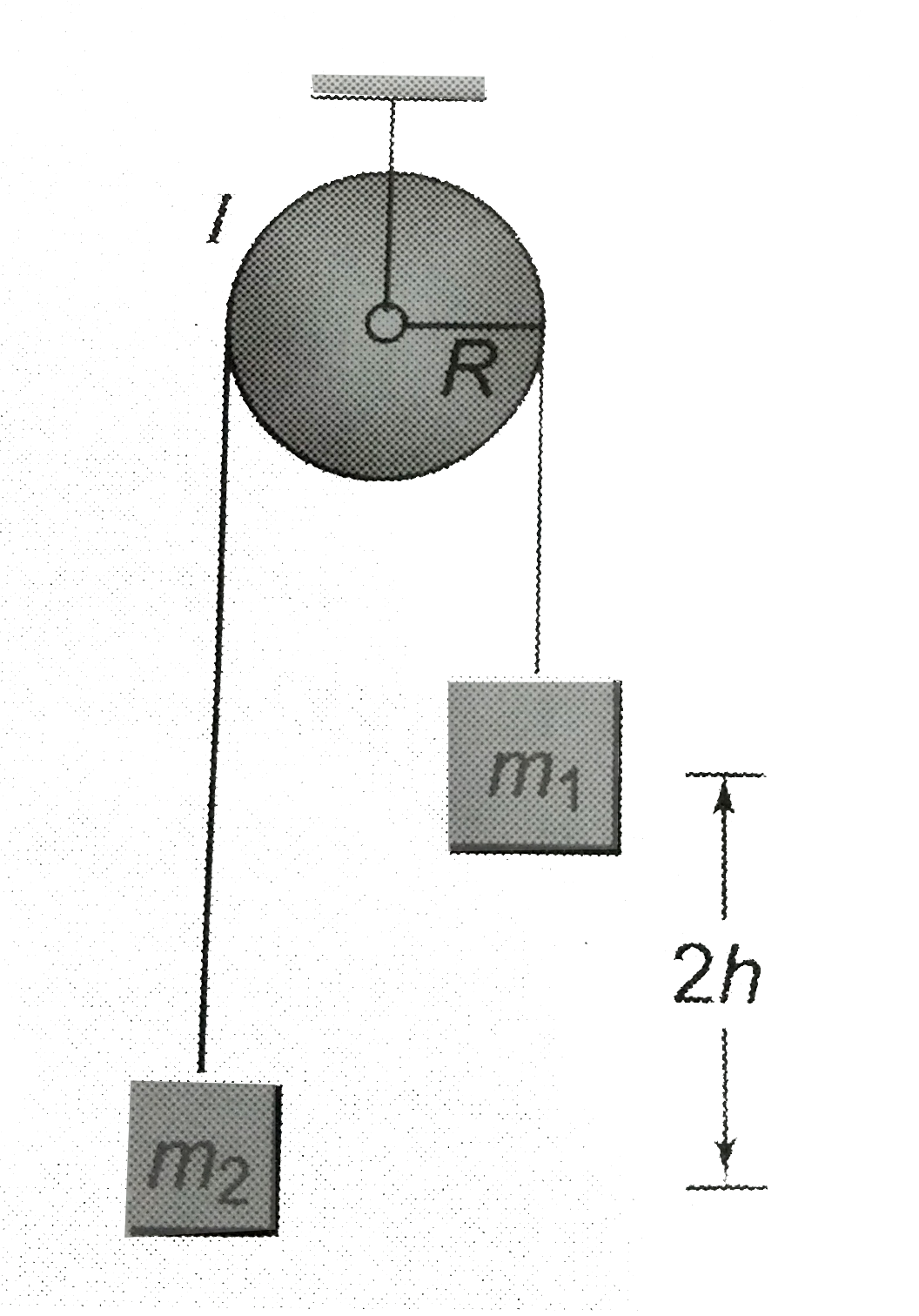
When objects cross each other, their speed is same, the angular speed of pulley is ω.
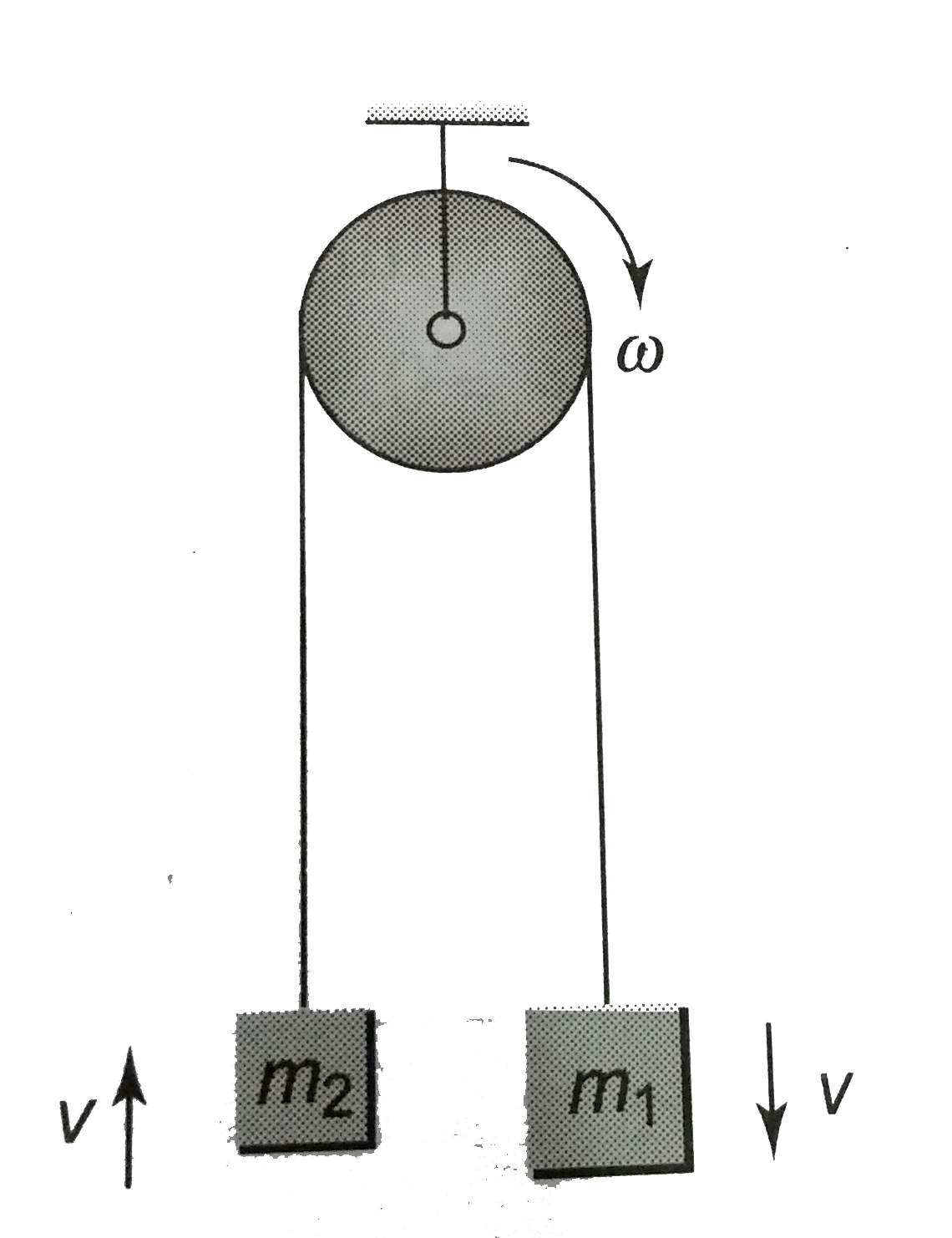
The block of mass m1 has gone down by h, block of mass m2 has gone up by h.
Loss in the gravitational potential energy of m1
= gain in gravitational potential energy of m2
+ gain kinetic energy of (block + pulley)
m1gh=m2gh+12m1v2+12m2v2+12Iω2
(m1−m2)gh=12(m1+m2+IR2)v2[ω=vR]
v=
⎷2(m1−m2)ghm1+m2+IR2
Topper's Solved these Questions
Similar Questions
Consider the situation as shown in the figure. The pulley has moment of inertia I and radius r. The table is rough and the coefficient of kinetic friction is μk. The system is released from the rest. Calculated speed of block of mass 3m as a function of the distance h it has descended. Assume no slipping.

View SolutionConsider the situation as shown in the figure. The moment of inertia of wheel is 2kgm2 and its radius is 0.25m. Find the angular acceleration of the wheel, assuming no slipping.

View Solution
Knowledge Check
Consider two object with m1>m2 connected by a light string that passes over a pulley having a moment of inertia of I about its axis of rotation as shown in figure. The string does not slip on the pulley or strech. The pulley turns without friction. The two objects are released from rest separated by a vertical distance 2h. The translational speeds of the objects as they pass each other is.
 .A ⎷2(m1+m2)ghm1+m2+IR2B ⎷2(m1−m2)ghm1+m2+IR2C ⎷(m1−m2)ghm1+m2+IR2D ⎷(m1+m2)ghm1+m2+IR2
.A ⎷2(m1+m2)ghm1+m2+IR2B ⎷2(m1−m2)ghm1+m2+IR2C ⎷(m1−m2)ghm1+m2+IR2D ⎷(m1+m2)ghm1+m2+IR2Consider two masses with m1>m2 connected by a light inextensible string that passes over a pulley of radius R and moment of inertia I about its axis of rotation. The string does not slip on the pulley and the pulley turns without friction. The two masses are released from rest separated by a vertical distance 2h. When the two masses pass each other, the speed of the masses is proportional to
A ⎷m1−m2m1+m2+1R2B ⎷(m1−m2)(m1−m2)m1+m2+1R2C ⎷m1+m2+1R2m1−m2D ⎷1R2m1+m2Two objects of masses 1kg and 2kg separated by a distance of 1.2m are rotating about their centre of mass. Find the moment of inertia of the system
A0.96kgm2B0.48kgm2C0.83kgm2D0.72kgm2
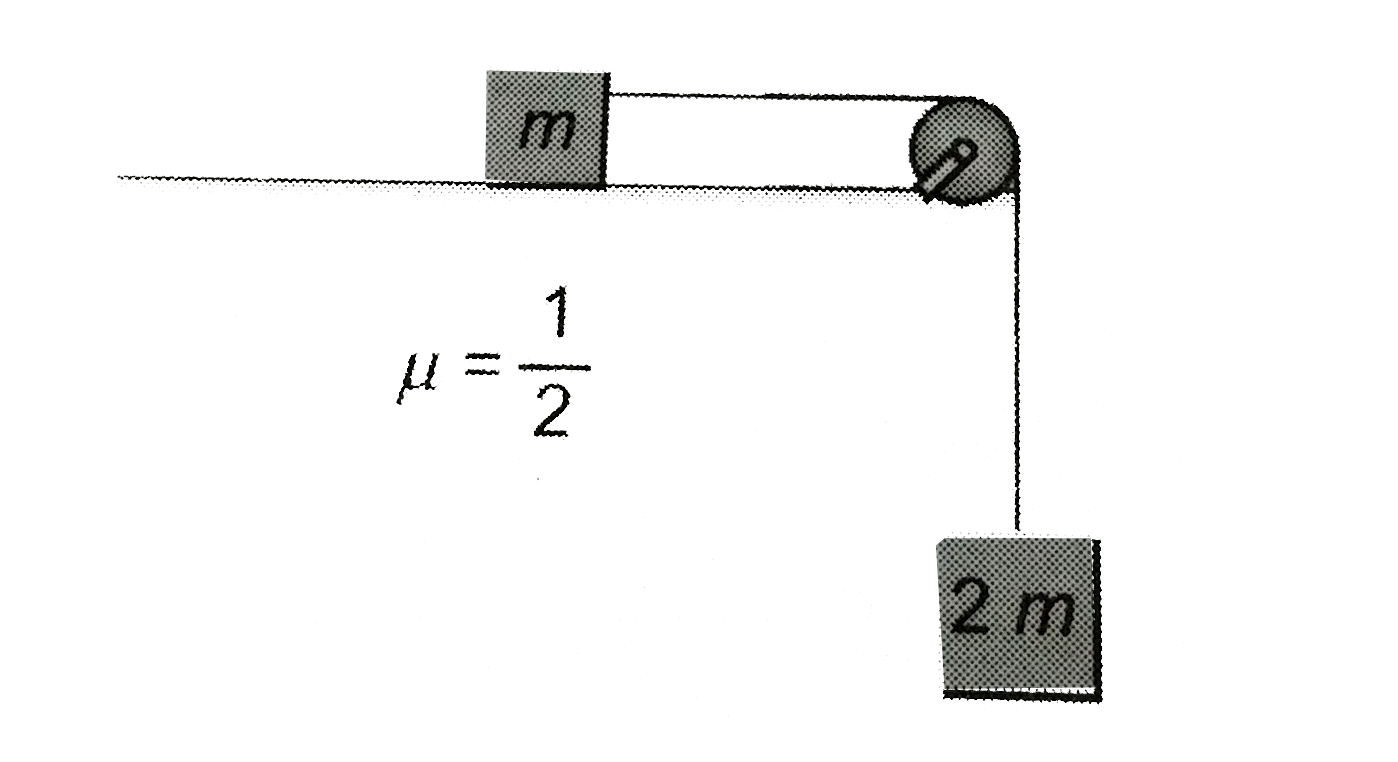
Consider the situation as shown in the figure. The system is released from rest. Find the speed of m when it has traveled a distance d on a rough surface.
View SolutionThe mass of a thin circular plate is M and its radius is R. About an axis in the plane of plate at a perpendicular distance R/2 from centre of plate, its moment of inertia is
View SolutionA wheel of moment of inertial I and radius R is rotating about its axis at an angular speed ω. It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.
View SolutionConsider the situation as shown. The pulley has a moment of inertia I, and radius r, the block is in equilibrium. Find the time period of mass m. Assume no slipping.

View SolutionConsider the situation as shown in the diagram. The pulley has radius R and moment of inertia I. The block is release when the spring (spring constant k) is unstretched. Find the speed of block when the vlock has fallen a distance h. Assume no slipping.

View Solution
