A light thread with a body of mass m tied to its end is wound on a uniform solid cylinder of mass M and radius R. At a moment t=0 the system is set in motion. Assuming the friction in the axle of the cylinder to be negligible, find the time dependence of
(a) the angular velocity of the cylinder and
(b) the kinetic energy of the whole system ( M=2m).

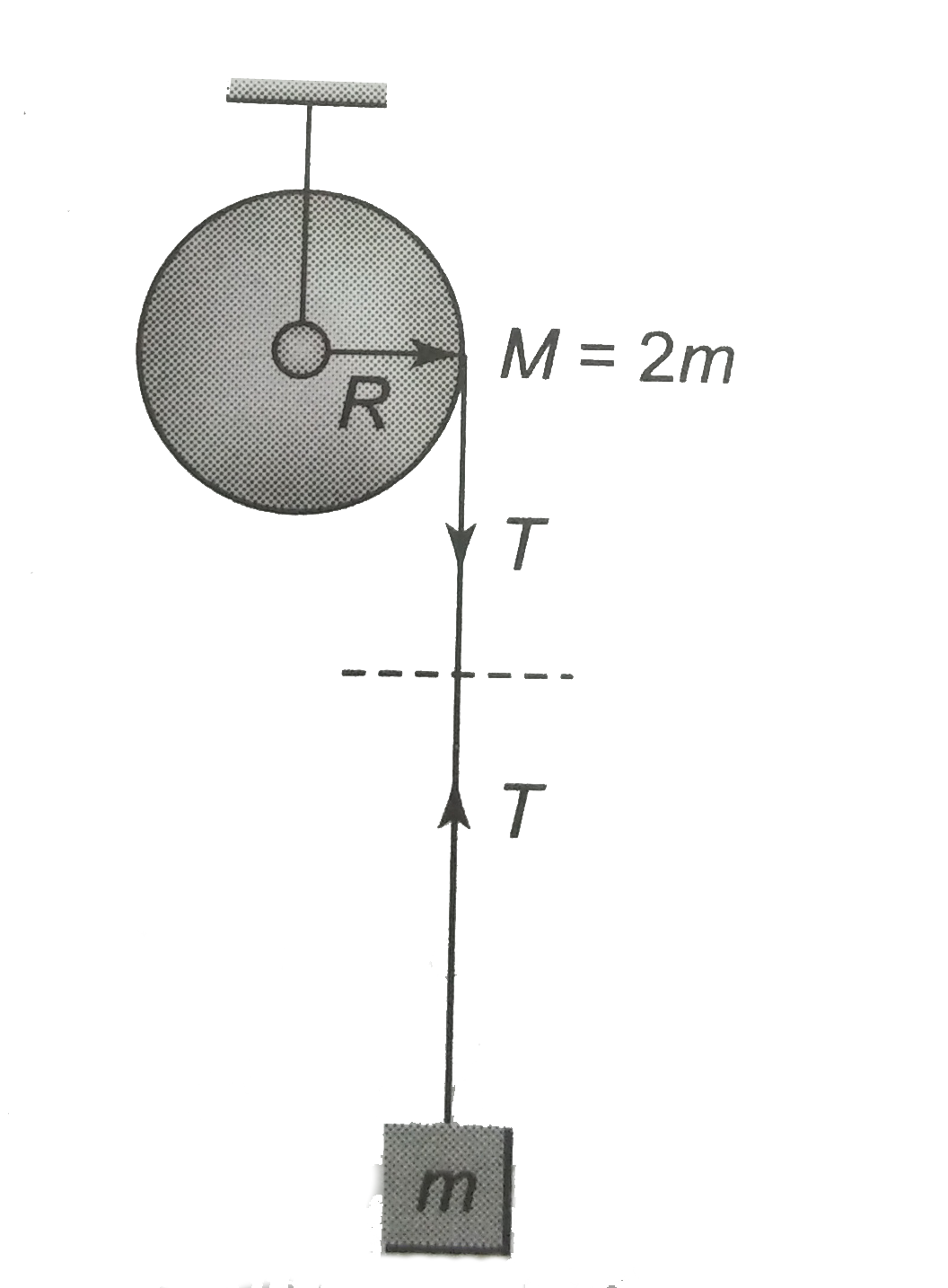
Linear motion of the block:

mg−T=ma (i)
Angular motion of the pulley:
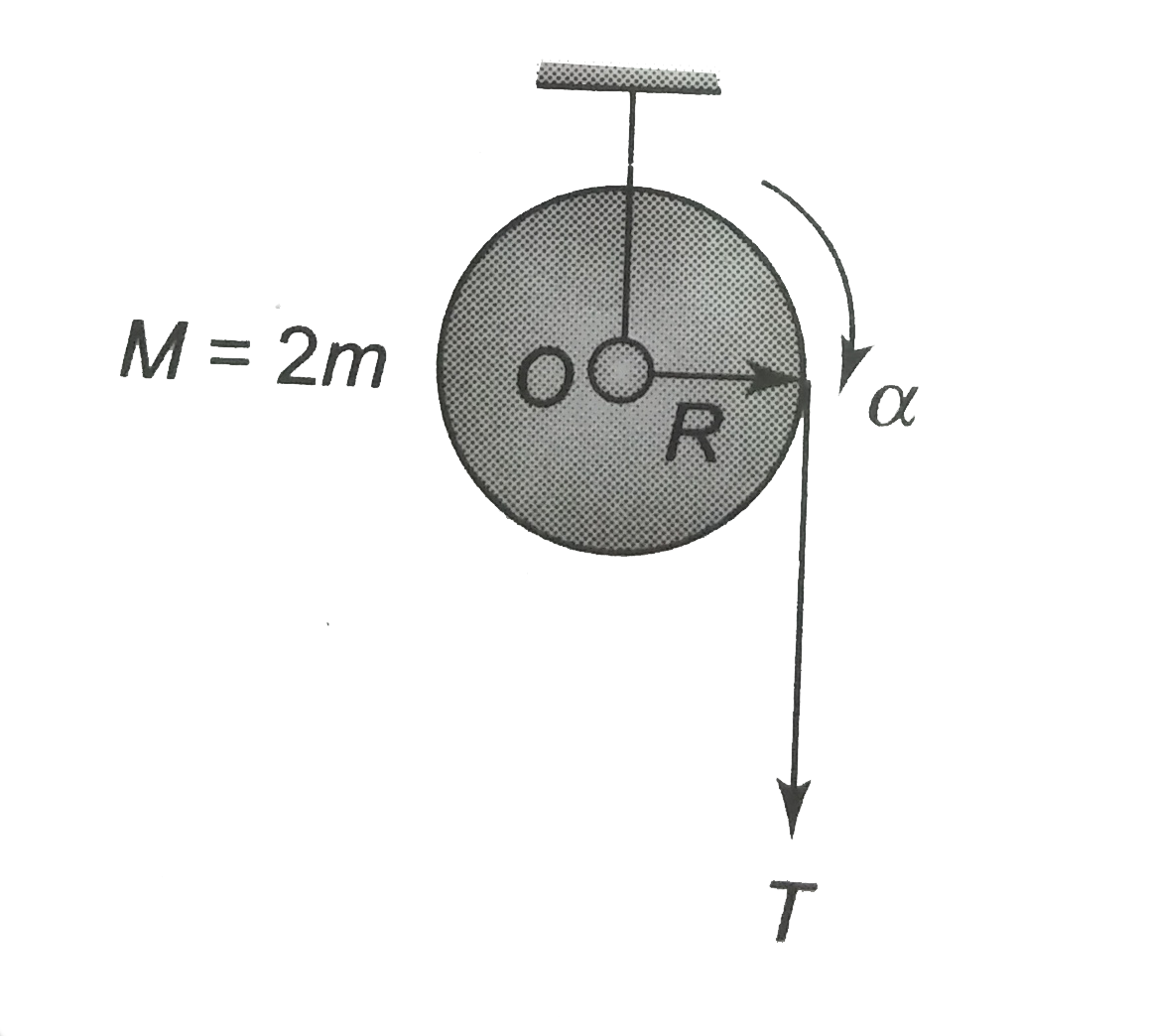
τ0=T×R=I0α
TR=12×2mR2α=mR2α (ii)
a=Rα (iii)
From (ii) and (iii), T=ma
mg−T=ma⇒mg−ma=ma⇒a=g2
α=aR=g2R
Angular velocity of cylinder after time t
ω=ω0+αt=0+gt2R=gt2R
K.E. of system =K.E. of block +K.E. of pulley
=12mv2+12I0ω2
=12mR2ω2+12×12×2mR2ω2
=mR2ω2=mR2(gt2R)2
=14mg2t2
Topper's Solved these Questions
Similar Questions
In the following figure, a body of mass m is tied at one end of a light string and this string is wrapped around the solid cylinder of mass M and radius R. At the moment t = 0 the system starts moving. If the friction is negligible, angular velocity at time t would be
 View Solution
View SolutionThread would around cylinder of mass M and radius R. It is allowed to fall as shown. Find its acceleration.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Moment of inertia of a hollow cylinder of mass M and radius R, about the axis of cylinder is
A12MR2BMR2C23MR2D25MR2 - Question 2 - Select One
In the following figure, a body of mass m is tied at one end of a light string and this string is wrapped around the solid cylinder of mass M and radius R. At the moment t = 0 the system starts moving. If the friction is negligible, angular velocity at time t would be
 AmgRt(M+m)B2Mgt(M+2m)C2mgtR(M−2m)D2mgtR(M+2m)
AmgRt(M+m)B2Mgt(M+2m)C2mgtR(M−2m)D2mgtR(M+2m) - Question 3 - Select One
A rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be
AMRFBMRFCRMFDFMR
A uniform disc of radius R and mass M is mounted on an axis supported in fixed friction less bearing. A light cord is wrapped around the rim of the wheel and suppose we hang a body of mass m from the cord.
(a) Find the angular acceleration of the disc and tangential acceleration ofpoint on the rim.
(b) At a moment t= 0, the system is set in motion, find the time dependence of the angular velocity of the system and the kinetic energy ofthe whole system.View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionA bullet of mass m moving with a velocity of u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.
 View Solution
View SolutionA rope is wound round a hollow cylinder of mass M and radius R. If the rope is pulled with a force F newton, then the angular acceleration of the cylinder will be
View SolutionA solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
View Solution

