A ball of radius R=10.0cm rolls without slipping down an inclined plane so that its centre moves with constant acceleration
w=2.50cm/s2, t=2.00s after the beginning of motion its position corresponds to that shown in figure. Find:
(a) the velocities of the points A, B, and O,
(b) the accelerations of these points.

Linear motion: velocity of center of mass after time t
vc=vc.m.=0+ac.m.t=a0t
Angular motion: ω=ω0+αt=0+αt=a0Rt
(In pure rolling, ac.m.=Rα⇒a0=Rα)
Rolling without slipping about center of mass C

(a) 
A: 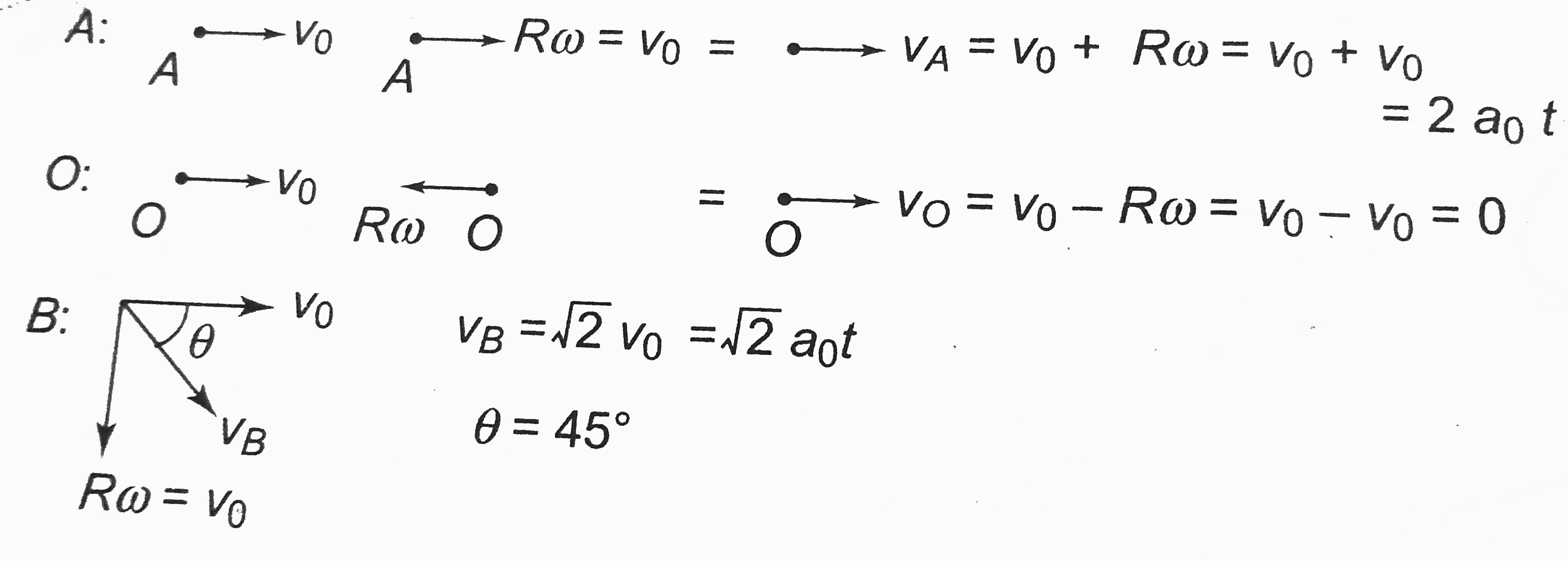 =v0+Rω=v0+v0=2a0t
=v0+Rω=v0+v0=2a0t
O:  =v0−Rω=v0−v0=0
=v0−Rω=v0−v0=0
B:  =vB=√2v0=√a0t
=vB=√2v0=√a0t
θ=45∘
(b) Tangential acceleration:

A: 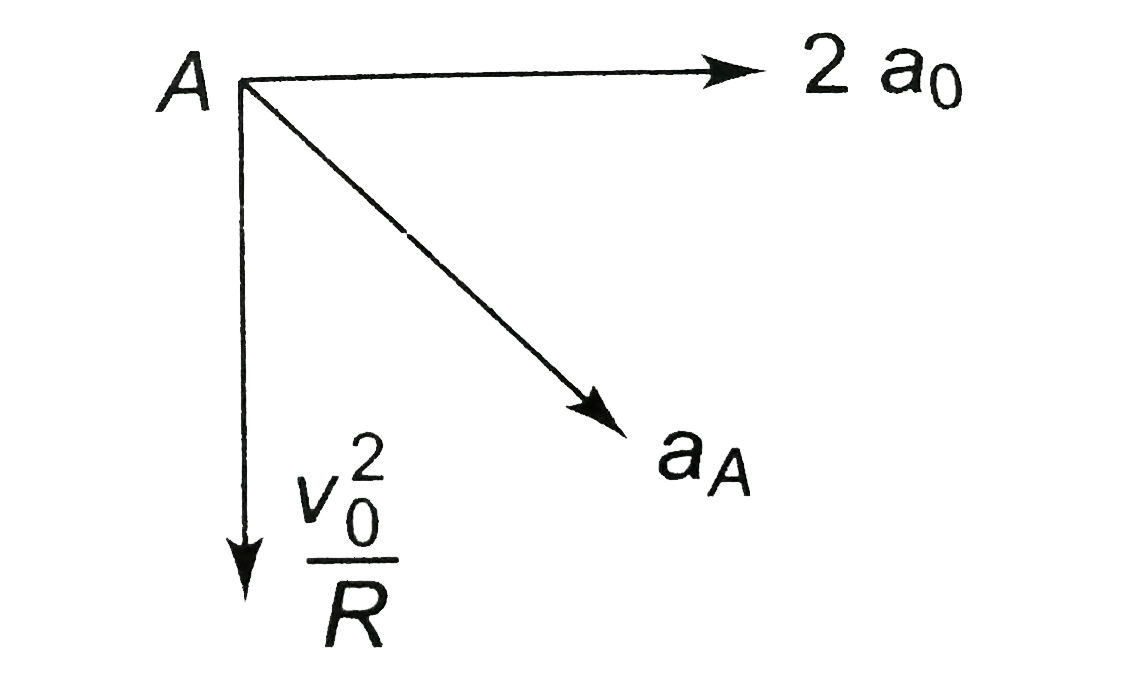 aA=a0+Rα=2a0
aA=a0+Rα=2a0
O:  a0=0
a0=0
O: 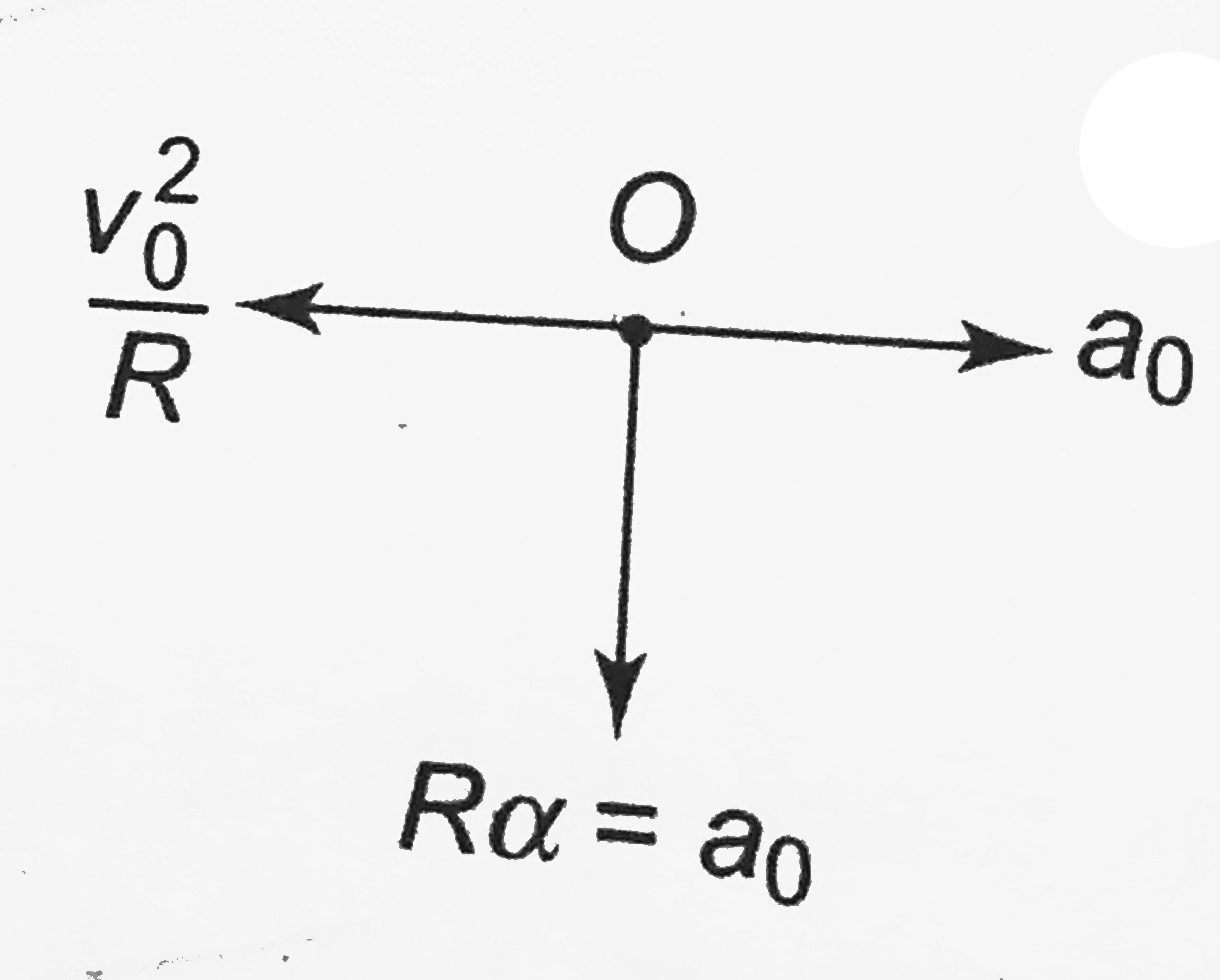 aB=√2a0
aB=√2a0
θ=45∘
Centripetal acceleration

Total acceleration
A: aA=
⎷(2a0)2+(v20R)2=
⎷4a20+(a20t2R)2
O: a0=v20R=a20t2R
B: aB=
⎷a20+(a0−v20R)2=
⎷a20+(a0−a20t2R)2
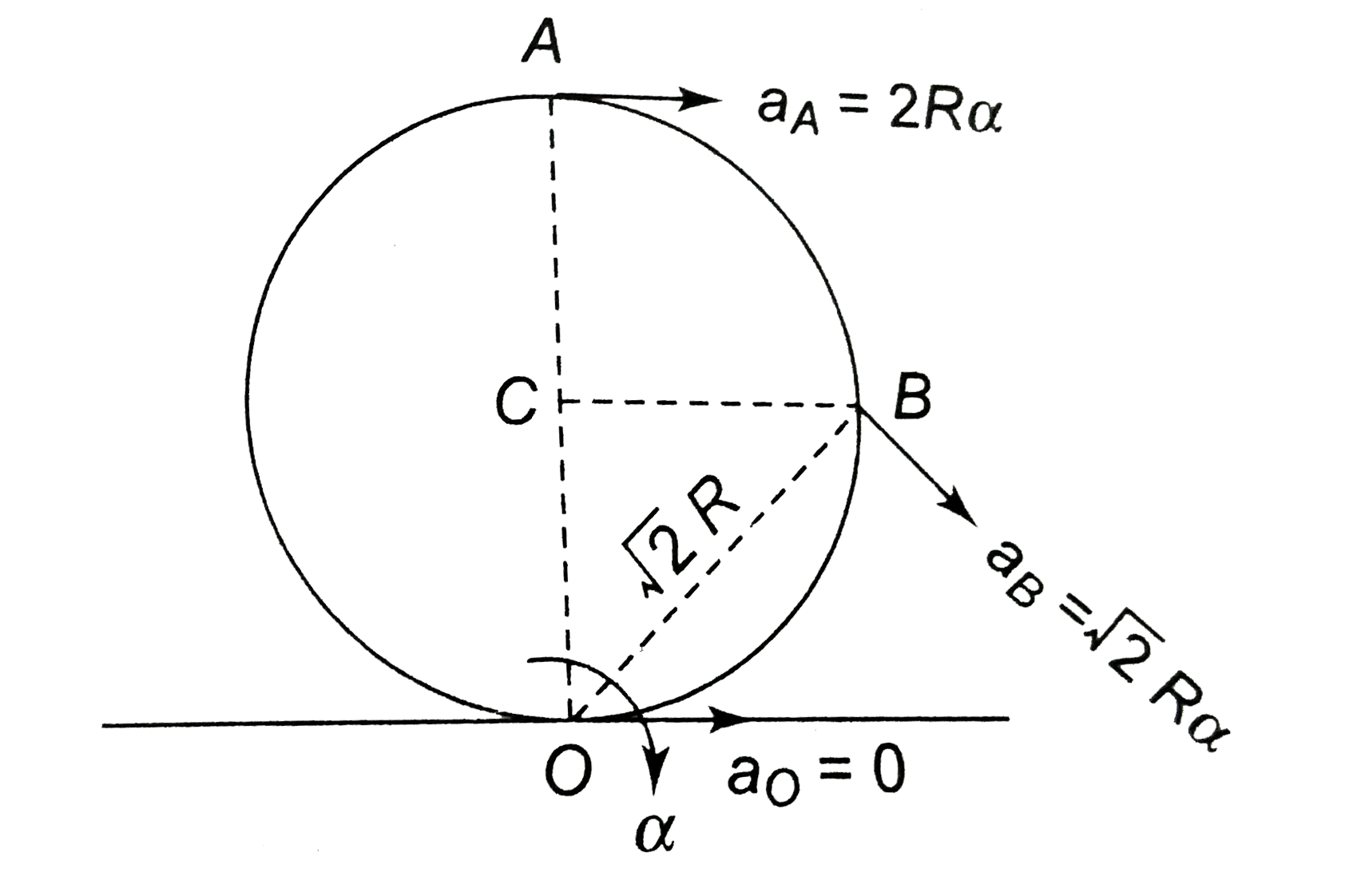
Alternative approach to find velocities and acceleration of points A, B and O:
Rolling without slipping is equivalent to pure rotation at the contact point
vC=Rω=a0t
vA=2Rω=2v0=2a0t
vB=√2Rω=√2v0=√2a0t
vO=0
ac.m.=ac=a0=Rα
aA=2Rα=2a0
aB=√2Rα=√2a0
aO=0
Topper's Solved these Questions
Similar Questions
A uniform sphere of mass 200 g rols withiout slipping on a plane surface so that its centre mioves at a speed of 2.00 cm/s. Find its kinetic energy.
View SolutionConsider a wheel rolls without slipping and its centre moves with constant acceleration a. Find the acceleration of points O,P,Q and S when linear velocity of the centre of wheel is v.
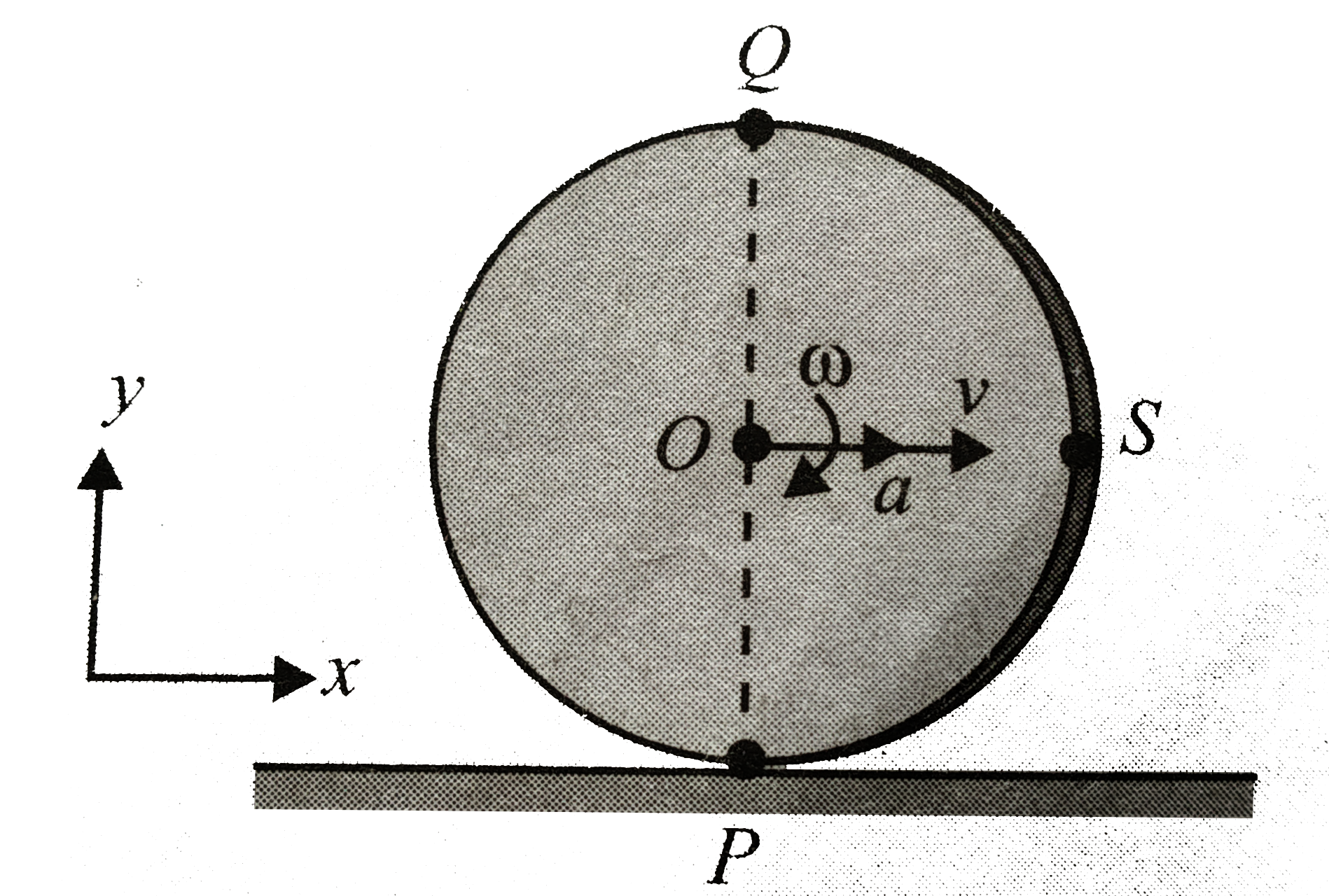 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A wheel of radius R=0.1m is rolling without slipping on a horizontal surface as shown in the firgure. Centre of the wheel moves with a constant speed √3m/s. The speed of the point P with respect to ground is
 A2√3m/sBzeroC3 m/sD√3m/s
A2√3m/sBzeroC3 m/sD√3m/s - Question 2 - Select One
A uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
A4.17×10−4JB8.72×10−3JC6.25×10−4JD3.61×10−4J - Question 3 - Select One
A uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
A4×10−3JB8×10−3JC3.33×10−3JD3.5×10−3J
A trolley, while going down an inclined plane, has an acceleration of 2cm/s2 starting from rest. What will be its velocity 3s after the start ?
View SolutionA particle moves with deceleration along a circle of radius R so that at any moment its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v0. Find (a) the velocity of the point as a function of t and s , (b) the resultant acceleration modulus as a function of v.
View Solution(a) A rigid body of radius of gyration k and radius R rolls without slipping down a plane inclined at an angle θ with the horizontal. Calculate its acceleration and the frictional force acting on it.
(b) If the body be in the form of a disc and θ=30∘, what will be the acceleration and the frictional force acting on it.View SolutionAt t = 0, block B in figure starts moving with a velocity 15 cm/s and with a constant acceleration. It is observed that after blocks travels 24 cm to the right its velocity is 6cm/s. Find:
(a) The accelerations of A and B,
(b) The acceleration of point M of the string.View SolutionAn object is sliding down an inclined plane. The velocity changes at a constant rate from 10 cm/s to 15 cm/s in two seconds. What is its acceleration ?
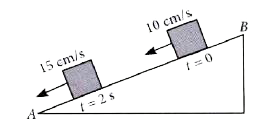 View Solution
View Solution

