A car is moving on a circular path and takes a turn. If R1 and R2 be the reactions on the inner and outer wheels, respectively, then
R1=R2
R1<R2
R1>R2
R1≥R2
To solve the problem regarding the reactions on the inner and outer wheels of a car moving on a circular path, we can analyze the forces acting on the car as it takes a turn.
1. Understanding the Forces: When a car moves in a circular path, it experiences centripetal force directed towards the center of the circle. The frictional force between the tires and the road provides this centripetal force.
2. Identifying the Wheels: The car has two sets of wheels: the inner wheels (on the side of the turn) and the outer wheels (on the opposite side). The reactions on these wheels, denoted as R1 (inner wheel) and R2 (outer wheel), will differ due to the distribution of weight and the need for centripetal force.
3. Weight Distribution: When the car turns, the weight of the car acts downwards through its center of gravity. The weight is distributed between the inner and outer wheels. The outer wheels will generally bear more weight because they are further from the center of the circular path.
4. Centripetal Force Requirement: For the car to maintain its circular motion, the net force acting towards the center of the circle must equal the required centripetal force. This force is provided by the frictional forces at the wheels.
5. Setting Up the Equations:
- Let W be the total weight of the car.
- The sum of the vertical forces must equal the weight of the car:
R1+R2=W
- The frictional forces at the inner and outer wheels provide the necessary centripetal force:
R2−R1=Centripetal Force
6. Solving the Equations: From the two equations above, we can solve for R1 and R2:
- Rearranging the second equation gives us:
R2=R1+Centripetal Force
- Substituting R2 into the first equation:
R1+(R1+Centripetal Force)=W
2R1+Centripetal Force=W
- Solving for R1:
R1=W−Centripetal Force2
- Then substituting R1 back to find R2:
R2=W+Centripetal Force2
Final Result:
The reactions on the inner and outer wheels can be expressed as:
- R1=W−Centripetal Force2
- R2=W+Centripetal Force2
- Let W be the total weight of the car.
- The sum of the vertical forces must equal the weight of the car:
R1+R2=W
- The frictional forces at the inner and outer wheels provide the necessary centripetal force:
R2−R1=Centripetal Force
- Rearranging the second equation gives us:
R2=R1+Centripetal Force
- Substituting R2 into the first equation:
R1+(R1+Centripetal Force)=W
2R1+Centripetal Force=W
- Solving for R1:
R1=W−Centripetal Force2
- Then substituting R1 back to find R2:
R2=W+Centripetal Force2
The reactions on the inner and outer wheels can be expressed as:
- R1=W−Centripetal Force2
- R2=W+Centripetal Force2
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A car is moving on a circular path and takes a turn. If R1 and R2 be the reaction on the inner and outer wheels respectively, then
AR1=R2BR1<R2CR1>R2DR1≥R2 - Question 2 - Select One or More
The centre of gravity of a car is at a height h and the distance between its wheel is 2a. The car moves on a level curve of radius r with speed v. Let N1andN2 be the normal reactions on the inner and outer wheels of the car. Then
AN1>N2BN2>N1CN1=N2Dthe maximum value of v to avoid overturning is √argh - Question 3 - Select One
When a car negotiates a curve, the normal force exerted on the inner and outer wheels are N2 and N1 respectively. Then N1/N2 is
A=1B<1C>1Dzero
A car of mass m travelling at speed v moves on a horizontal track. The centre of mass of the car describes a circle of radius r. If 2a is the separation of the inner and outer wheels and h is the height of the centre of mass above the ground, show that the limiting speed beyond which the car will overturn in given by
v2=grah
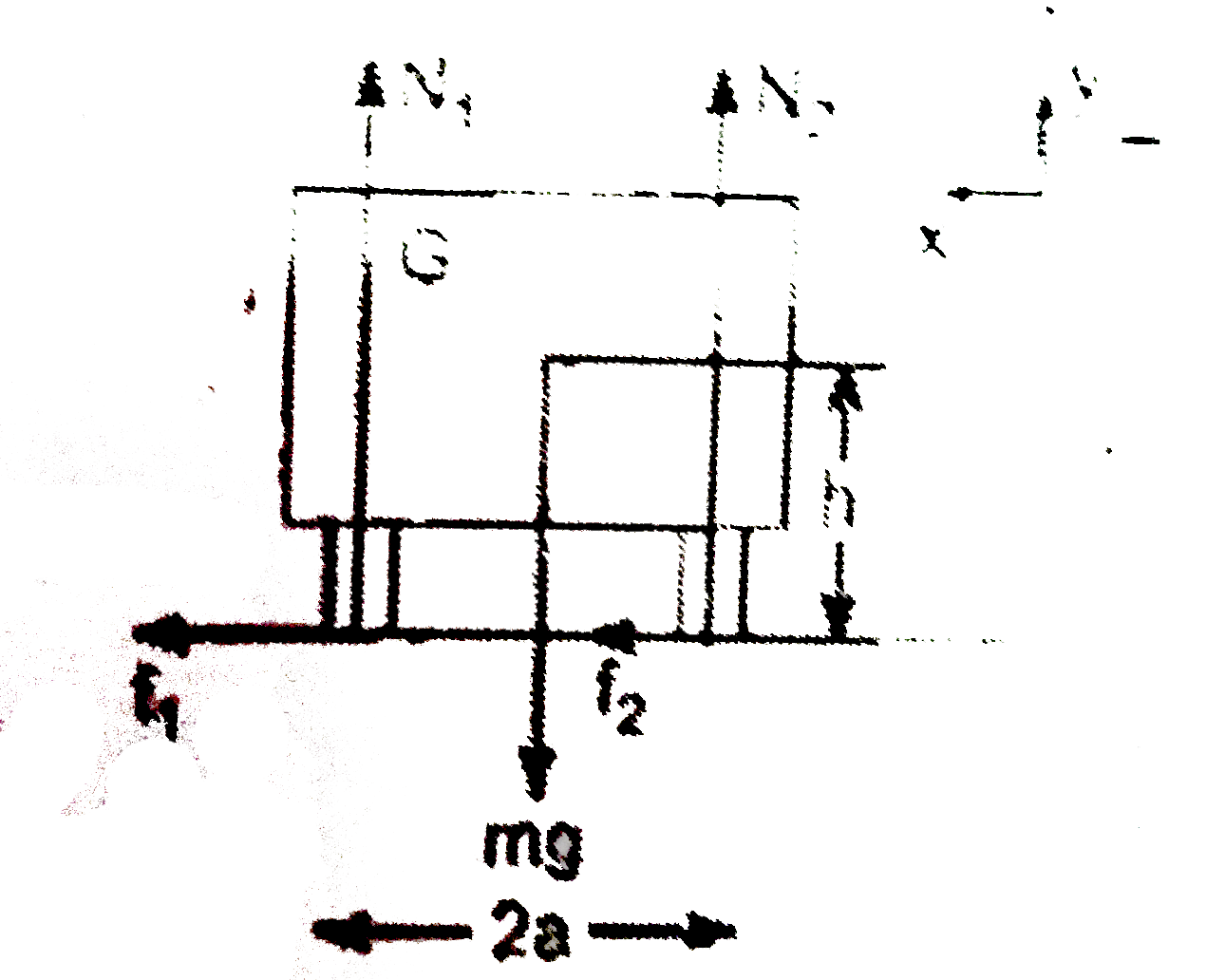 View Solution
View SolutionA particle is moving around a circular path with uniform angular speed (x) . The radius of the circular path is (r). The acceleration of the particle is:
View SolutionA car is moving on a circular road which is rough and banked at angle . If radius of circular track is R then. Choose correct statement:
 View Solution
View SolutionA car is taking turn on a circular path of radius R. If the coefficient of friction between the tyres and road is μ, the maximum velocity for no slipping is
View SolutionA car moves with speed v on a horizontal circular track of radius R. A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground is h, and the separation between its inner and outer wheels is d The road is dry, and the car does not skid. The maximum speed the car can have without overturning is :
 .View Solution
.View Solution

