A uniform disc of radius r is to be suspended through a small hole made in te disc. Find the minimum possible time period of the disc for small oscillations. What should be the distance of the hole from the centre for it to have minimum time period?

Video Solution

Text Solution

Verified by Experts

Let distance between centre of disc and point of suspension is x.

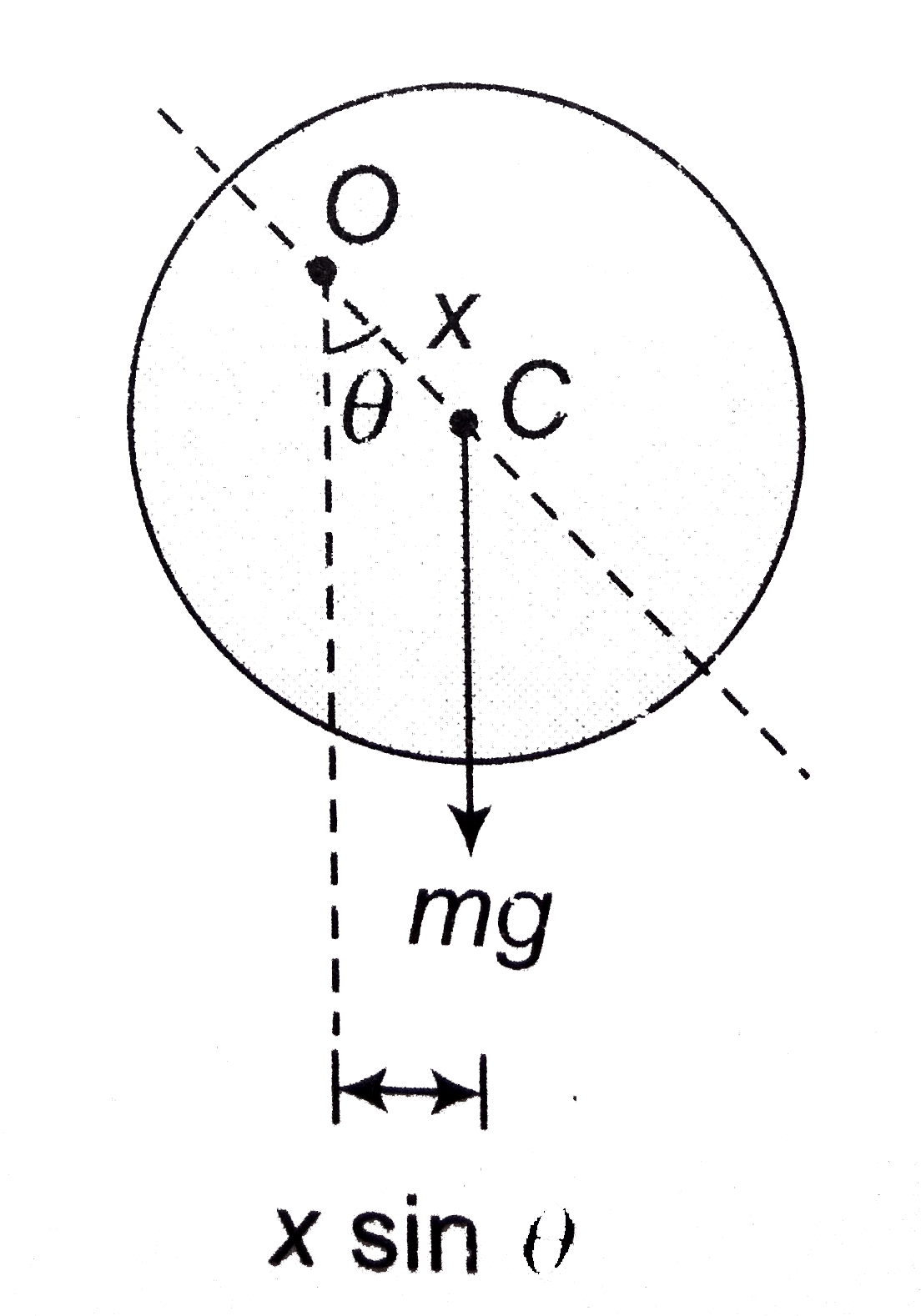
$τ = - m g x sin θ$
$I = \frac{m r^{2}}{2} + m x^{2}$
$τ = - m g x θ$ ( $∵ sin θ = θ$ )
$I α = - m g x θ$
$α = - \frac{m g x}{I} θ = - ω^{2} θ$
$T = 2 π \sqrt{\frac{I}{m g x}} \Rightarrow T^{2} = 4 π^{2} ⎛ ⎜ ⎝ \frac{\frac{m r^{2}}{2} + m x^{2}}{m g x} ⎞ ⎟ ⎠$
$T^{2} = \frac{4 π^{2}}{g} (\frac{r^{2}}{2 x} + x)$
For T to be minimum, $\frac{d T}{d x}$ or $\frac{d (T^{2})}{d x} = 0$
$\frac{d (T^{2})}{d x} = - \frac{r^{2}}{2 x^{2}} + 1 = 0 \Rightarrow x = r / \sqrt{2}$
$T_{min} = {[\frac{4 π^{2}}{g} (\frac{r^{2}}{\sqrt{2} r} + \frac{r}{\sqrt{2}})]}^{\frac{1}{2}} \Rightarrow T_{min} = 2 π \sqrt{\frac{\sqrt{2} r}{g}}$

Updated on:21/07/2023

A disc of radius R is suspended from its circumference and made to oscillate. Its time period will be:
A $2 π \sqrt{\frac{3 R}{2 g}}$
B $2 π \sqrt{\frac{4 R}{g}}$
C $2 π \sqrt{\frac{R}{g}}$
D $2 π \sqrt{\frac{2 R}{g}}$
A uniform disc of radius R is pivoted at point O on its circumstances. The time period of small oscillations about an axis passing through O and perpendicular to plane of disc will be
A $2 π (\frac{R}{g})$
B $2 π \sqrt{\frac{2 R}{3 g}}$
C $2 π \sqrt{\frac{2 R}{g}}$
D $2 π \frac{\sqrt{3 R}}{2} g)$
A disc is made to oscillate about a horizontal axis passing through mid point of its radius. Determine time period.
A $2 π \sqrt{\frac{3 R}{2 g}}$
B $2 π \sqrt{\frac{2 R}{3 g}}$
C $2 π \sqrt{\frac{R}{g}}$
D $2 π \sqrt{\frac{2 R}{g}}$