A uniform rod of length 1.00 m is suspended through an end and is set into oscillation with small amplitude under gravity. Find the time period of oscillation.
To find the time period of oscillation of a uniform rod of length 1.00 m suspended from one end, we can follow these steps:
Step 1: Identify the parameters
- Length of the rod (L) = 1.00 m
- The rod is uniform, so its center of mass is at a distance of L/2 from the pivot point.
Step 2: Determine the distance to the center of mass
- The distance (D) from the pivot point to the center of mass is:
D=L2=1.00m2=0.50m
Step 3: Moment of inertia of the rod about the pivot point
- The moment of inertia (I) of a uniform rod about one end is given by:
I=13mL2
where m is the mass of the rod.
Step 4: Write the formula for the time period (T)
- The formula for the time period of a physical pendulum is:
T=2π√ImgD
Step 5: Substitute the values into the formula
- Substituting I and D into the time period formula:
T=2π
⎷13mL2mgD
- Here, g is the acceleration due to gravity (approximately 9.81m/s2).
Step 6: Simplify the equation
- The mass m cancels out:
T=2π
⎷13L2gD
- Now substitute D=L2:
T=2π
⎷13L2g⋅L2
- This simplifies to:
T=2π√2L3g
Step 7: Substitute L=1.00m and g=9.81m/s2
- Substitute the values:
T=2π√2⋅1.003⋅9.81
- Calculate the denominator:
3⋅9.81=29.43
- Now calculate:
T=2π√229.43≈2π√0.0679
- Calculate the square root:
√0.0679≈0.260
- Finally, calculate T:
T≈2π⋅0.260≈1.63s
Final Answer
The time period of oscillation of the rod is approximately 1.63 seconds.
---
- Length of the rod (L) = 1.00 m
- The rod is uniform, so its center of mass is at a distance of L/2 from the pivot point.
- The distance (D) from the pivot point to the center of mass is:
D=L2=1.00m2=0.50m
- The moment of inertia (I) of a uniform rod about one end is given by:
I=13mL2
where m is the mass of the rod.
- The formula for the time period of a physical pendulum is:
T=2π√ImgD
- Substituting I and D into the time period formula:
T=2π
⎷13mL2mgD
- Here, g is the acceleration due to gravity (approximately 9.81m/s2).
- The mass m cancels out:
T=2π
⎷13L2gD
- Now substitute D=L2:
T=2π
⎷13L2g⋅L2
- This simplifies to:
T=2π√2L3g
- Substitute the values:
T=2π√2⋅1.003⋅9.81
- Calculate the denominator:
3⋅9.81=29.43
- Now calculate:
T=2π√229.43≈2π√0.0679
- Calculate the square root:
√0.0679≈0.260
- Finally, calculate T:
T≈2π⋅0.260≈1.63s
The time period of oscillation of the rod is approximately 1.63 seconds.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Worked Out Examples
22 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Short Answer
13 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
Knowledge Check
A uniform rod of length 2.0 m is suspended through an end and is set into oscillation with small amplitude under gravity. The time period of oscillation is approximately
A1.60secB1.80 secC2.0 secD2.40 secA thin rod of length 1 m is suspended from its end and is made to oscillate in a vertical plane. The distance between the point of suspension and centre of oscillation will be :
A12mB34mC1 mD23mAn infinite nonconducting sheet has surface charge density s. There is a small hole in the sheet as shown in the figure. A uniform rod of length l having linear charge density λ is hinged in the hole as shown. If the mass of the rod is m, then the time period of oscillation for small angular displacement is
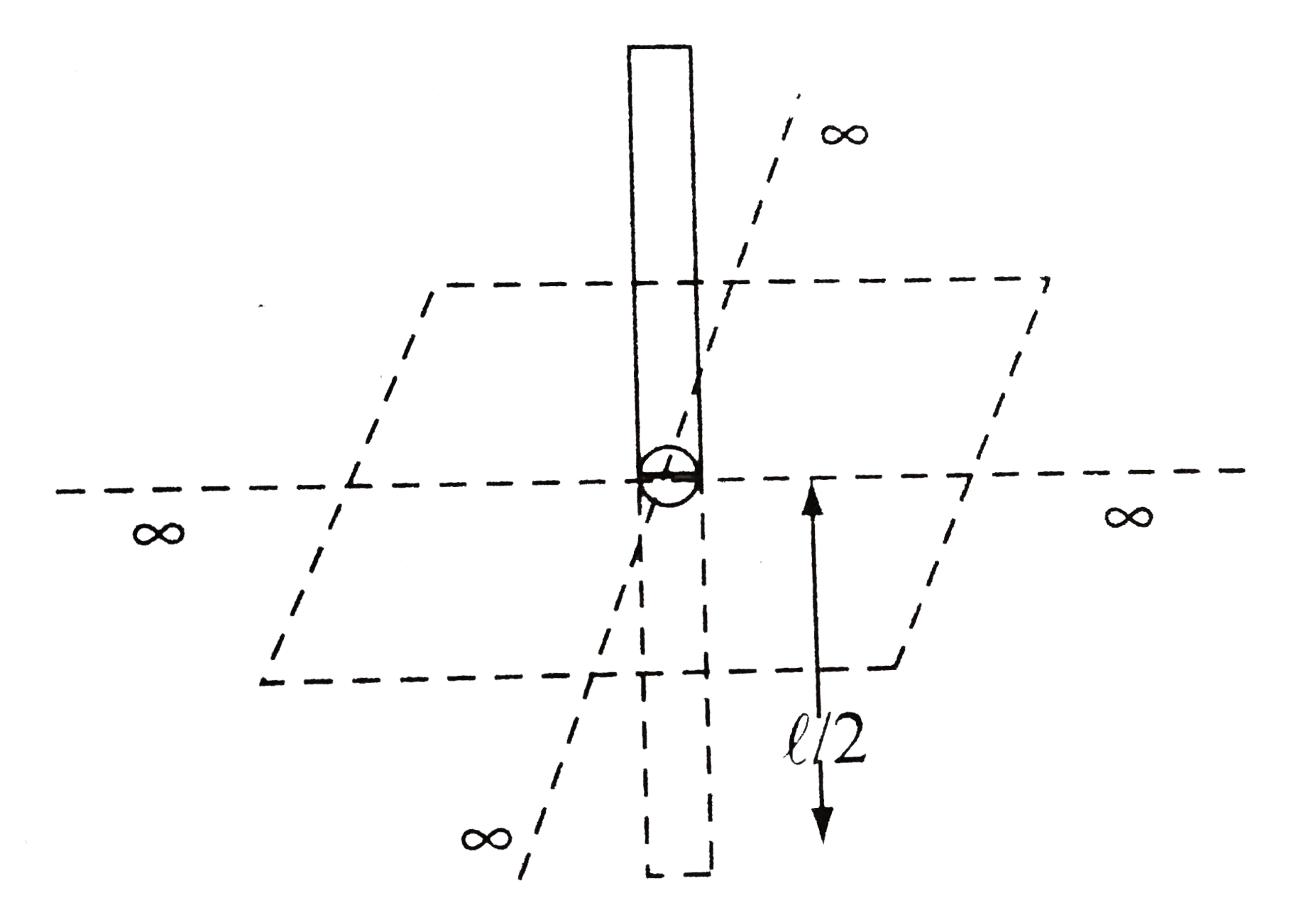 Aπ√mε03σλB2π√2mε03σλCπ2√mε03σλD4π√mε03σλ
Aπ√mε03σλB2π√2mε03σλCπ2√mε03σλD4π√mε03σλ
A uniform rod of length 2.0 m is suspended through its endpoint about which it performs small angular oscillations in the vertical plane, its time period is nearly
View SolutionA uniform rod of mass m and length l is suspended through a light wire of length l and torsional constant k as shown in figure. Find the time perid iof the system makes a. small oscillations in the vertical plane about the suspension point and b. angular oscillations in the horizontal plane about the centre of the rod.
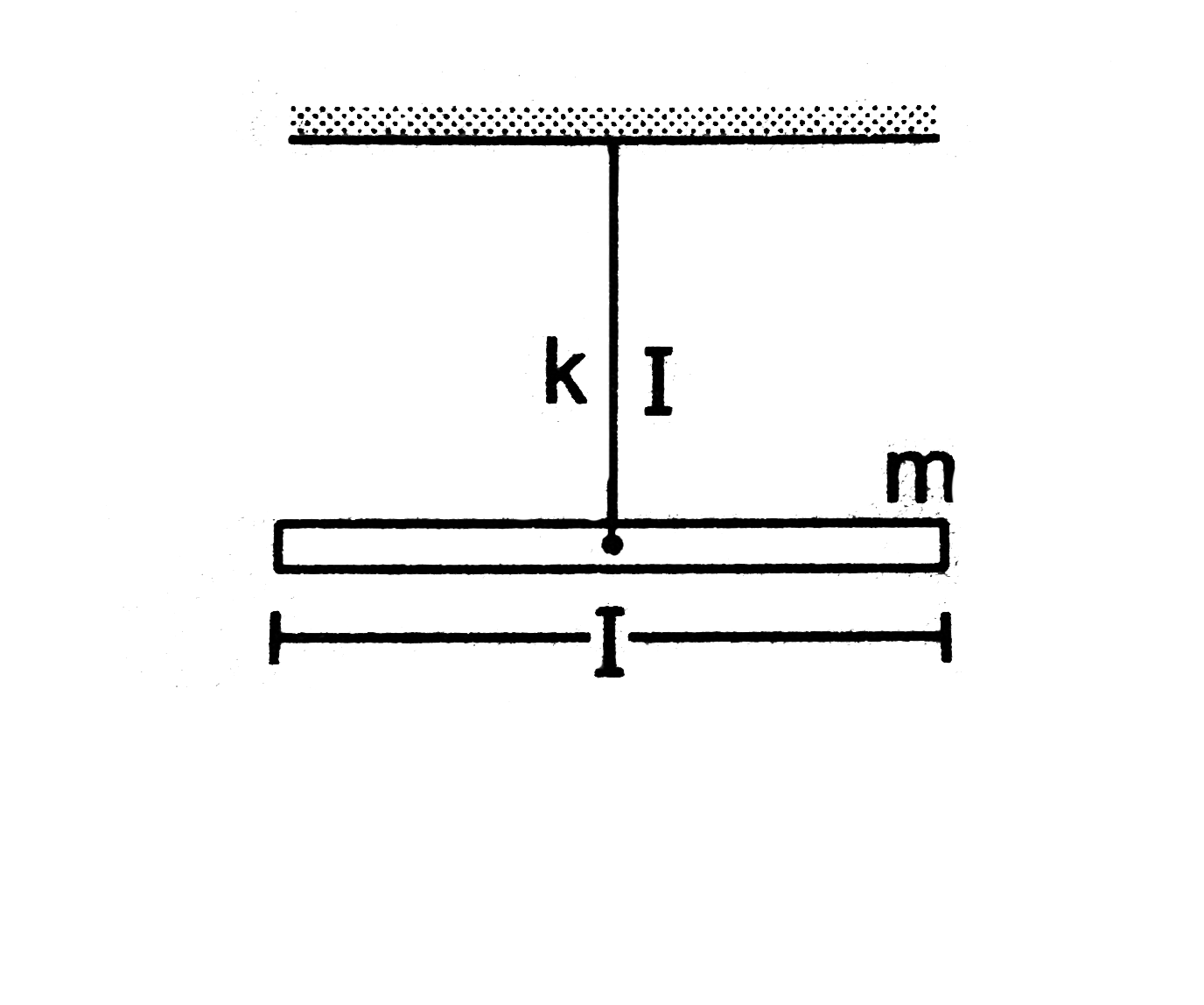
View SolutionA uniform rod of length l is pivoted distance x from the top of the rod . Neglecting friction find the (a) value of x for minimum period of oscillation, (b) minimum period of oscillation of the rod.

View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionA simple pendulum has time period T. A uniform rod, whose length is the same as that of the pendulum, undergoes small oscillations about its upper end. Its time period of oscillation will be -
View Solution

