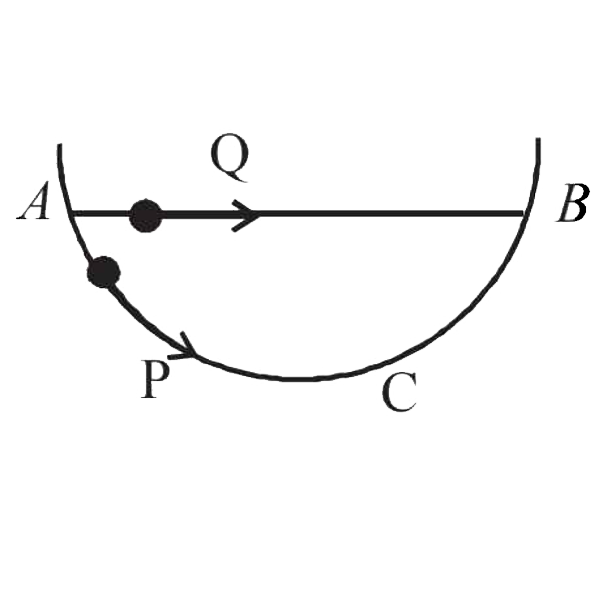
A particle P is sliding down a frictionless hemispherical bowl. It passes the point A at t=0. At this instant of time, the horizontal component of its velocity is v. A bead Q of the same mass as P is ejected from A at t=0 along the horizontal string AB, with the speed v. Friction between the bead and the string may be neglected. Let tP and tQ be the respective times taken by P and Q to reach the point B. Then:
tp<tQ
tp=tQ
tp>tQ
all of these
The correct Answer is:A
Displacement for P and Q is same . The motion of P is accelerated and then retarded. The motion of Q is of constant velocity.
tp<tQ
Topper's Solved these Questions
Similar Questions
A particle is projected with a speed v and an angle θ to the horizontal. After a time t, the magnitude of the instantaneous velocity is equal to the magnitude of the average velocity from 0 to t. Find t.
View SolutionA block of mass m slides 0n a frictionless table. It is constrained to move inside a ring of radius R . At time t=0 , block is moving along the inside of the ring (i.e. in the tangential direction) with velocity v0 . The coefficient of friction between the block and the ring is μ . Find the speed of the block at time t .

View Solution
Knowledge Check
In a projectile motion let vx and vy are the horizontal and vertical components of velocity at any time t and x and y are displacements along horizontal and vertical from the point of projection at any time t.Then
Avy−t graph is a straight line with negative slope and positive interceptBx−tgraph is a straight line passing through originCy−t graph is a straight line passing through originDux−t graph is a straight lineA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
A√TlmB√2TlmC√3TlmD√TmlA particle moves move on the rough horizontal ground with some initial velocity V0. If 34 of its kinetic enegry lost due to friction in time t0. The coefficient of friction between the particle and the ground is.
AV02gt0BV04gt0C3V04gt0DV0gt0
A particle of mass m is projected at t=0 from the point P on the ground with speed v0 at an angle of θ to the horizontal. Find the magnitude and direction of the angular momentum of the particle at time t=v0sinθ2g.
View SolutionIn the shown figure two beads slide along a smooth horizontal rod as shown in figure. The relation between v and v0 in the shown position will be

View SolutionA aprtical moves on a rough horizontal ground with same initial velocity say v0. If (3/4)th of its kinetic energy is lost in friction in time t0 , then coefficient of friction between the partical and the ground is:
View SolutionA particle is projected from a point at an angle with the horizontal at t=0. At an instant t, if p is linear momentum, x is horizontal displacement, y is vertical displacement, and E is kinetic energy of the particle, then which of the following graphs are correct?
View SolutionTwo particles P and Q are moving as shown in the figure. At this moment of time the angular speed of P w.r.t. Q is
View Solution
