A particle is released from the top of the smooth hemisphere R as shown.
the normal contact between the particle and the hemisphere in position θ is

mg(3−2cosθ)
mg(3cosθ−2)
mg(4cosθ−3)
mg(4−3cosθ)
The correct Answer is:B
v2=2gh=2gR(1−cosθ)
mgcosθ−N=mv2R=2mg(1−cosθ)
N=mg(3cosθ−2)
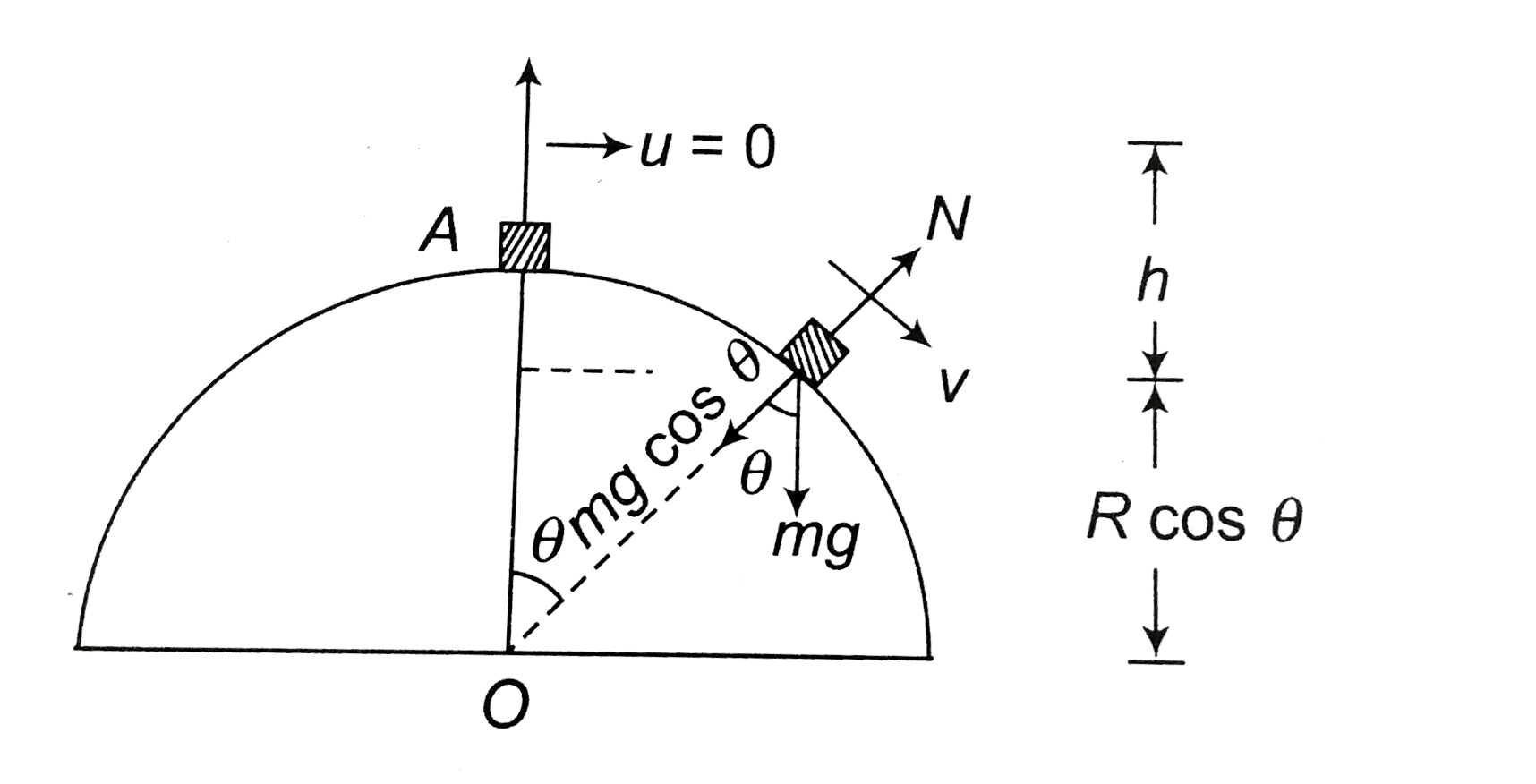
Topper's Solved these Questions
Similar Questions
A particle is released from the top of a smooth hemisphere.find the angle rotated by the radius through the particle, when it loses contract with the hemisphere. Also sketch variation of normal contact force with cosθ, where θ is an angle rotated by the radius through the particle.
View SolutionA particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed μ. Calculate the angle with verticle where it loses contact with the hemisphere.
View Solution
Knowledge Check
- Question 1 - Select One
A particle is placed at rest inside a hollow hemisphere of radius R. The coefficient of friction between the particle and the hemisphere is μ=1√3. The maximum height up to which the particle can remain stationary is
AR2B(1−√32)RC√32RD3R8 - Question 2 - Select One
In the figure shown, a particle is released from the position A on a smooth track. When the particle reaches at B, then normal reaction on it by the track. When the particle reaches at B, then normal reaction on it by the track is
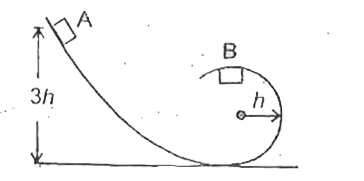 AmgB2mgC23mgDm2gh
AmgB2mgC23mgDm2gh - Question 3 - Select One
A partcle rests on the top of a hemisphere of radius R. Find the smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down :
A√gRB√2gRC√3gRD√5gR
A hemisphere of radius R and of mass 4m is free to Slide with its base on a smooth horizontal table. A particle mass m is placed on the top of the hemisphere. Find the angular velocity of the particle relative to hemisphere at an angular displacement θ when velocity of hemisphere has become v.
 View Solution
View SolutionA particle of mass m is placed in equlibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position θ with the vertical wheere cosθ35. if the work done against frictiion is 2mgR10x, find x.
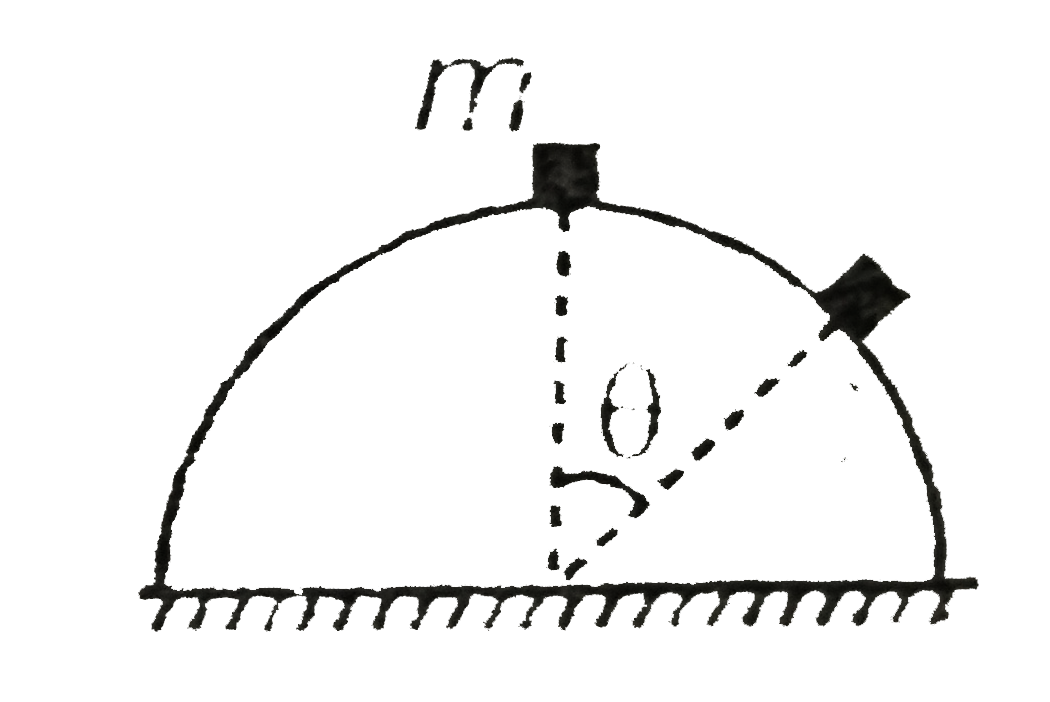 View Solution
View SolutionA smooth sphere of radius R is moving in a straight line with an acceleration a. A particle is released from top of the sphere from rest. Find the speed of the particle when it is at an angular position θ from the initial position relative to the sphere.
View SolutionA hemisphere of radius R and mass 4 m is free to slide with its base on a smooth horizontal table . A particle of mass m is placed on the top of the hemisphere . The angular velocity of the particle relative to centre of hemisphere at an angular displacement θ when velocity of hemisphere has become v is
View SolutionConsider the situation as shown in the figure. A solid sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls along the surface. Find the normal contact force between the solid sphere and the cup at the bottom most point.
 View Solution
View Solution

