A ball reaches a racket at 60m/s along +X dirction and leaves the racket in the opposite direaction with the same speed. Assuming that the mass of the ball as 50gm and the contact time is 0.02 second the force exerted by the racket on the ball is .
300N along +X direction
300N along −X direction
3,00,000N along +X direction
3,00,000N along −X direction
The correct Answer is:B
To solve the problem step by step, we will use the concepts of momentum, force, and acceleration.
Step 1: Identify the given data
- Initial velocity of the ball, u=60m/s (in the +X direction)
- Final velocity of the ball, v=−60m/s (in the opposite direction)
- Mass of the ball, m=50g=0.05kg
- Contact time, t=0.02s
Step 2: Calculate the change in velocity (Δv)
The change in velocity is given by:
Δv=v−u=−60m/s−60m/s=−120m/s
Step 3: Calculate the acceleration (a)
Acceleration is defined as the change in velocity over time:
a=Δvt=−120m/s0.02s=−6000m/s2
Step 4: Calculate the force (F)
Using Newton's second law, the force exerted by the racket on the ball can be calculated using:
F=m⋅a
Substituting the values we have:
F=0.05kg⋅(−6000m/s2)=−300N
Step 5: Conclusion
The force exerted by the racket on the ball is −300N. The negative sign indicates that the force is in the opposite direction to the initial motion of the ball.
---
- Initial velocity of the ball, u=60m/s (in the +X direction)
- Final velocity of the ball, v=−60m/s (in the opposite direction)
- Mass of the ball, m=50g=0.05kg
- Contact time, t=0.02s
The change in velocity is given by:
Δv=v−u=−60m/s−60m/s=−120m/s
Acceleration is defined as the change in velocity over time:
a=Δvt=−120m/s0.02s=−6000m/s2
Using Newton's second law, the force exerted by the racket on the ball can be calculated using:
F=m⋅a
Substituting the values we have:
F=0.05kg⋅(−6000m/s2)=−300N
The force exerted by the racket on the ball is −300N. The negative sign indicates that the force is in the opposite direction to the initial motion of the ball.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - LEVEL -II (C.W)71videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - LEVEL -III31videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - C.U.Q73videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - IV41videos
OSCILLATIONS
Similar Questions
The tennis ball may leave the racket of a top player on the serve with a speed of 65 m/s If mass of the ball is 0.06 kg and is in bontact with the racket for 0.03 sec, what the average force n the ball ?
View SolutionA ball weighing 50g hits a hard surface normally with a speed of 25m/s and rebounds with the same speed. The ball remains in contact with the surface for 0.05s .The average force exerted by the surface on the ball is?
View Solution
Knowledge Check
- Question 1 - Select One
A ball weighing 50g hits a hard surface normally with a speed of 25m/s and rebounds with the same speed. The ball remains in contact with the surface for 0.05s .The average force exerted by the surface on the ball is?
A100 NB10 NC1 ND4 N - Question 2 - Select One
A ball weighing 10g hits a hard surface vertically with a speed of 5m/s and rebounds with the same speed The ball remains in contact with the surface speed The ball remains in contact with the surface for 0.01s The average force exerted by the surface on the ball is .
A100NB10NC1ND0.1N - Question 3 - Select One
A hockey player receives a corner shot at a speed of 15m/s at angle 30∘ with y-axis and then shoots the ball along x-axis with the speed 30m/s. If the mass of the ball is 150g and it remains in contact with the hockey stick for 0.01s, the force exerted on the ball along x-axis is
 A281NB187.5NC562.5ND375N
A281NB187.5NC562.5ND375N
A 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
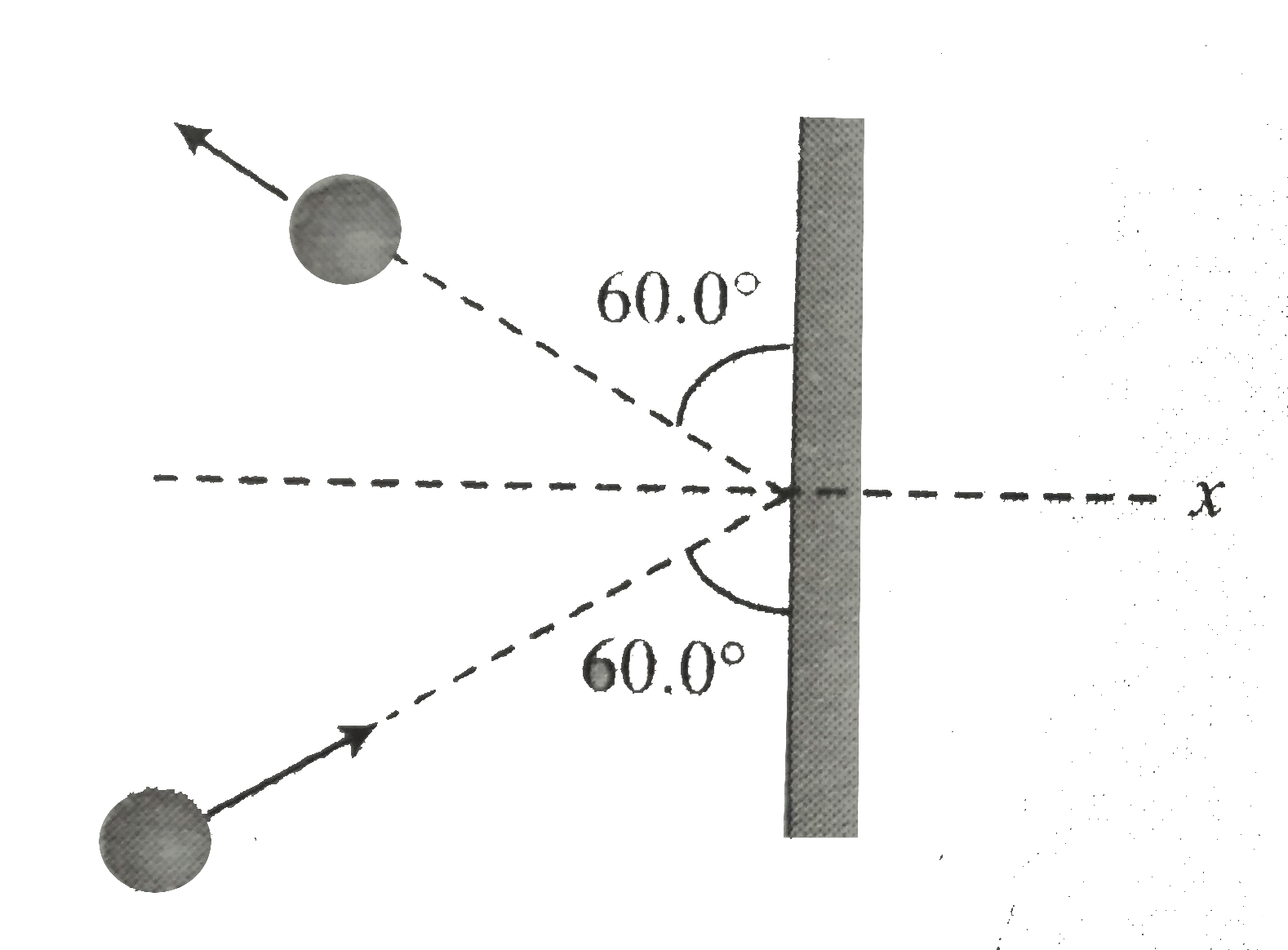 View Solution
View SolutionA 3.00kg steel hall strikes the wall with a speed of 10.0m/s at an angle of 60∘ with the surface. It bounces off with the same speed and angle. If the ball is in contact with the wall for 0.200s, what is the average force exerted by the wall on the ball?
View SolutionA ball weighing 10g hits a hard surface vertically with a speed of 5m/s and rebounds with the same speed The ball remains in contact with the surface speed The ball remains in contact with the surface for 0.01s The average force exerted by the surface on the ball is .
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA bowler tbrows a ball horizontally along east direction with speed of 144km/hr. The batsman hits the ball such that it deviates from its initial direction of motion by 74∘ north of east direction, without changing its speed. If mass of the ball is 13kg and time of contact between bat and ball is 0.02 s. Average force applied by batsman on ball is:
View Solution

