A rectangular box lies on a rough inclined surface The co-efficient of

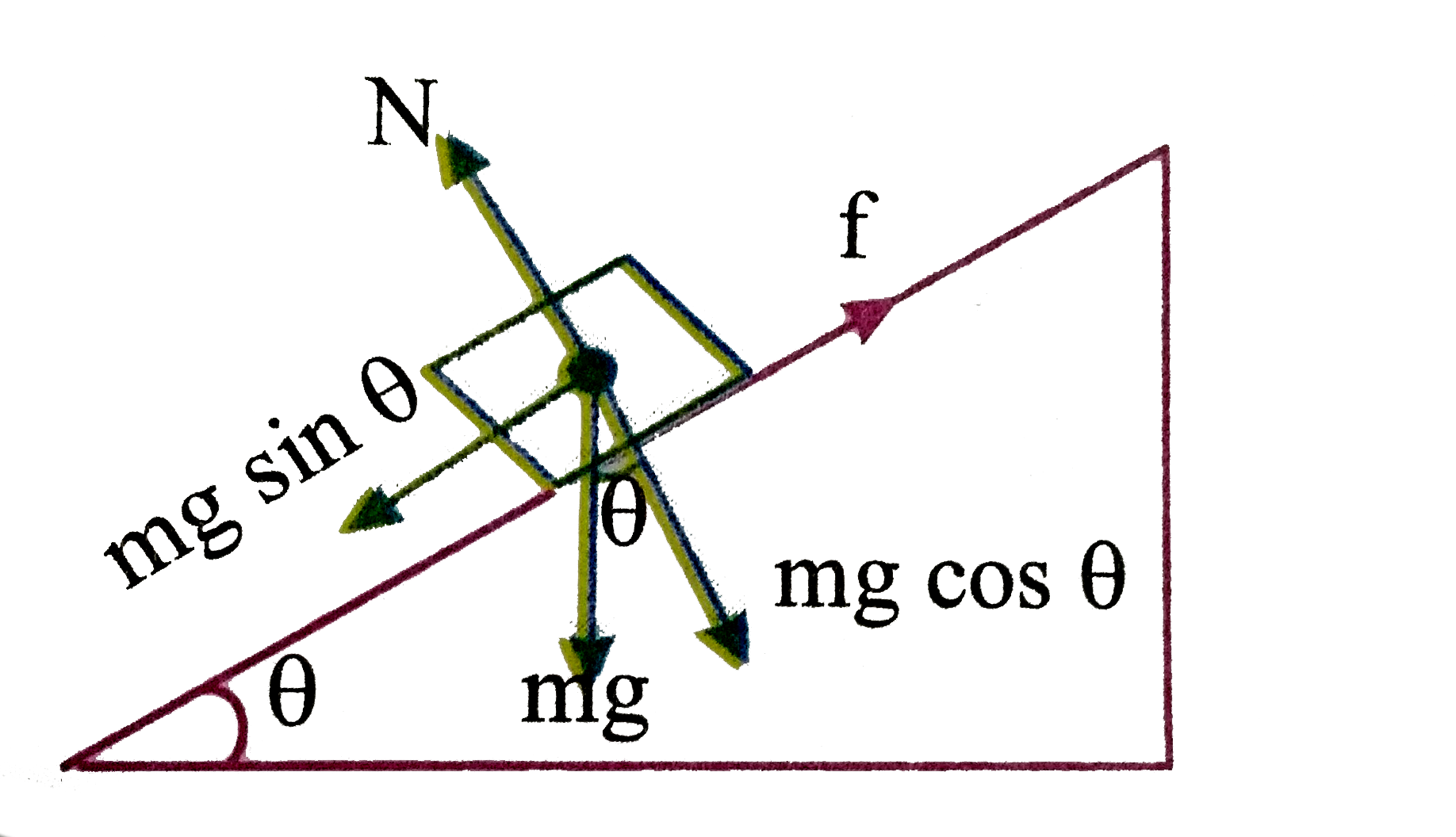Topper's Solved these Questions

BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - SINGLE ANSWER QUESTIONS
35videos
NEWTONS LAWS OF MOTION
BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - SINGLE ANSWER QUESTIONS Passage -1
1videos
NEWTONS LAWS OF MOTION
BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - LEVEL -III
31videos
NEWTONS LAWS OF MOTION
BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W
29videos
MOTION IN A STRAIGHT LINE
BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - IV
41videos
OSCILLATIONS

Knowledge Check

Question 1 - Select One
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is $µ$ . At what angle of inclination $θ$ of the plane to the horizontal will the block just start to slide down the plane?
A $θ = {tan}^{- 1} μ$
B $θ = {cos}^{- 1} μ$
C $θ = {sin}^{- 1} μ$
D $θ = {sec}^{- 1} μ$
Question 2 - Select One
A block of mass m is placed on a rough inclined plane. The corfficient of friction between the block and the plane is $μ$ and the inclination of the plane is $θ$ .Initially $θ = 0$ and the block will remain stationary on the plane. Now the inclination $θ$ is gradually increased . The block presses theinclined plane with a force $m g cos θ$ . So welding strength between the block and inclined is $μ m g cos θ$ , and the pulling forces is $m g sin θ$ . As soon as the pulling force is greater than the welding strength, the welding breaks and the blocks starts sliding, the angle $θ$ for which the block start sliding is called angle of repose $(λ)$ . During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction (frictional force). The net contact force will be resultant of both.
Answer the following questions based on above comprehension:
Q. If $μ = \frac{3}{4}$ then what will be frictional force (shear force) acting between the block and inclined plane when $θ = 30^{\circ}$ :
A $\frac{3 \sqrt{3}}{8} m g$
B $\frac{m g}{2}$
C $\frac{\sqrt{3}}{2} m g$
Dzero
Question 3 - Select One
A block of mass $m$ is placed on a rough inclined plane. The coefficient of friction between the block and the plane is $μ$ and the inclination of the plane is $θ$ . Initially $t h e a t - 0$ and the block will certain stationary on the plane. Now the inclination $θ$ is gradually increased. The block presses the inclined plane with a force $m g cos θ$ . So welding strength between the block and inclined is $μ m g cos θ$ , and the pulling forces is $m g sin θ$ . As soon as the pulling force is greater than the welding strength, the welding breaks and the block starts sliding, the angle $θ$ for which the block starts sliding is called angle of repose $(λ)$ . During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction $($ frictional force $)$ and the shear reaction (frictional force) . The net contact force will be resultant of both.

If the entire system, were accelerated upward with acceleration $' a'$ , the angle of repose , would $:$
Aincreases
Bdecreases
Cremain same
Dincrease of $a > g$

A rectangular box lies on a rough inclined surface The co-efficient of friction beteen the surface and the box is $μ$ . Le the mass of the box ne m What is the force acting on the box down the plane if the angle of inclination of the plane is increased to $α > θ$ ? .

The correct Answer is:C

When angle of incliantion is increased to $α > θ$ then net force acting on the box, down the plane is
$F_{1} = m g sin α f = m g sin α - μ N$
$= m g (sin α - μ cos α)$
.

Topper's Solved these Questions

Similar Questions

Knowledge Check

A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is $µ$ . At what angle of inclination $θ$ of the plane to the horizontal will the block just start to slide down the plane?

NARAYNA-NEWTONS LAWS OF MOTION-NCERT BASED QUESTION

A rectangular box lies on a rough inclined surface The co-efficient of friction beteen the surface and the box is μ. Le the mass of the box ne m What is the force acting on the box down the plane if the angle of inclination of the plane is increased to α>θ ? .

The correct Answer is:C

When angle of incliantion is increased to α>θ then net force acting on the box, down the plane is F1=mgsinαf=mgsinα−μN =mg(sinα−μcosα) .

Topper's Solved these Questions

Similar Questions

Knowledge Check

A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?

NARAYNA-NEWTONS LAWS OF MOTION-NCERT BASED QUESTION

A rectangular box lies on a rough inclined surface The co-efficient of friction beteen the surface and the box is $μ$ . Le the mass of the box ne m What is the force acting on the box down the plane if the angle of inclination of the plane is increased to $α > θ$ ? .

When angle of incliantion is increased to $α > θ$ then net force acting on the box, down the plane is
$F_{1} = m g sin α f = m g sin α - μ N$
$= m g (sin α - μ cos α)$
.

A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is $µ$ . At what angle of inclination $θ$ of the plane to the horizontal will the block just start to slide down the plane?