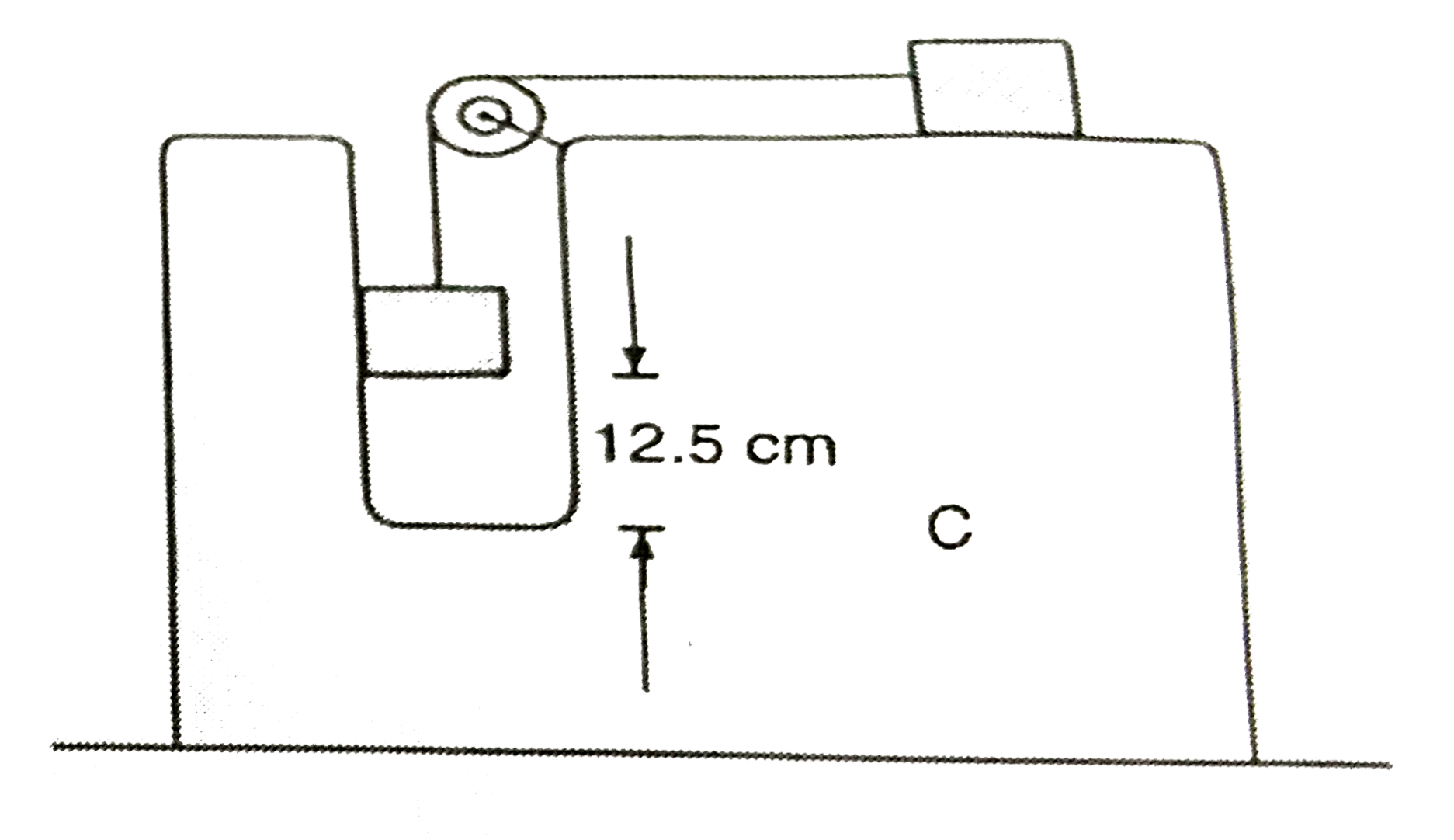
A small, light pulley is attached with a block C of mass 4 kg as shown in fig A block B of mass 1.5kg is placed on the top horizontal surface of C. Another block A of mass 2 kg is hanging from a string, attached with B and passing over the pulley. Taking g=10ms−2 and neglecting friction, acceleration of block C when the system is released from rest is x/4 calculate x.
The correct Answer is:5
Let vertically downward component of acceleration of A be a and let acceleration of C be c (right ward) Then horizontal component of acceleration of A is (right ward) and acceleration of B relative to C is a leftward Hence resultant acceleration of B is (a c) left ward. Now considering free body diagram
For block A,H=2c....(1)2g−T=2a...(2)
For horizontal forces on block B
T=1.5(a−c)...(3) from above equations,
∴ Vertical acceleration of A=a=6.25ms−2 (downward)
Horizontal acceleration of A =c=1.25ms−2 (right ward)
Acceleration of B=(a−c)=5ms−2 (left ward)
Accleration of C=C=1.25ms−2 (right ward)
 .
.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - MULTIPLE ANSWER QUESTIONS9videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - SINGLE ANSWER QUESTIONS Passage -11videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - IV41videos
OSCILLATIONS
Similar Questions
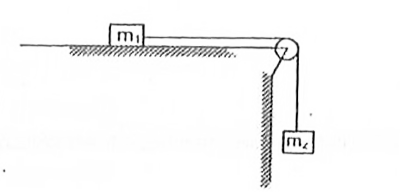
A block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
 View Solution
View SolutionIn the arrangement shown in fig neglect the masses of pulleys and string and also friction Calculate acceleration of blocks A and B
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
Ag, vertically downwardsBg5, vertically downwardsCg25, vertically downwardsDzero - Question 2 - Select One
In the system shown all the surfaces are frictionless while pulley and string are massless. The mass of block A is 2m and that of block B is m. The acceleration of block B immediately after system is released from rest is
 Ag/2BgCg/3DNone of these
Ag/2BgCg/3DNone of these - Question 3 - Select One
Three blocks A,B and C of mass 10 kg each are hanging on a string passing over a fixed frictionless pulley as shown in figure. The tension in the string connecting blocks B and C is (g=10m/s2)
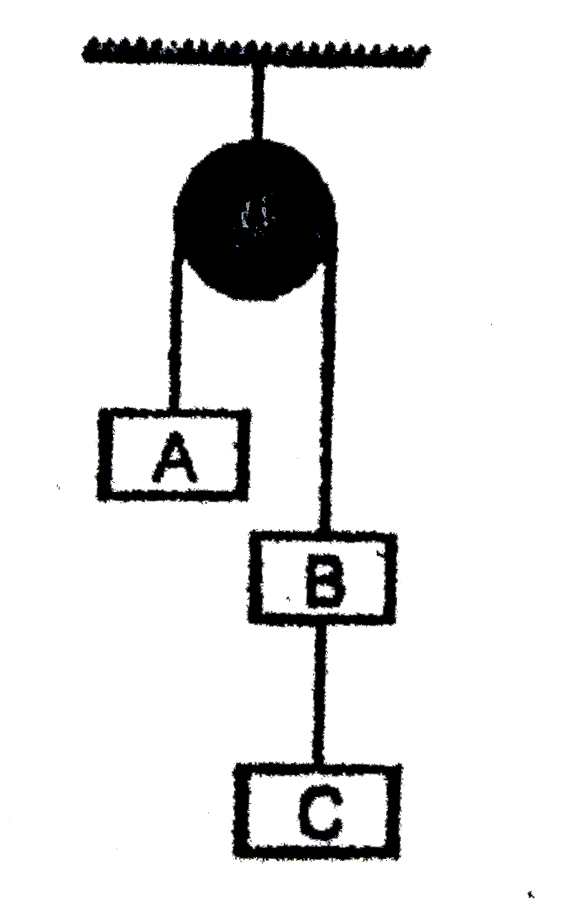 A20003NB4003NC100 ND2003N
A20003NB4003NC100 ND2003N
Two blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.
 View Solution
View SolutionTwo blocks of mass 2 kg and 5 kg are connected by an ideal string passing over a pulley. The block of mass 2 kg is free to slide on a surface inclined at an angle of 30∘ with the horizontal whereas 5 kg block hangs freely. Find the acceleration of the system and the tension in the string.
View SolutionA block A of mass 7 kg is placed on a frictionless table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 3 kg at the other end. The acceleration of the system is (given g=10ms−2)
 View Solution
View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View SolutionA block of mass 2kg is placed on the surface of trolley of mass 20kg which is on a smooth surface.The coefficient of friction between the block and the surface of the trolley is 0.25.If a horizontal force of 2N acts on the block, the acceleration of the system in ms−2 is (g=10ms−2)
View Solution

