A metallic cube of side length 1.5m and of mass 3.2 metric ton is on horizontal rough sloor. The minimum horizontal force that should be applied on the cube at a height 1.2m from that floor to turn the cube about its lower edge is
1.96×103N
4.9×103N
1.96×104N
4.9×104N
The correct Answer is:C
τcw=τAcw,F×1.2=mg×L2,F=1.96×104N
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - NCERT based questions15videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level -I(H.W)58videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-II(C.W.)64videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point that is directly above the centre of the face, at a height 3a/4 above the base. The minimum value of F which the cube begins to tip about the edge is ....(Assume that the cube does not slide).
View SolutionA cubical block of side a and of mass m rests on a rough horizontal surface. A horizontal force F is applied to normal to one of the faces at height h above the base h>a/2. What is the minimum value of F for which the cube begins to tip about an edge?
View Solution
Knowledge Check
- Question 1 - Select One
A roller of mass 300kg and of radius 50cm lying on horizontal floor is resting against a step of height 20cm. The minimum horizontal force to be applied on the roller passing through its centre to turn the roller on to the step is
A980NB1960NC2940ND3920N - Question 2 - Select One
A uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point that is directly above the centre of the face, at a height 3a/4 above the base. The minimum value of F which the cube begins to tip about the edge is ....(Assume that the cube does not slide).
Amg4B2mg3C3mg4Dmg - Question 3 - Select One
A uniform cube of side a and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly above the centre of the face, at a height 3a4 above the base. What is the minimum value of F for which the cube begins to tip about an edge?
AmgBmg3C2mg3D5mg3
A uniform cube of side a & mass m rests on a rough horizontal table as shown. A horizontal force F is applied normal to one of the faces at a point that is directly above the centre of the face, at a height 3a4 above the base. The minimum value of F for which the cube begins to tip about an edge is αmgβ. Find (a (aβ) (assume that cube does not slide).
'(##CEN_KSR_PHY_JEE_C09_E01_028_Q15##)'View SolutionA uniform cube of side 'a' and mass m rests on a rough horizontal table. A horizontal force F is applied normal to one of the faces at a point directly below the centre of the face, at a height a/4 above the base.
a. What is the minimum value of F for which the cube begins to tip about an edge?
b. What is the minimum value of its so that toppling occurs?
c. If μ=μmin find minimum force for topping.
d. Find minimum μs so that Fmin can cause toppling.View SolutionIdentical cubes each of mass 'm' and side T' are on the horizontal surface.Then the minimum amount of work done to arrange them one on the other is
View SolutionA uniform cube of side 'b' and mass M rest on a rough horizontal table. A horizontal force F is applied normal to one of the face at a point, at a height 3b/4 above the base. What should be the coefficient of friction (μ) between cube and table so that is will tip about an edge before it starts slipping ?
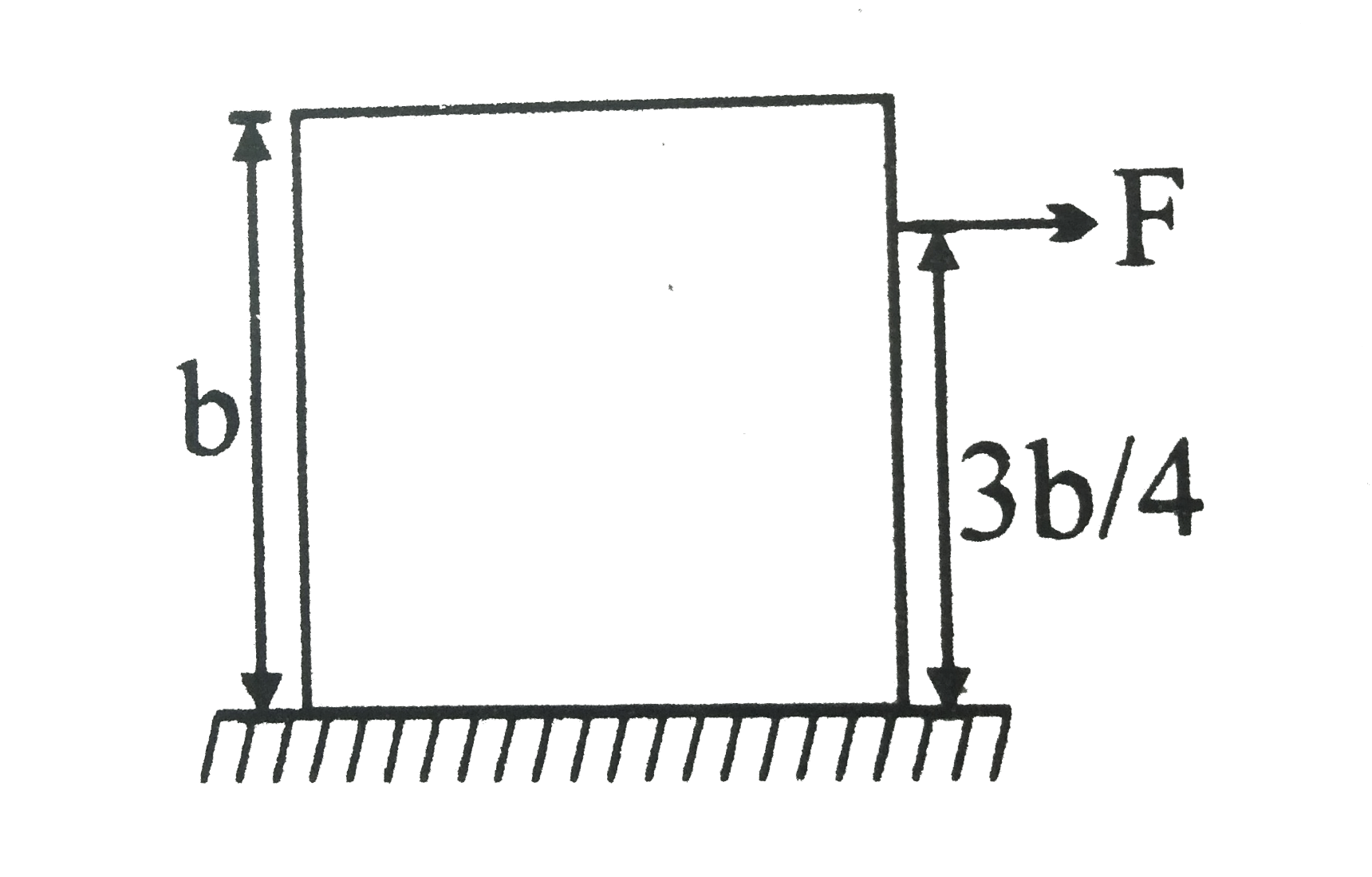 .View Solution
.View SolutionA uniform cube of side and mass m rests on a rough horizontal surface. A horizontal force F is applied normal to one face at point that is directly above the centre of the face at a height a4 above the centre. The minimum value of F for which the cube begins to topple above an edge without sliding is
View Solution

