In the figure shown, a ring A is initially rolling without sliding with a velocity 1, on the horizontal surface of the body B (of same mass as A). All surfaces arc smooth. B has no initial velocity. What will be the maximum height reached by A on B?

3v24g
v24g
v22g
v23g
The correct Answer is:B
When the ring is at the maximum height, the wedge and the ring have the same horizontal component of velocity. As all the surface are smooth, in the absence of friction between the ring and wedge and surface angular velocity of the ring raemains constant.From conservation of mechanical energy
12Mv2+12Iω2=12Mv21+12Iω2+12Mv21+mgh
where v1=final common velocity =v2 h=v24g
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - NCERT based questions15videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level -I(H.W)58videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-II(C.W.)64videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
In the figure shown, a cylinder A is initially rolling with velocity v on the horizontal surface of the wedge B (of same mass as A). All surfaces are smooth and B has no initial velocity. Then maximum height reached by cylinder on the wedge will be.
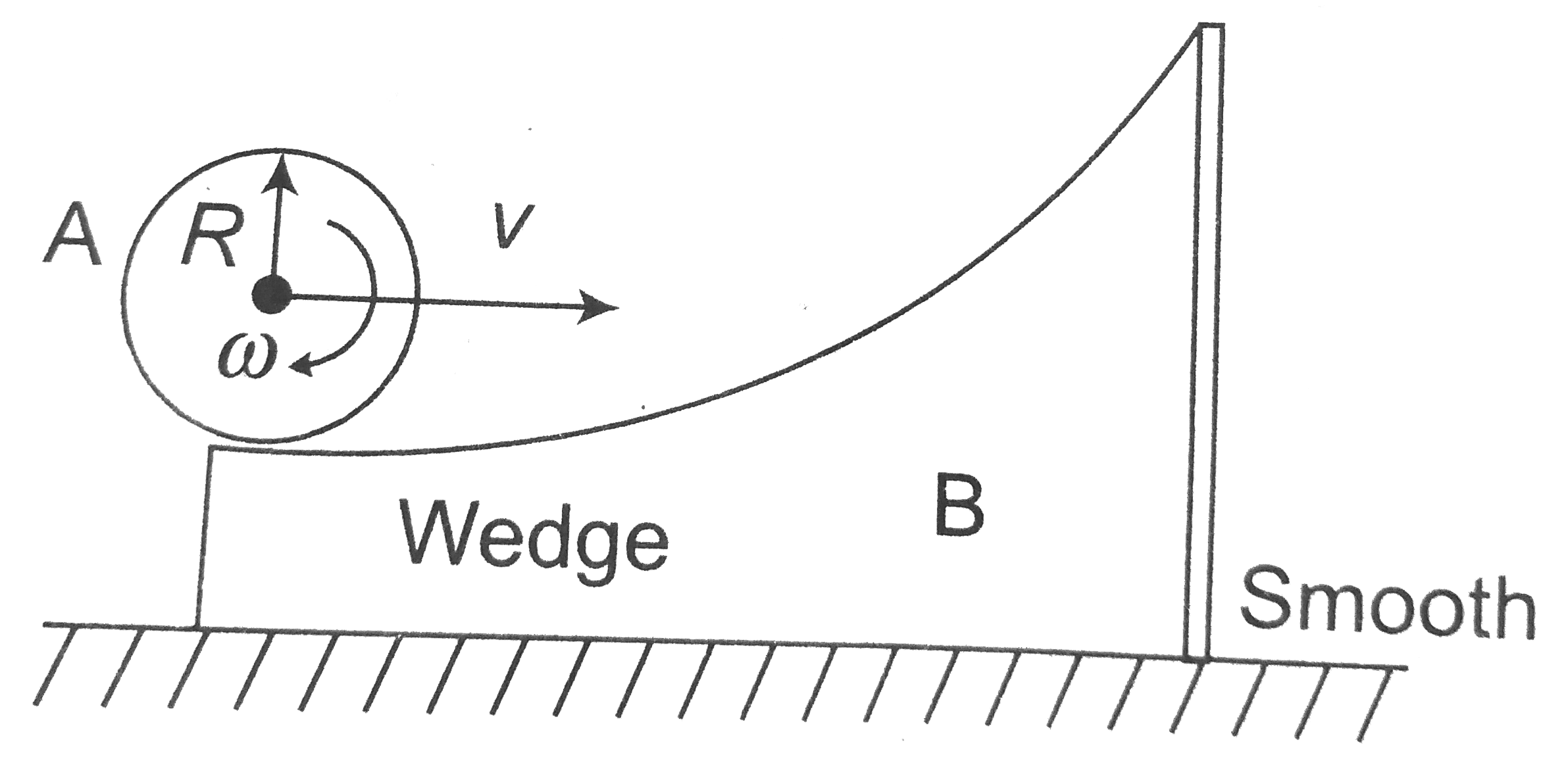 .Av2/4gBv2/gCv2/2gDv2/8
.Av2/4gBv2/gCv2/2gDv2/8 - Question 2 - Select One
As shown in the figure, a disc of mass m is rolling without slipping with angular velocity ω. When it crosses point B disc will be in
 Atranslational motion onlyBpure rolling motionCrotational motion onlyDnone of these
Atranslational motion onlyBpure rolling motionCrotational motion onlyDnone of these - Question 3 - Select One
A uniform disc of mass m and radius r rolls without slipping along a horizontal surface and ramp, as shown above. The disk has an initial velocity of υ . What is the maximum height h to which the center of mass of the disc rises ?
 Ah=υ22gBh=3υ24gCh=υ2gDh=3υ22g
Ah=υ22gBh=3υ24gCh=υ2gDh=3υ22g
For a body thrown vertically up with an initial velocity u ,the maximum height reached by body from the ground is
View SolutionA smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?
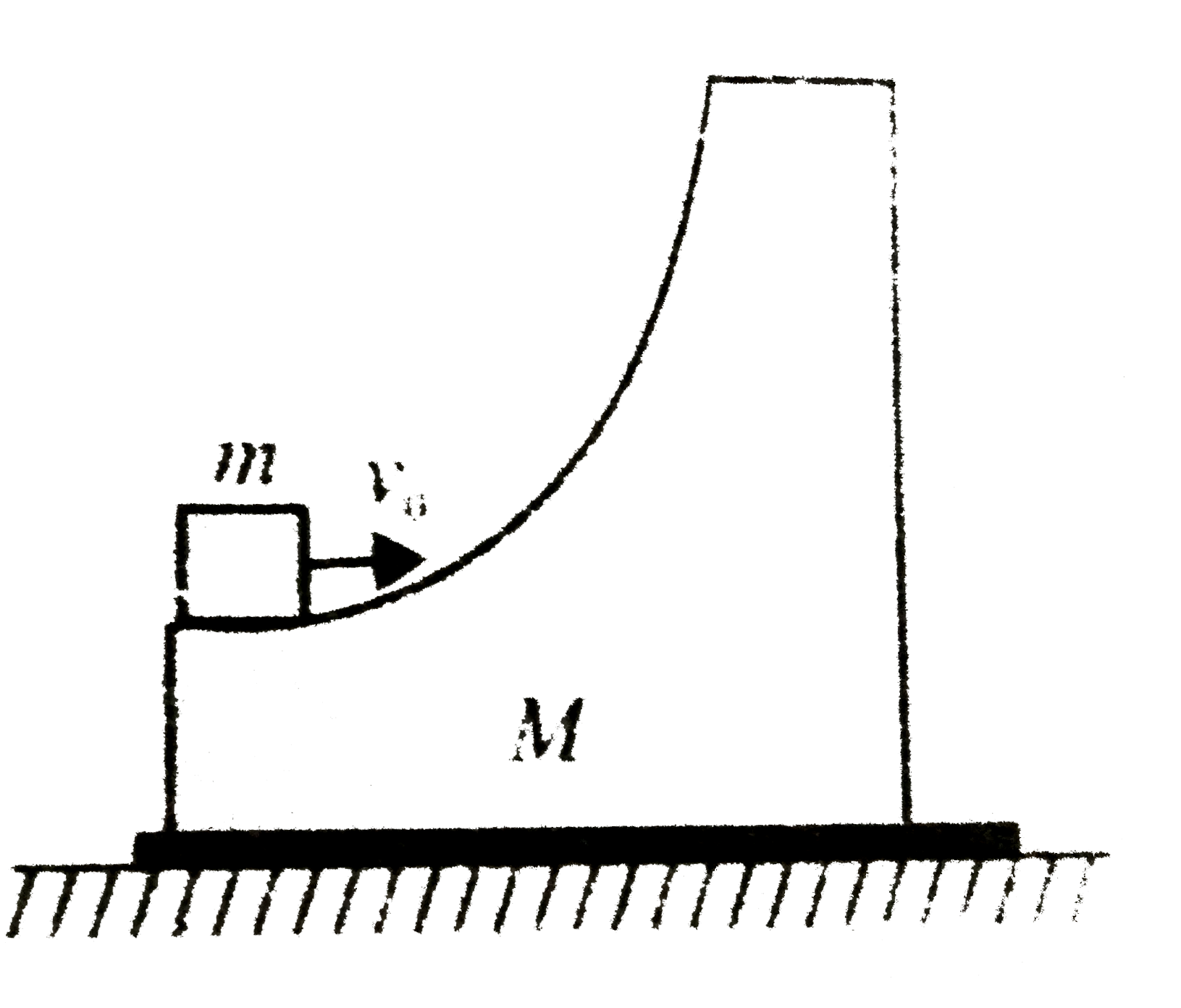 View Solution
View SolutionA body thrown up with a velocity reaches a maximum height of 100 m. Another body with double the mass thrown up with double the initial velocity will reach a maximum height of-
View SolutionA body, thrown upward with some velocity reaches the maximum height of 50m. Another body with double the mass thrown up with double the initial velocity will reach a maximum height of
View SolutionA body, thrown upward with some velocity reaches the maximum height of 50m. Another body with double the mass thrown up with double the initial velocity will reach a maximum height of
View Solution

