The mass of a circular ring is M and its radius is R. Its moment of inertia about an axis in the plane of ring at perpendicular distance R/2 from centre of ring is
MR24
MR22
3MR22
3MR24
The correct Answer is:D
To find the moment of inertia of a circular ring about an axis in its plane at a perpendicular distance of R2 from the center, we can use the parallel axis theorem. Here’s the step-by-step solution:
Step 1: Understand the Moment of Inertia of a Ring
The moment of inertia I of a circular ring about an axis passing through its center and perpendicular to its plane is given by:
Icm=MR2
where M is the mass of the ring and R is its radius.
Step 2: Use the Parallel Axis Theorem
The parallel axis theorem states that if you know the moment of inertia about an axis through the center of mass, you can find the moment of inertia about any parallel axis by adding the product of the mass and the square of the distance between the two axes:
I=Icm+Md2
where d is the distance between the two axes.
Step 3: Identify the Values
In this case:
- Icm=MR2 (moment of inertia about the center)
- d=R2 (the distance from the center to the new axis)
Step 4: Calculate Md2
Now, we need to calculate Md2:
Md2=M(R2)2=MR24
Step 5: Substitute into the Parallel Axis Theorem
Now substitute Icm and Md2 into the parallel axis theorem:
I=MR2+MR24
Step 6: Simplify the Expression
Combine the terms:
I=MR2+MR24=MR2(1+14)=MR2(44+14)=MR2(54)
Final Answer
Thus, the moment of inertia of the circular ring about the specified axis is:
I=54MR2
---
The moment of inertia I of a circular ring about an axis passing through its center and perpendicular to its plane is given by:
Icm=MR2
where M is the mass of the ring and R is its radius.
The parallel axis theorem states that if you know the moment of inertia about an axis through the center of mass, you can find the moment of inertia about any parallel axis by adding the product of the mass and the square of the distance between the two axes:
I=Icm+Md2
where d is the distance between the two axes.
In this case:
- Icm=MR2 (moment of inertia about the center)
- d=R2 (the distance from the center to the new axis)
Now, we need to calculate Md2:
Md2=M(R2)2=MR24
Now substitute Icm and Md2 into the parallel axis theorem:
I=MR2+MR24
Combine the terms:
I=MR2+MR24=MR2(1+14)=MR2(44+14)=MR2(54)
Thus, the moment of inertia of the circular ring about the specified axis is:
I=54MR2
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-V72videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI78videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level -I(H.W)58videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
The mass of a thin circular plate is M and its radius is R. About an axis in the plane of plate at a perpendicular distance R/2 from centre of plate, its moment of inertia is
View SolutionThe mass of a thin circular plate is M and its radius is R. About an axis in the plane of plate at a perpendicular distance R/2 from centre of plate, its moment of inertia is
View Solution
Knowledge Check
- Question 1 - Select One
M is mass and R is radius of a circular ring. The moment of inertia of same ring about an axis in the plane of ring at a perpendicular distance 2R3 from centre of ring is
A2MR23B4MR29C3MR28D17MR218 - Question 2 - Select One
A thin ring has mass 0.25 kg and radius 0.5 m. Its moment of inertia about an axis passing through its centre and perpendicular to its plane is ………… .
A0.0625kgm2B0.625kgm2C6.25kgm2D62.5kgm2
A circular ring of radius 10cm is made of a wire of mass 0.02g/cm. Calculate its radius of gyration and moment of inertia about an axis passing perpendicular to its plane through the centre of the ring.
View SolutionThe mass of a uniform circular ring of radius 0.2m is 0.1kg. Calcuate the moment of inertia of the ring about an axis passing through its centre an perpendicular to its surface.
View SolutionFind moment of inertia of a uniform ring (mass m, radius r) about chord AA' at distance R/2 from center.
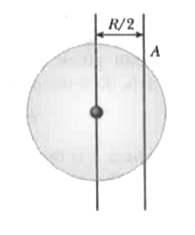 View Solution
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionThe moment of inertia of a uniform circular ring, having a mass M and a radius R, about an axis tangential to the ring and perpendicular to its plane, is
View SolutionFind the out the moment of inertia of a ring having uniform mass distribution of mass M and radius R about an axis which is tangent ot the ring and a in the plane of the ring b. perpendicular to the plane of the ring.
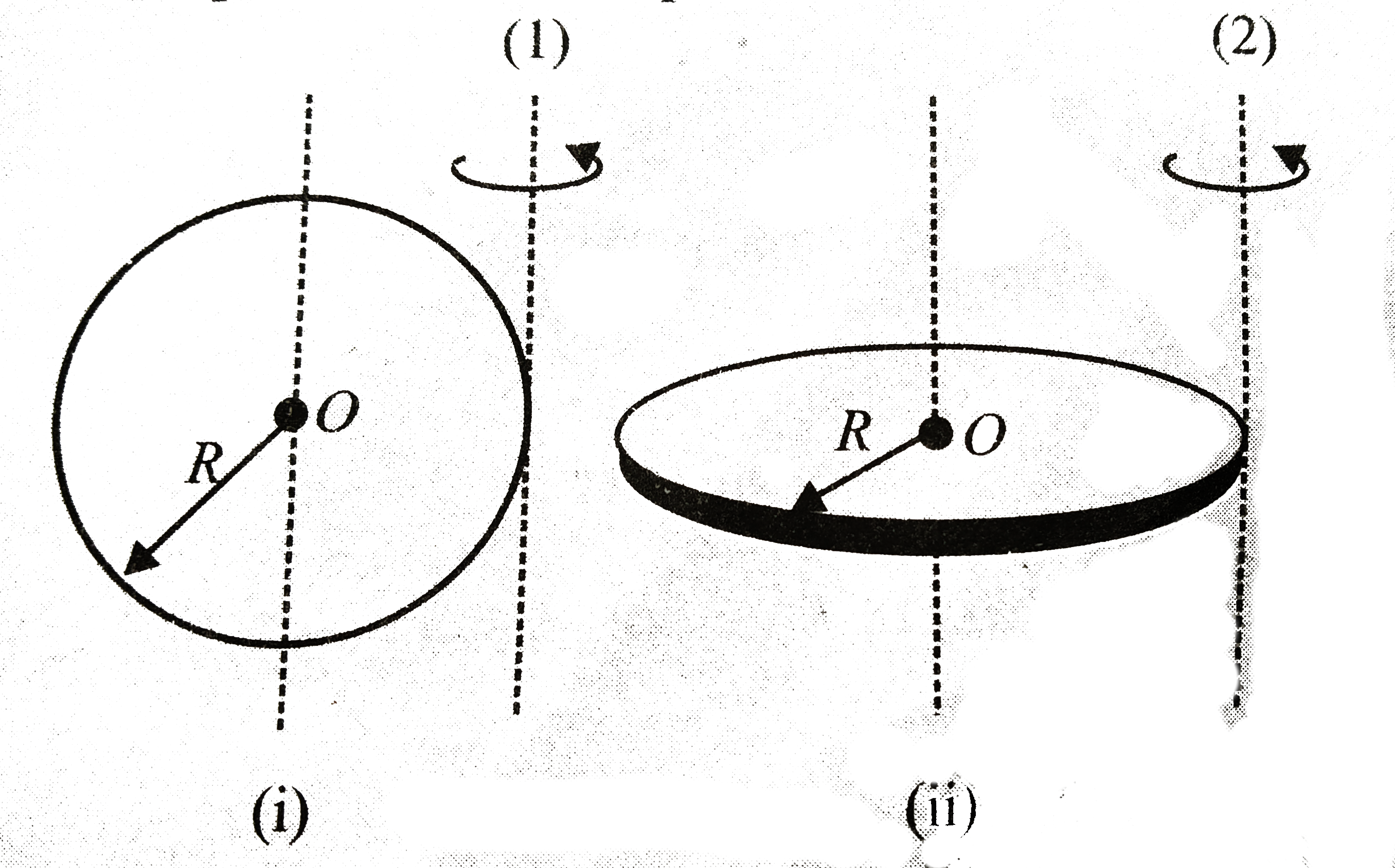 View Solution
View Solution

