A cylinder rolls without slipping on a rough floor, moving with a spped v. It makes an elastic collision with smooth vertical wall. After impact
it will with a speed v initially
its motion will be rolling without slipping
its motion will be rolling without slipping initially and its rotational motion will stop momentarily at some intant
its motion will be rolling without slipping only after some time
The correct Answer is:A, C, D
Let look synopsis given.
v'=ev(←),e=1 so v'=v hence a,c,d are correct
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI78videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level -II(H.W)47videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A solid sphere rolling on a rough horizontal surface with a linear speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. It collides elastically with another identical sphere at rest. There is no friction between the two spheres. Radius of each sphere is R and mass is m.

Linear velocity of first sphere after it again starts rolling without slipping is:View Solution
Knowledge Check
- Question 1 - Select One
A solid sphere rolls without slipping on a rough horizontal floor, moving with a speed v. It makes an elastic collision with a smooth vertical wall. After impact
Ait will move with a speed v initiallBits motion will be rolling with slipping initially and its rotational motion will stop momentarily at some instant.Cits motion will be rolling without slipping only after some timeDall of the above. - Question 2 - Select One or More
A solid sphere rolls without slipping on a rough horizontal floor, moving with a speed v. It makes an elastic collision with a smooth vertical wall. After impact
Ait will move with a speed v initiallyBits motion will be rolling without slippingCits motion will be roilling without slipping initially and its rotational motion will stop momentarily at some instantDits motion will be rolling without slipping only after some time - Question 3 - Select One
Assertion: A ring is rolling without slipping on a rough ground. It strikes elastically with a smooth wall as shown in figure. Ring will stop after some time while travelling in opposite direction.
Reason: After impact net angular momentum about an axis passing through bottommost point and perpendicular to plane of paper is zero.
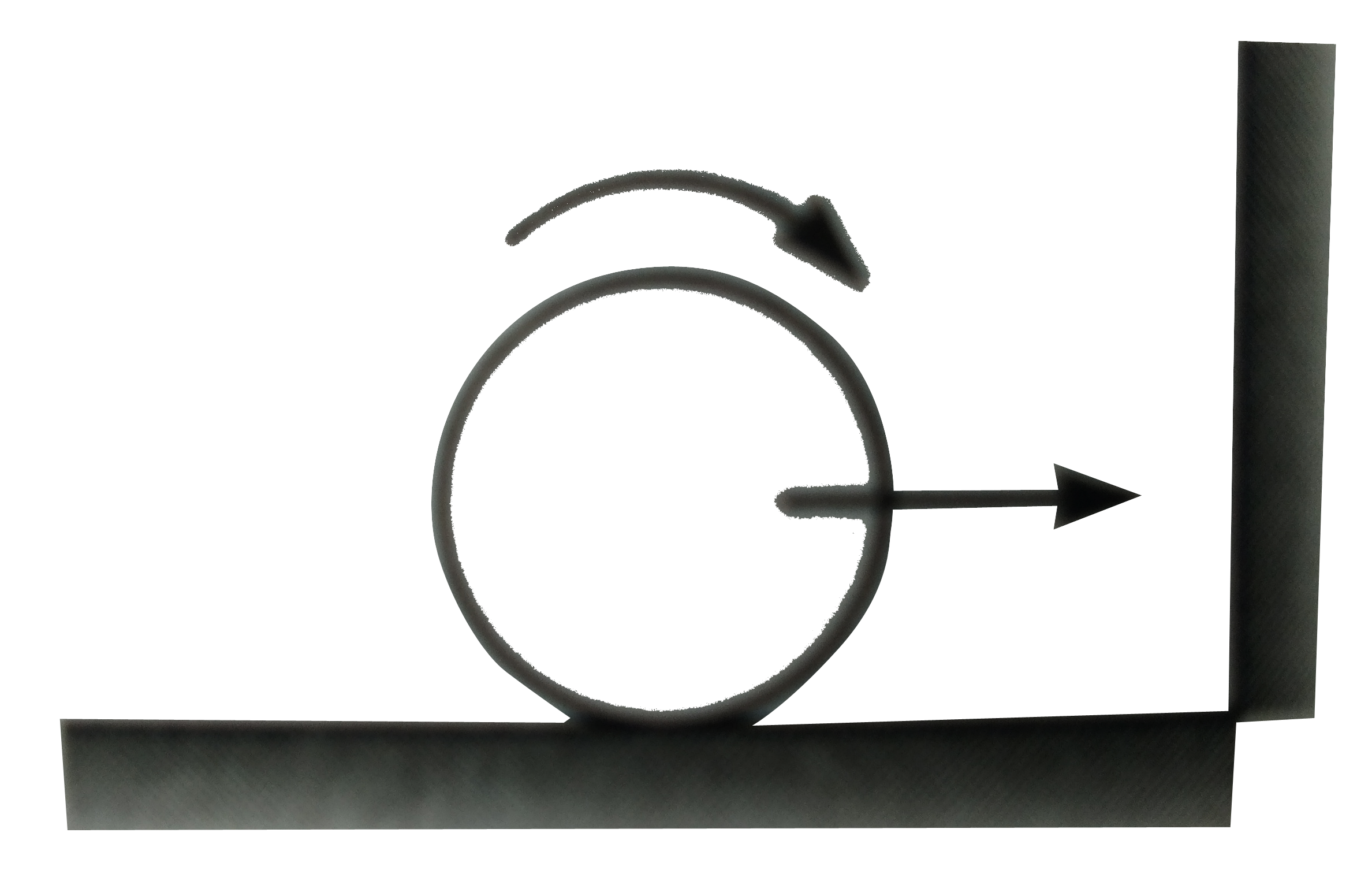 AIf both Assertion and Reason are true and the Reason is correct explanation of the Assertion.BIf both Assertion and Reason are true but Reason is not the correct explanation of Assertion.CIf assertion is true, but the reaction is false.DIf assertion is false but the reason is true.
AIf both Assertion and Reason are true and the Reason is correct explanation of the Assertion.BIf both Assertion and Reason are true but Reason is not the correct explanation of Assertion.CIf assertion is true, but the reaction is false.DIf assertion is false but the reason is true.
A ball rolls without sliding over a rough horizontal floor with velocity v0=7m/s towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is e=0.7. Calculate velocity v of the ball long after the collision.
View SolutionA ball of radius R=20cm has mass m=0.75kg and moment of inertia (about its diameter ) I=0.0125kgm2. The ball rolls without sliding over a rough horizontal floor with velocity v0=10ms−1 towards a smooth vertical wall if coefficient of restitution between the wall and the ball is e=0.7, calculate velocity v of the ball long after the collision. (g=10ms−2)
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
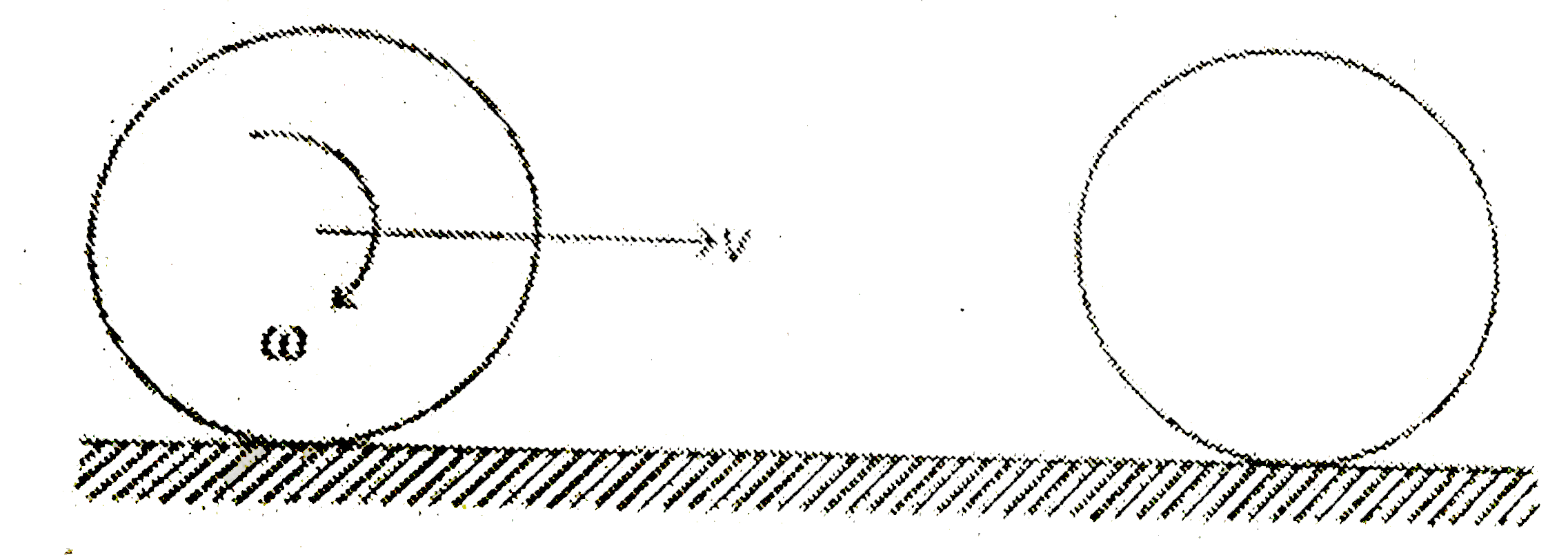
Linear velocity of first sphere after it again starts rolling without slipping isView SolutionA ball is projected from ground with a velocity V at an angle θ to the vertical. On its path it makes an elastic collision with a vertical wall and returns to ground. The total time of flight of the ball is
View SolutionConsider a sphere of mass 'm' radius 'R' doing pure rolling motion on a rough surface having velocity →v0 as shown in the figure. It makes an elastic impact with the smooth wall and moves back and starts rolling after some time again.
 View Solution
View Solution

