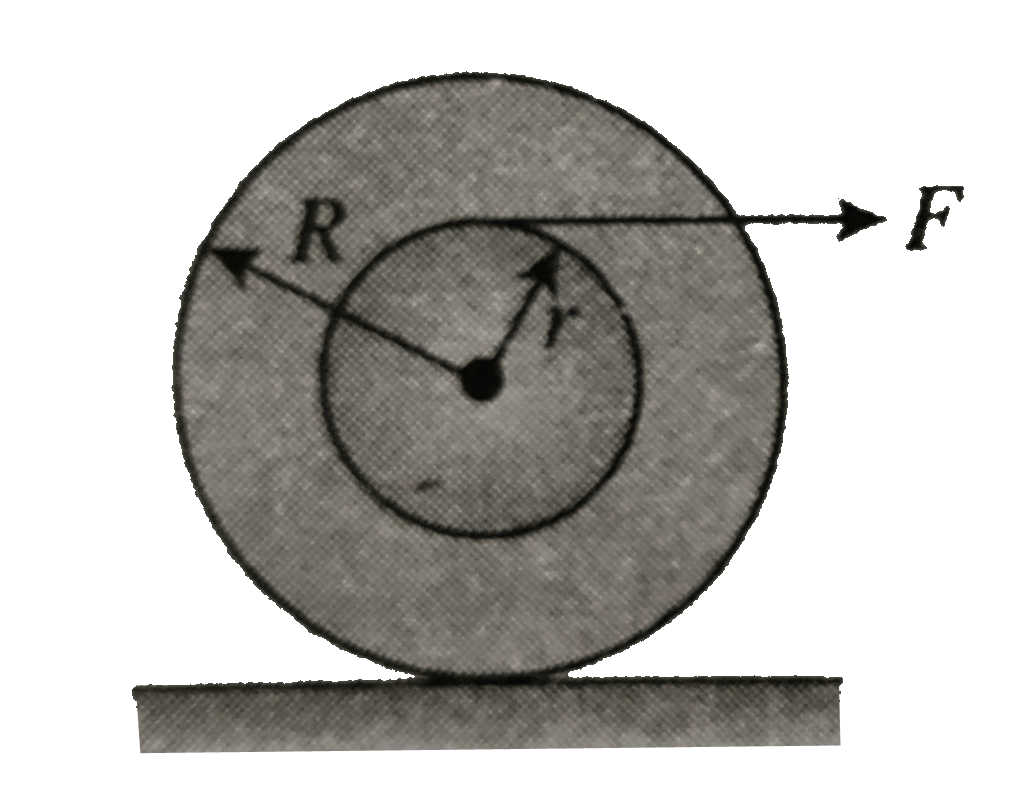
A wheel of radius $R$ , mass $m$ with an axle of radius $r$ is placed on a horizontal surface. Its moment of inertia is $I = m R^{2}$ . Unwinding a rope from its axel a force $F$ is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling $(∠ θ = 0^{\circ})$

Find the condition for which frictional force acts in backward direction

A

$(I / m) > R r$

B

$(2 I / m) > R r$

C

$(\frac{I \sqrt{2}}{m}) > R r$

D

$(\frac{I}{m \sqrt{2}}) > R r$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$F - f m a, F (r) + f (R) = I α$
$a = R α$
Solving $a = \frac{F (r + R) R}{(R + m R^{2})}$ and $f = F - m a$
$= \frac{F [(I / m) - R r]}{[(I / m) + r^{2}]}$
$f$ is positive for $(I / m) > R r$ for frictional force acts in backwards direction.

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A wheel of radius $R$ , mass $m$ with an axle of radius $r$ is placed on a horizontal surface. Its moment of inertia is $I = m R^{2}$ . Unwinding a rope from its axel a force $F$ is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling $(∠ θ = 0^{\circ})$

Find the condition for which frictional force acts in forward direction
A $(I / m) > R r$
B $(2 I / m) > R r$
C $(\frac{I \sqrt{2}}{m}) > R r$
D $(\frac{I}{m \sqrt{2}}) > R r$
Question 2 - Select One
A wheel of radius $R$ , mass $m$ with an axle of radius $r$ is placed on a horizontal surface. Its moment of inertia is $I = m R^{2}$ . Unwinding a rope from its axel a force $F$ is applied to pull it along a horizontal surface. The friction is sufficient enough for its pure rolling $(∠ θ = 0^{\circ})$

Find the linear acceleration of the wheel
A $\frac{F [I / m - R r]}{[(I / m) + r^{2}]}$
B $\frac{2 F [(I / m) - R r]}{[(1 / m) + r^{2}]}$
C $\frac{F [(2 I / m) - \sqrt{2} R r]}{[(I / m) + r^{2}]}$
D $\frac{F [(I \sqrt{2} / m) - R r]}{[(I / m) + r^{2}]}$
Question 3 - Select One
A solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is ?
A $\frac{M R^{2}}{2}$
B $M R^{2}$
C $\frac{3}{2} M R^{2}$
D $2 M R^{2}$

NARAYNA-SYSTEM OF PARTICLES-Level-VI

Home
Ask Doubt
Profile