In the figure shown there is a fixed wedge 'W' of inclination θ. A is a block, B is a disc and 'C' is a solid cylinder. A,B,C each has mass 'm'. Assuming there is no sliding anywhere and string to be of negligible mass find :
The fricition force acting on the cylinder due to the wedge is mg15(1+nsinθ) that n is
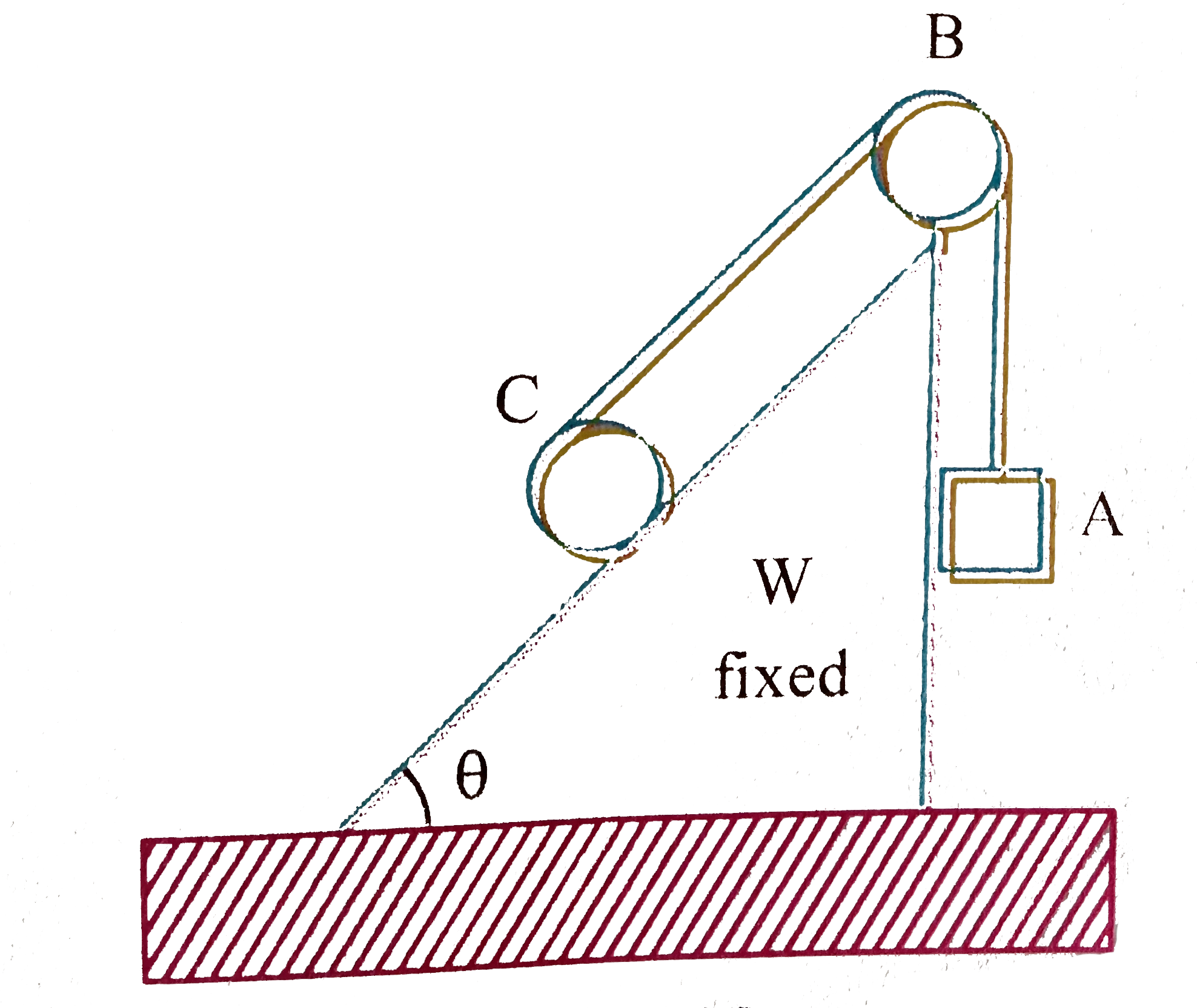
The correct Answer is:7
(a)mg−T1=ma....(1)
⇒T2+f−mgsinθ=ma2.....(2)
(T2−f)r=12mr2×a2r....(3)
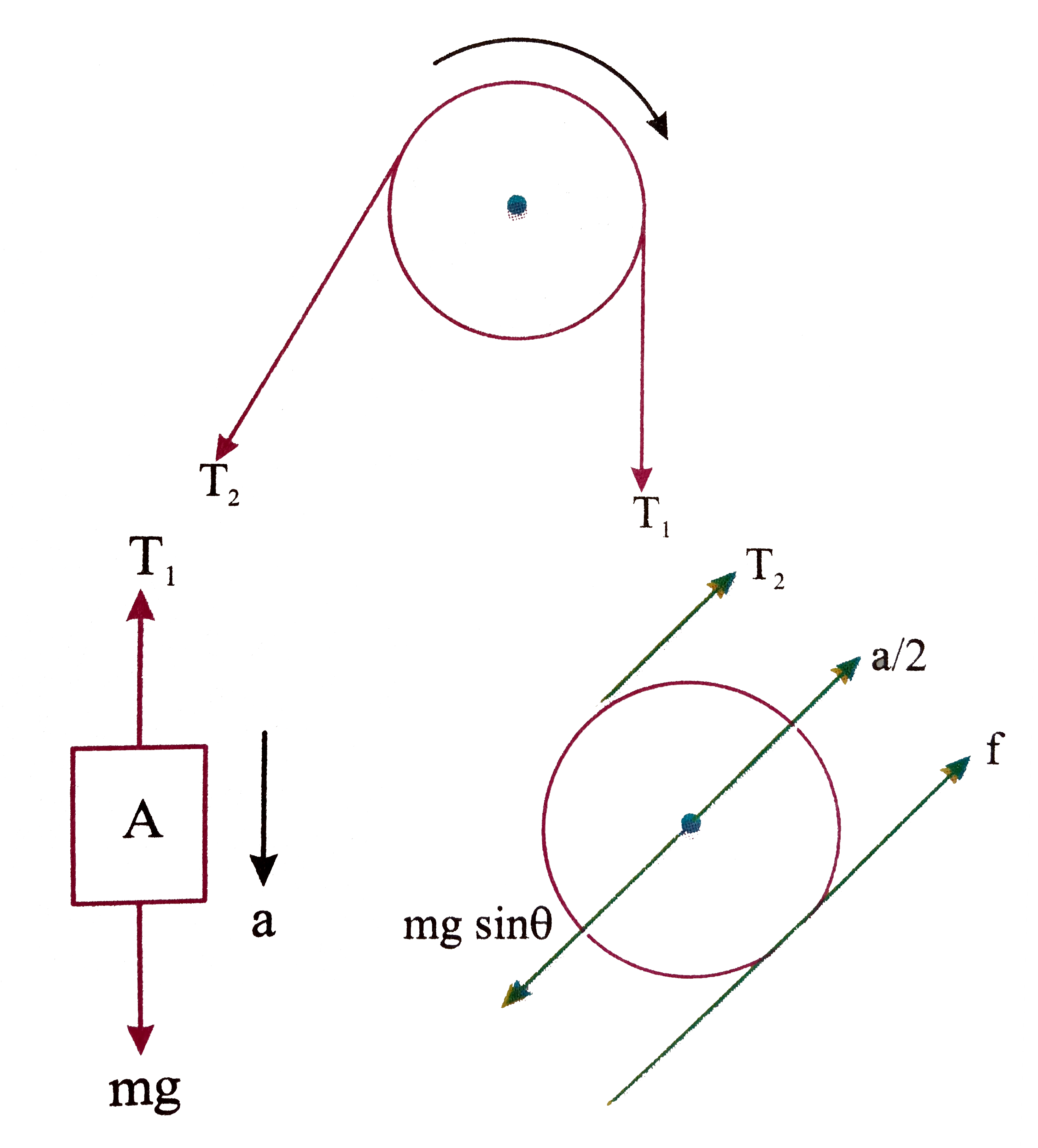
⇒(T1−T2)r=12mr2×ar......(4)
By (1),(2),(3)&(4)
⇒a=4g(2−sinθ)15 substitute this a value we get
f=mg15(1−7)sinθ
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-V72videos
SYSTEM OF PARTICLES
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - IV39videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
A solid cylinder of mass m is wrapped with an inextensible light string and, is placed on a rough inclined plane as shown in the figure. The frictional force acting between the cylinder and the inclined plane is :
 [The coefficient of static friction, μs is 0.4]View Solution
[The coefficient of static friction, μs is 0.4]View SolutionIn the arrangement shown in figure-2.68 the masses of the wedge M and the body m are known. There is no friction at any of the surfaces. The mass of the pulleys and thread is negligible. Find the acceleration of the body m relative to the horizontal surface on which the wedge slides.
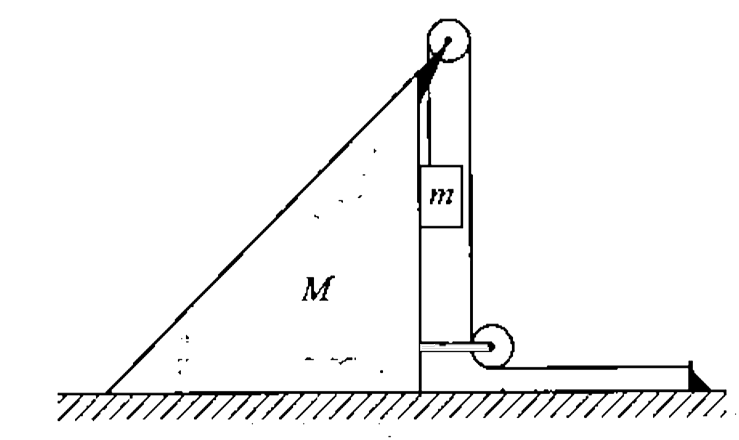
[√2mgM+2m]View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
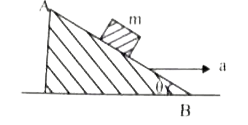 Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθ
Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθ - Question 2 - Select One
A block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.
 Aa=gtanθBa=gcosecθCa=cosθDa=gsinθ
Aa=gtanθBa=gcosecθCa=cosθDa=gsinθ - Question 3 - Select One
Two blocks, each having mass m, are connected with an ideal string through ideal pulleys on a frictionless fixed wedge as shown in the figure. The acceleration of the blocks is
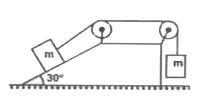 Ag/2Bg/4C2g/3D3g/4
Ag/2Bg/4C2g/3D3g/4
A wedge of mass M lies on a smooth fixed wedge of inclination θ. A particle of mass m lies on the wedge of mass M in the figure. All surfaces are frictionless and the distance of the block from the fixed wedge is l. Find.
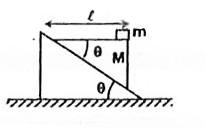
(a) Normal reaction between m and M
(b) the time after which the particle will hit the fixed plane.View SolutionIn the figure shown the pulley is smooth . The spring and the string are light. The block 'B' slides down from the top along the fixed rought wedge of inclination θ. Assuming that the block reaches the end of the wedge. Find the speed of the block at the end. Take the coefficient of friction between the block and the wedge to be μ and the spring was relaxed when the block was relased from the top of the wedge.
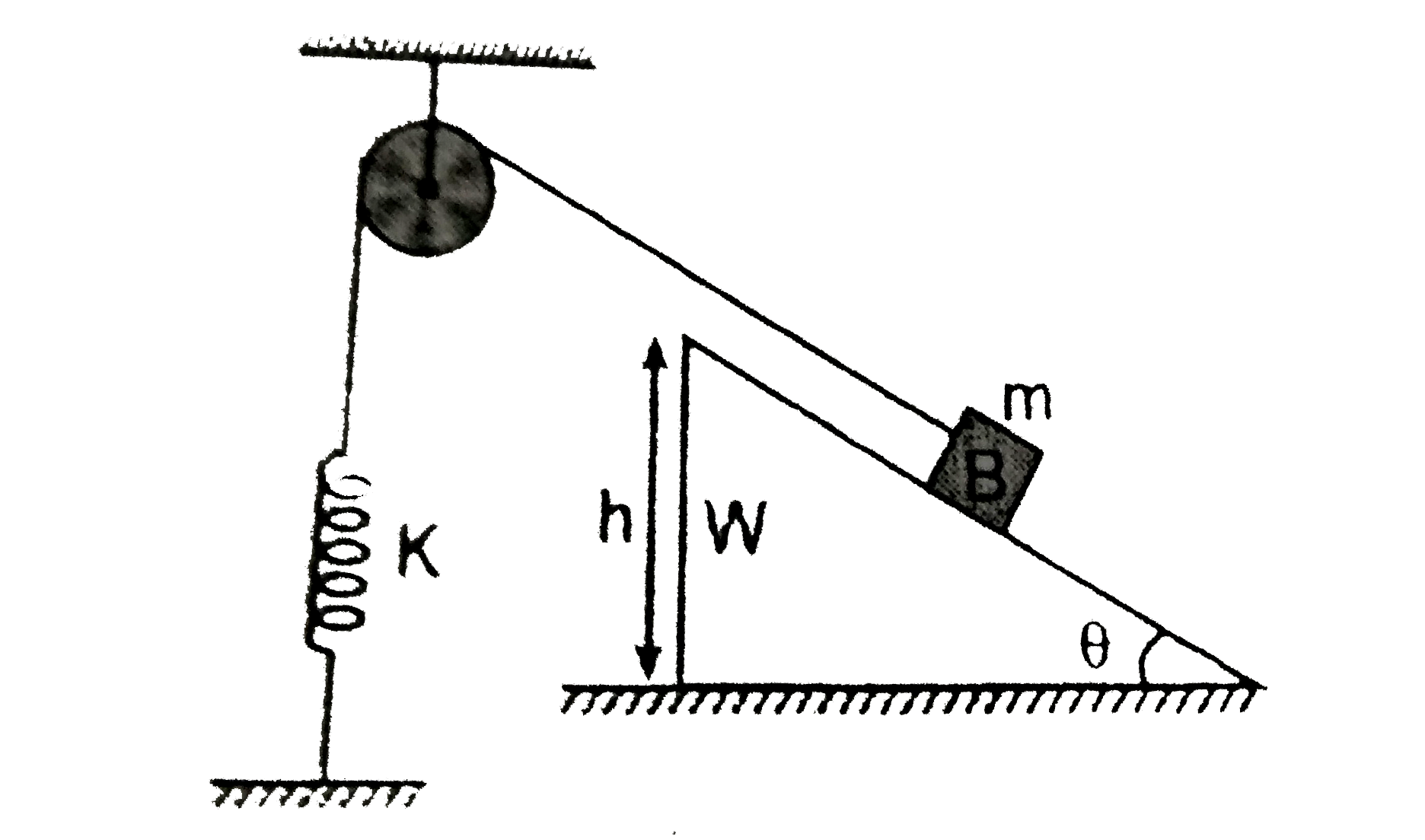 View Solution
View SolutionA horizontal uniform rod of mass 'm' has its left end hinged to the fixed incline plane, while its right end rrests on the top of a uniform cylinder of mass 'm' which in turn is at rest on the fixed inclined plane as shown. The coefficient of friction between the cylinder and rod, and between the cylinder and inclined plane, is sufficient to keep the cylinder at rest.
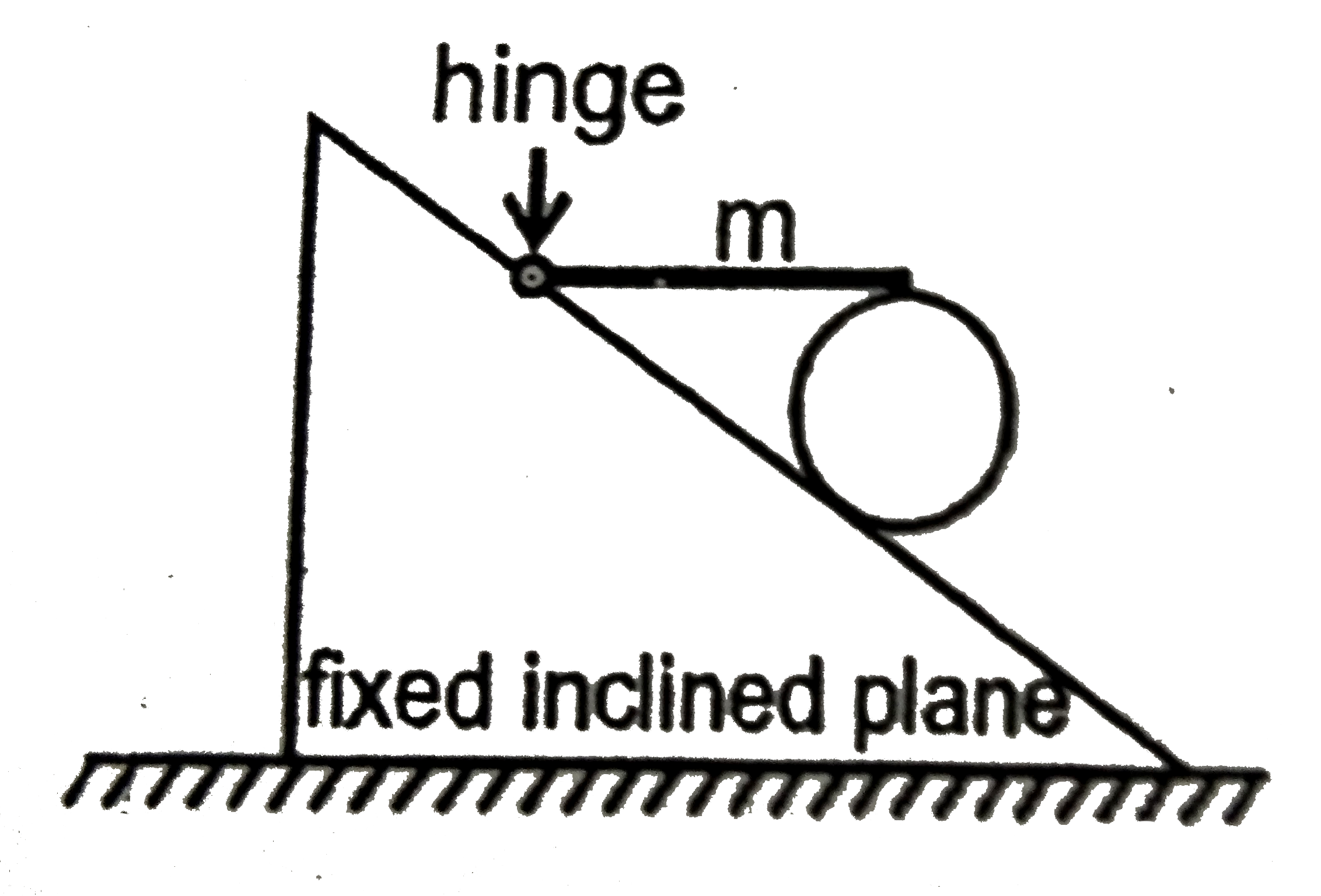
The ratio of magnitude of frictional force on the cylinder due to the rod and the magnitude of frictional force on the cylinder due to the inclined plane is :View SolutionA block of mass m is at rest on wedge as shown in figure. Let N be the normal reaction between two and f the force of friction, then choose the wrong option.
 View Solution
View SolutionAs shown in the figure, a wedge of mass M is placed on a smooth inclined ramp that makes an angle θ to the horizontal. An object of mass m rests on top of the wedge. The sliding down the ramp at acceleration a. determine the apparent weight of the objects as it slides down. noth that there is friction between the object and the wedge so that the object remains relatively at rest on the wedge.
 View Solution
View Solution

