The graph shows the behaviour of a steel wire in the region for whoch the wire obeys Hooke's law. The graph is a parabola. The variables X and Y -axes, respectively can be [ stress (σ),strain (ε) and elastic potential energy(U) ]
![The graph shows the behaviour of a steel wire in the region for whoch the wire obeys Hooke's law. The graph is a parabola. The variables X and Y -axes, respectively can be [ stress (sigma),strain ( epsilon) and elastic potential energy(U) ]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_VO2_C15_EO1_026_Q01.png)
X = stress, Y = strain
X = strain, Y = stress
X = stress, Y = elastic energy
X = elastic energy, Y = stress
The correct Answer is:D
Step by step video, text & image solution for The graph shows the behaviour of a steel wire in the region for whoch the wire obeys Hooke's law. The graph is a parabola. The variables X and Y -axes, respectively can be [ stress (sigma),strain ( epsilon) and elastic potential energy(U) ] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-I (C.W)37videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (C.W)32videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE - III30videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)31videos
MOTION IN A PLANE
Similar Questions
When a uniform metallic wire is stretched the lateral strain produced in it is beta .if sigma and Y are the Poisson's ratio and Young's modulus for wire, then elastic potential energy density of Wire is
View SolutionThe figure shows the y–x graph at an instant for a small amplitude transverse wave travelling on a stretched string. Three elements (1, 2 and 3) on the string have equal original lengths (=Δx). At the given instant-
(i) which element (among 1, 2 and 3) has largest kinetic energy?
(ii) which element has largest energy (i.e., sum of its kinetic and elastic potential energy)
(iii) Prove that energy per unit length ΔEΔx of the string is constant everywhere equal to T(∂y∂x)2 where T is tension the string.
View Solution
Knowledge Check
- Question 1 - Select One
The graph show the behaviour of a length of wire in the region for which the substances obeys Hooke's law. P and Q represent
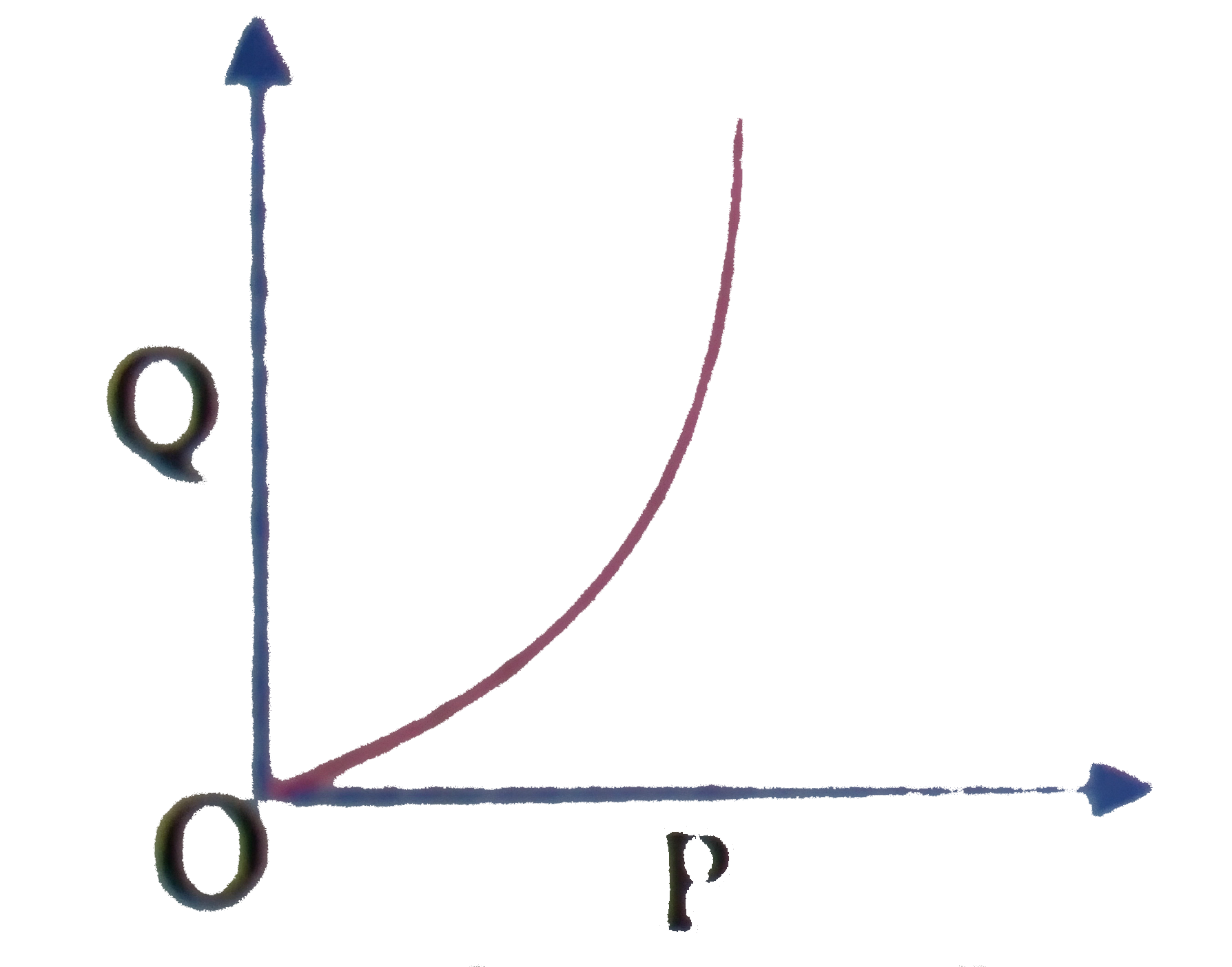AP = applied force, Q = extensionBextension, applied forceCextension, stored elastic energyDstored elastic energy, extension - Question 2 - Select One
The graph shows the behaviout of a length of wire in the region for which the substance obeys Hook's law. D and Q represent
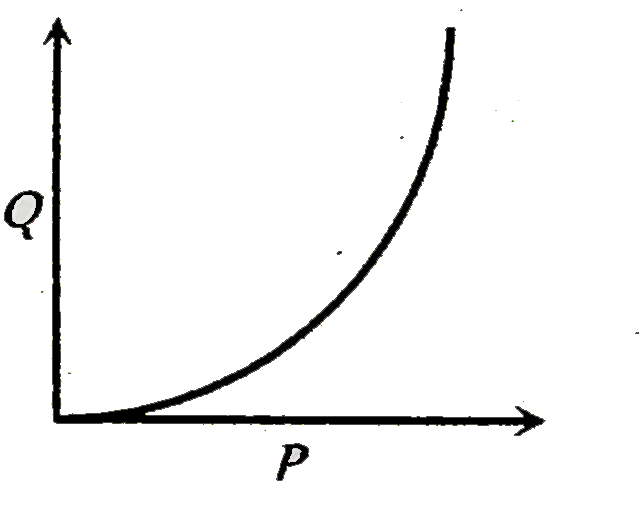AP = applied force, Q = extensionBP = extension, Q = applied forceCP = extension, Q= stored elastic energyDP = stored elastic energy, Q = extension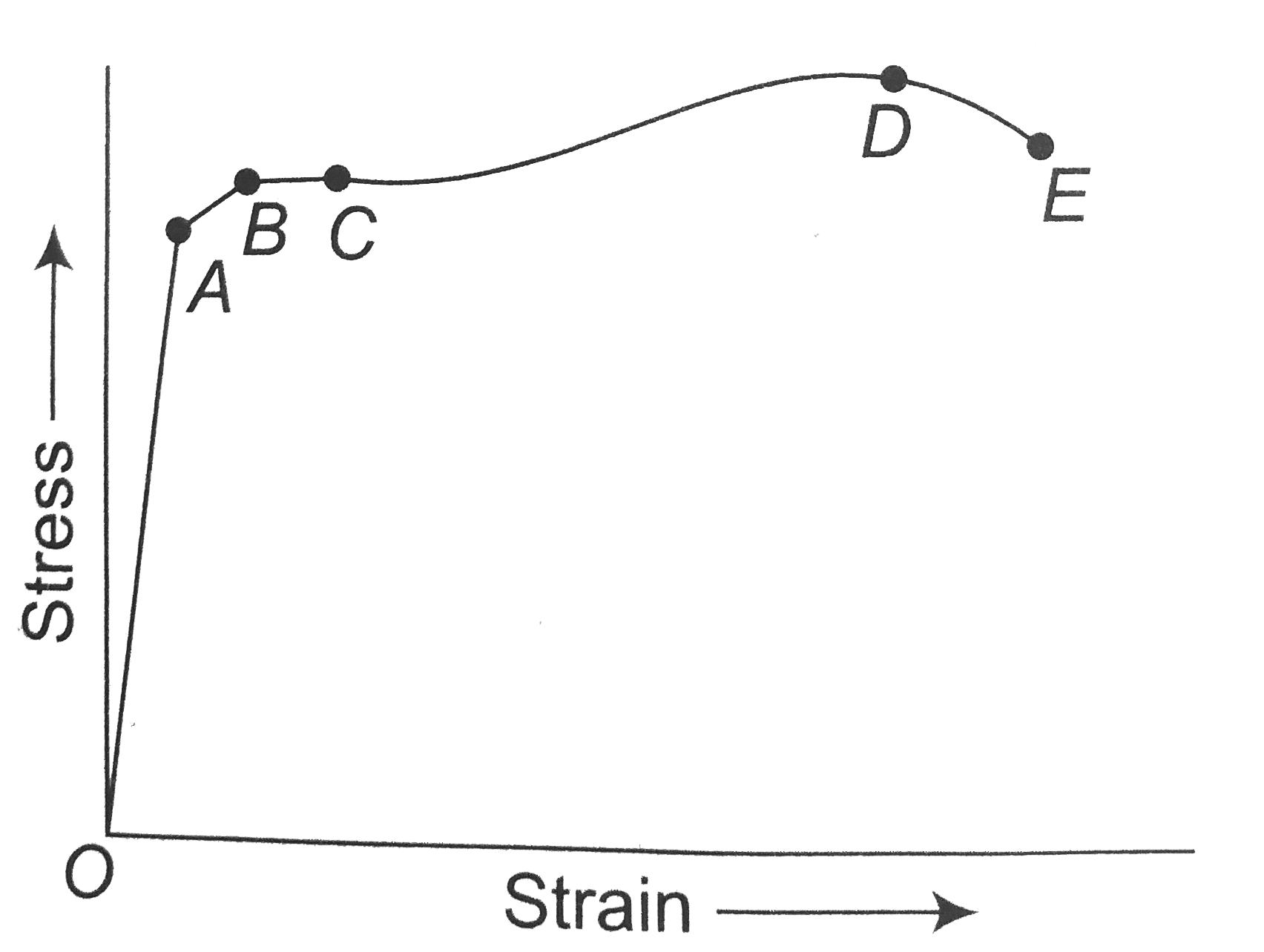 - Question 3 - Select One
The stress strain graph for a metal wire is as shown in the figure. In the graph, the region in which Hooke's law is obeyed, the ultimate strength and fracture are represented byAOA,C,DBOB,D,ECOA,D,EDOB,C,D
The stress strain graph for a metal wire is shown in the fig. Upto the point E, the wire returns to its original state O along the curve EPO, when it is gradually unloaded. Point B corresponds to the fracture of the wire. (a) Upto what point on the curve is Hooke's law obeyed? (this point some times called proportional limits).
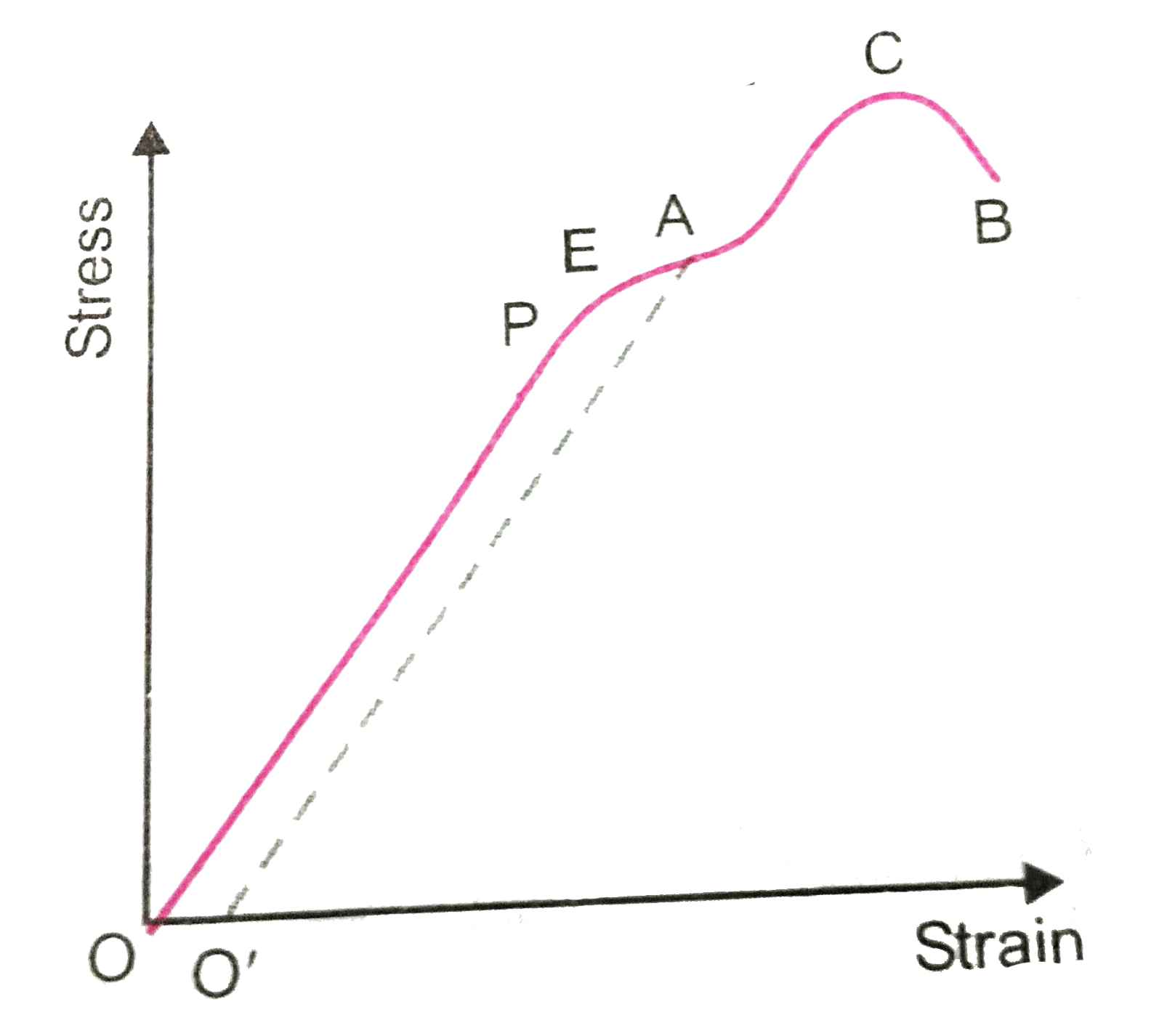
(b) Which point on the curve corresponding to elastic limet or yield point of the wire?
(c ) Indicate teh elastice and plastic regions of the stree-strain graph.
(d) Describe what happens when the wire is loaded upto a stress corresponding to the point A on the graph and then unloaded gradulally. In particular explain the dotted curve.
(e) Wht is peculiar about the protion of the stree- strain graph from C to B? Upto what stress can the wire be subjected with out causing fracture?View SolutionThe following plot shows the variation of potential energy (U) of a system versus position (x). From the graph we can interpret that :
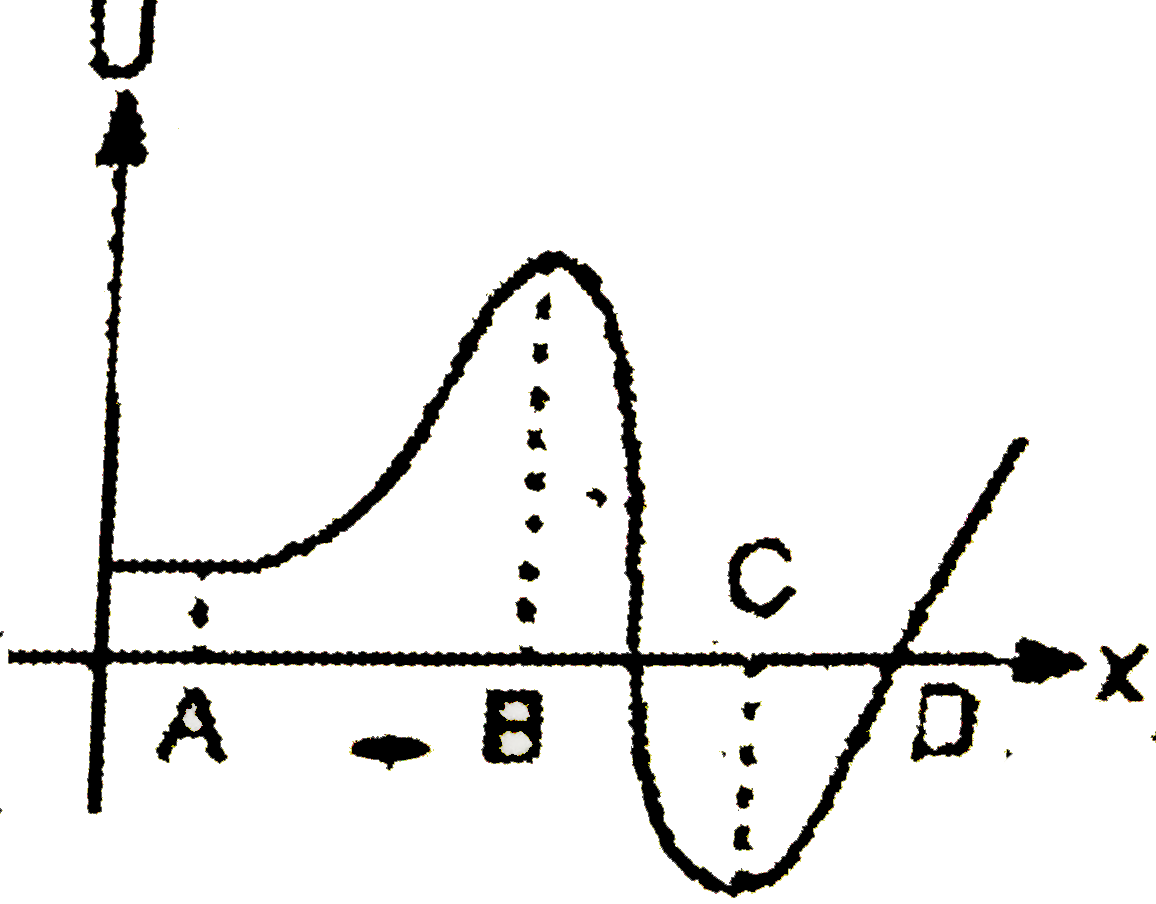
View SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.
Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
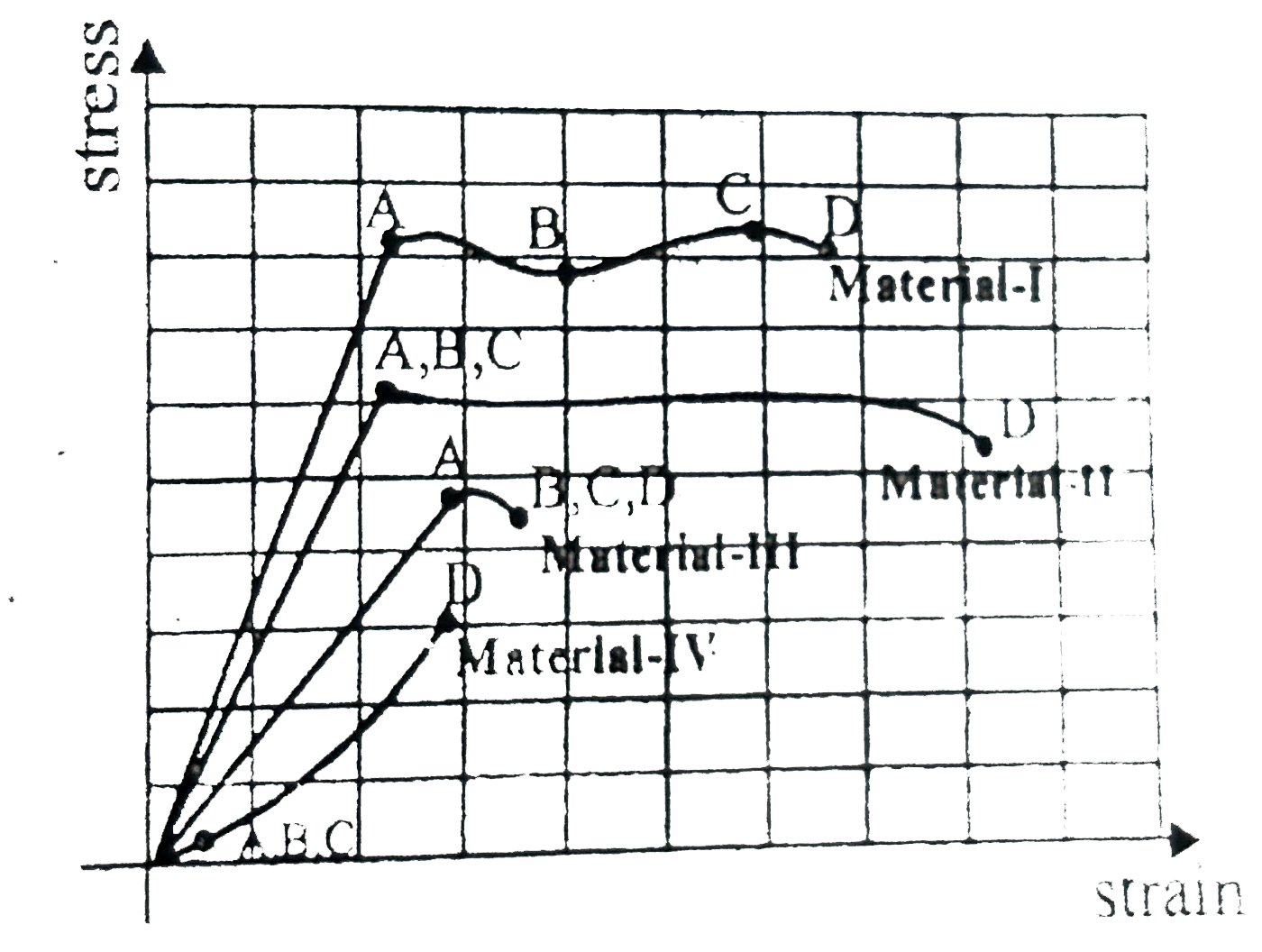
Material which is good for making wires by stretching isView SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.
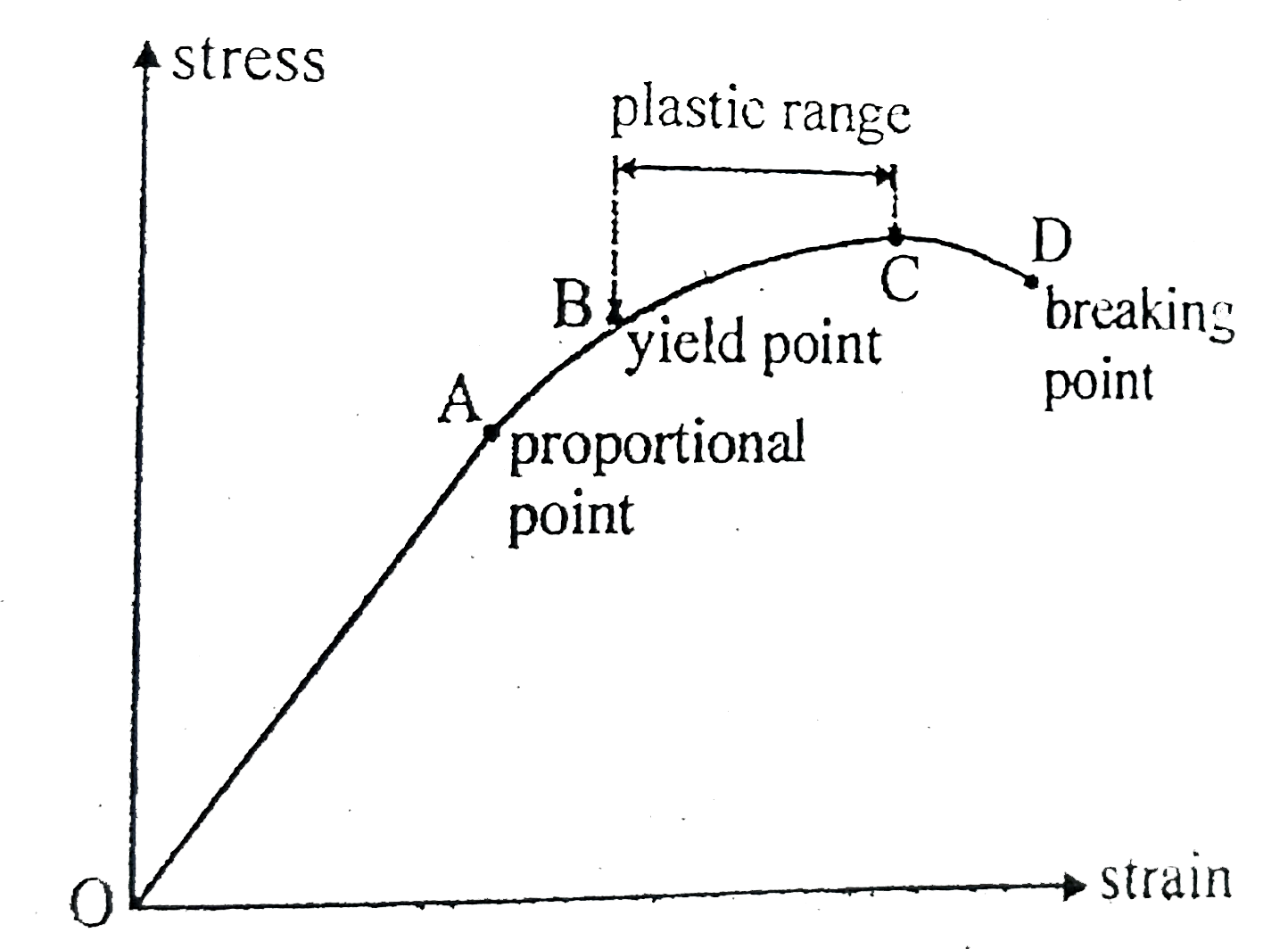
Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
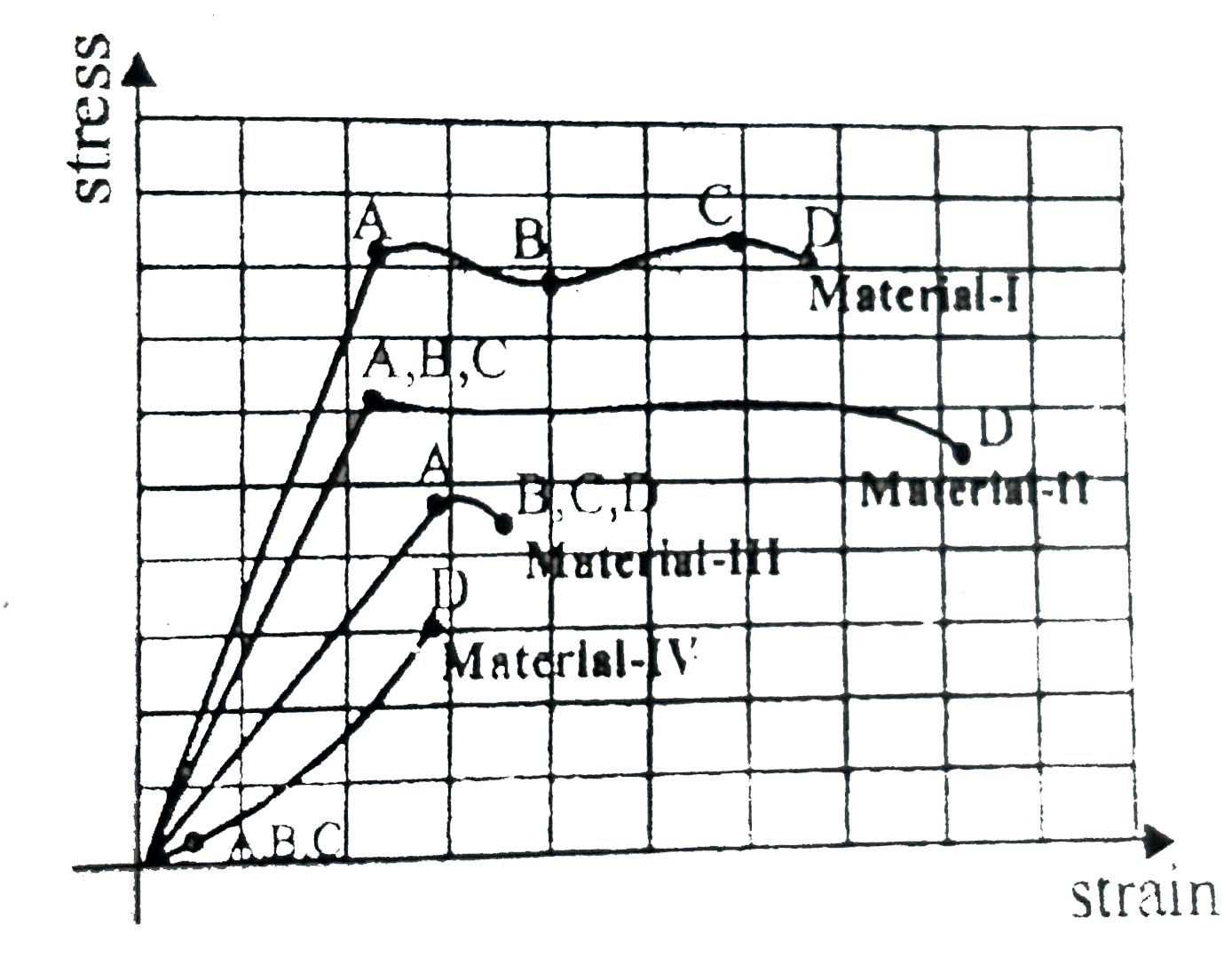
Material which is most brittle isView SolutionFigure shows the relationship between tensile stress and strain for a typical material. Below proportional point A, stress is directly proportional to strain which means Young's moudulus (Y) is a constant. In this region the material obeys Hooke's law.
Provided the strain is below the yield point 'B' the material returns to its original shape and size when the force is removed. Beyond the yield point, the material retains a permancnt deformation after the stress is removed. For stresses beyond the yeld point, the material exhibit plastic flow, which means that it continues to elongate for little increases in the stress. Beyond C a local constriction occurs. The material fractures at D (i.e. breaking point). The graph below shows the stress-strain curve for 4 different materials.
If you bough a new shoe which bites in the beginning and later on fits perfectly, then the material used to making the shoe isView Solution