A circular ring of radius R and mass m made of a uniform wire of cross sectional area A is rotated about a stationary vertical axis passing through its center and perpendicular to the plane of the ring. If the breaking stress of the material of the ring is σb, then determine the maximum angular speed ωmax at which the ring may be rotated without failure.
√2πσAmR
√2πσAmR
3πσAmR
πσA2mR
The correct Answer is:A
Everything element of the ring rotates in a circular path of radius R about the axis of rotation. The radical componenrt of tensionin the wire provides the centripental forces. The figures shows a free body diagram of a small element of a mass fo the ring.
dm=(m/2π)dθ
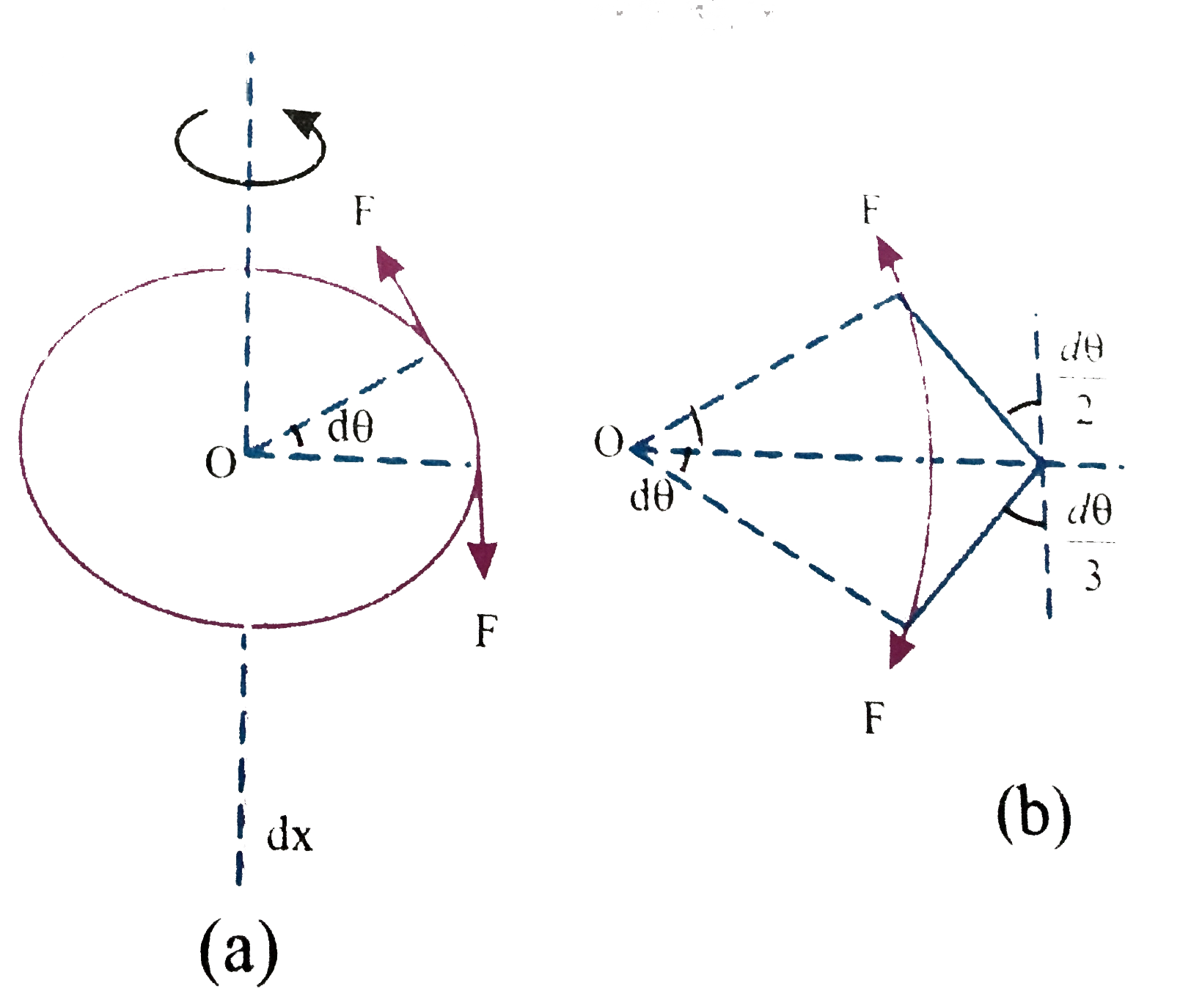
The radical componenet of tension is Fr=2Fsin.dθ2=2F(dθ2)≈Fdθ
Applying Newton's secound law, we get Fdθ=(dm)ω2R
Fdθ=(mdθ2π)ω2R or F=mω2R2π
If the breaking stress is σb then the maximum value of F can be Fmax=σbA
mω2Rmax2π=σbA,ωmax=√2πσ0AmR
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Comprehension-1:
2 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Comprehension-2:
2 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - COMPREHENSION TYPE
11 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE - III
30 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)
31 Videos
Similar Questions
A circular ring of radius R and mass m made of a uniform wire of cross sectional area A is rotated about a stationary vertical axis passing throgh its centre and perpendicular to the plane of the ring. If the breaking stress of the material of the ring is σb, then determine the maximum angular speed ωmax at which the ring may be rotated without failure.
View SolutionA ring of radius r=25cm made of lead wire is rotated about a stationary vertical axis passing through its centre and perpendicular to the plane of the ring. What is the number of rps at which the ring ruptures?
View Solution
Knowledge Check
A ring of mass 10 kg and diameter 0.4m is rotated about an axis passing through its centre and perpendicular to its plane moment of inertia of the ring is
A1.4kgm2B2.4kgm2C0.4kgm2D2kgm2Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
A12mr2ω2Bmrω2Cmr2ω2D12mrω2
Derive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionFrom a ring of mass M and radius R, a 30o sector is removed. The moment of inertia of the remaining portion of the ring, about an axis passing through the centre and perpendicular to the plane of the ring is
View SolutionA ring of radius r made of wire of density ρ is rotated about a stationary vertical axis passing through its centre and perpendicular to the plane of the ring as shown in the figure. Determine the angular velocity (in rad/s) of ring at which the ring breaks. The wire breaks at tensile stress σ. Ignore gravity. Take σ/ρ=4 and r=1m.

View SolutionA ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
View SolutionThe moment of inertia of a thin uniform ring of mass I kg about an axis passing through the centre and perpendicular to the plane of the ring is 0.25 kg m2. Then the diameter of the ring is
View Solution
