A wire is length 2l, radius r and Young's modulus Y pulled perpendicular to its mid point by a distance y. Fina the tesnion in the wire
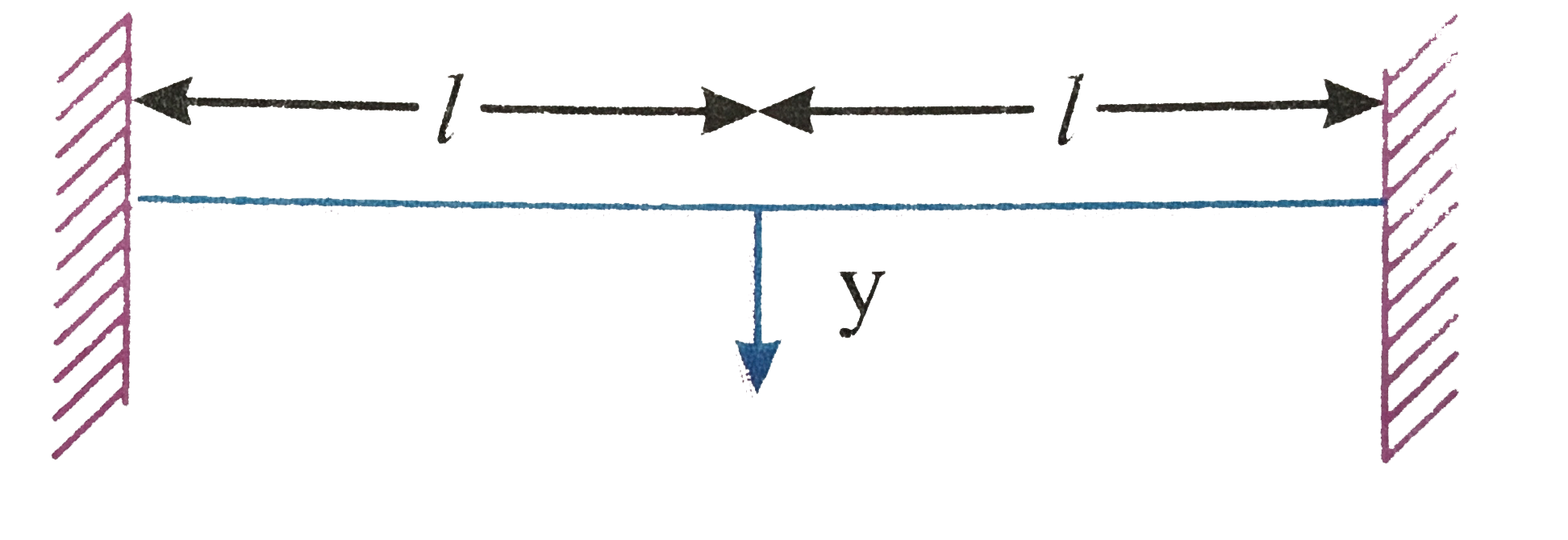
=πr2y2Yl2
=πr2y2Y2l2
=r2y2Y2l2
=r2y2Yl2
The correct Answer is:B
The increases in length of the wire is
Δl=2(√l2+y2−l)=2l⎡⎢⎣(1+y2l2)1/2−1⎤⎥⎦
2ly22l2=y2l(∴y<<l)
Then, strian =e=Δl2l=y22l2, since FA=eY
we have F=eYA=[y22l2](πr2)(Y),=πr2y2Y2l2
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Comprehension-1:2videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Comprehension-2:2videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - COMPREHENSION TYPE11videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE - III30videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)31videos
MOTION IN A PLANE
Similar Questions
Two wire A and B of length l, radius r and length 2l, radius 2r having same Young's modulus Y are hung with a weigth mg, fig. What is the net elonetion in the two wires?
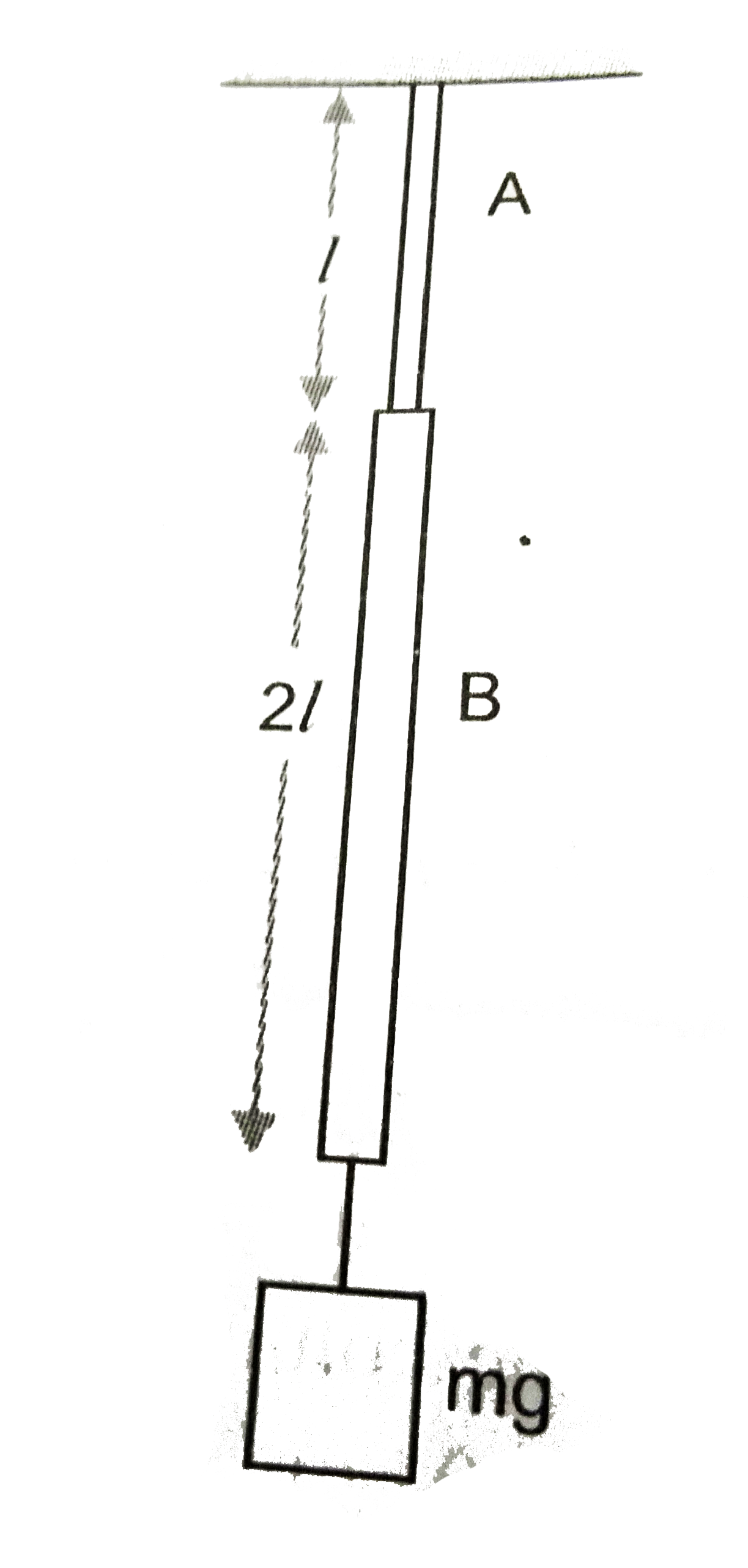 View Solution
View SolutionA wire of length L and area of cross section A is made of a material of Young's modulus Y. If it is stretched by an amount x, the work done is given by
View Solution
Knowledge Check
- Question 1 - Select One
A wire of length L and density ρ and Young's modulus Y is hanging from a support. Find the elongation in the length of wire at which wire will break:
AL2ρgYBL2ρg2YC2L2ρgYDL2ρg4Y - Question 2 - Select One
A wire of length L, density ρ and young's modulus Y produces an elongation 1 in wire by applying load, then frequency of wire is
A12L√YlρlB12L√YLρlC1L√YLρlD1L√YlρL - Question 3 - Select One
A wire of length L and density ρ and Young's modulus Y is hanging from a support. Find the elongation in the length of wire at which wire will break:
AL2ρgYBL2ρg2YC2L2ρgYDL2ρg4Y
A wire of length l and radius r has a weight W and the Young's modulus of elasticity Y. it is suspended vertically from a fixed point. Calculate the increase in length of wire porduced due to its own weight.
View SolutionIf the length of a wire is doubled, then its Young's modulus
View SolutionA metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
View SolutionThe elastic enery stored in a wire of Young's modulus Y is
View SolutionConsider a wire of length L, density ρ and Young's modulus Y . If l is elongation in wire, then frequency of wire is
View Solution

