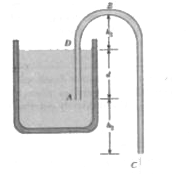
A siphon tube is used to remove liquid from a container as shown in fig. In order to operate the siphon tube, it must initially be filled with the liquid.
(i). Determine the pseed of the liquid through the siphon.
(ii). Determine the pressure at the point C.

(i) Applyiing Bernoulli's equation at point A and D, we get
PA+12rv2A+rgyA=pD+12rv2D+rgyD
Assuming paturn for potential energy at the free surface, we have
yA=0,yD=−(h+y)
pA=pD=patmv2A≈0,vD=v
patm+0+0=patm+12rv2=rg[−(h+y)]
or v=√2g(h+y)
(ii) Applying Bernoulli's equation at A and C, we get
pA+12rv2A+rgyA=pC+12rv2C+rgyC
Here, yC=+H,vC=v (according to the continuity equation)
patm+0+0=pC+12rv2+rgh
or patm=pC+rg(h+y)+rgh
or pC=patm−rg(h+H+y)
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - C.U.Q
117 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Level 1 (C.W)
54 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
Similar Questions
Figure shows a siphon , which is a device for removing liquid from a container . Tube ABC must initially be filled , but once this has been done , liquid will flow through the tube until the liquid surface in the container is level with the tube opening at A . The liquid has density 1000kg/m3 and negligible viscosity . The distances shown are h1=25 cm d = 12 cm and h2=40 cm
Theoretically , what is the greatest possible height h1 that a siphon can lift water ?
View SolutionFigure shows a siphon , which is a device for removing liquid from a container . Tube ABC must initially be filled , but once this has been done , liquid will flow through the tube until the liquid surface in the container is level with the tube opening at A . The liquid has density 1000kg/m3 and negligible viscosity . The distances shown are h1=25 cm d = 12 cm and h2=40 cm
(a) With what speed does the liquid emerge from the tube at C ?
View Solution
Knowledge Check
A U-tube closed at one end is filled with three immiscible liquids having densities ρ,3pand8ρ as shown in figure. The pressure at point C inside the tube is:
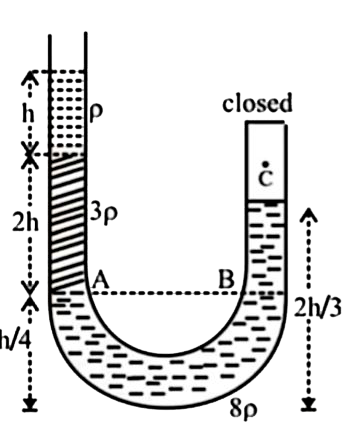 AP0+hρg3BP0+11hρg3CP0+2hρg3DP0+hρg
AP0+hρg3BP0+11hρg3CP0+2hρg3DP0+hρgA glass tube int the form of an equilateral triangle of uniform cross-section is as shown in figure. It lies in the vertical plane, with base horizontal . The tube is filled with equal volumes of three immiscible liquid whose densities are in arithmetic progession. Determine the length x as shown in figure
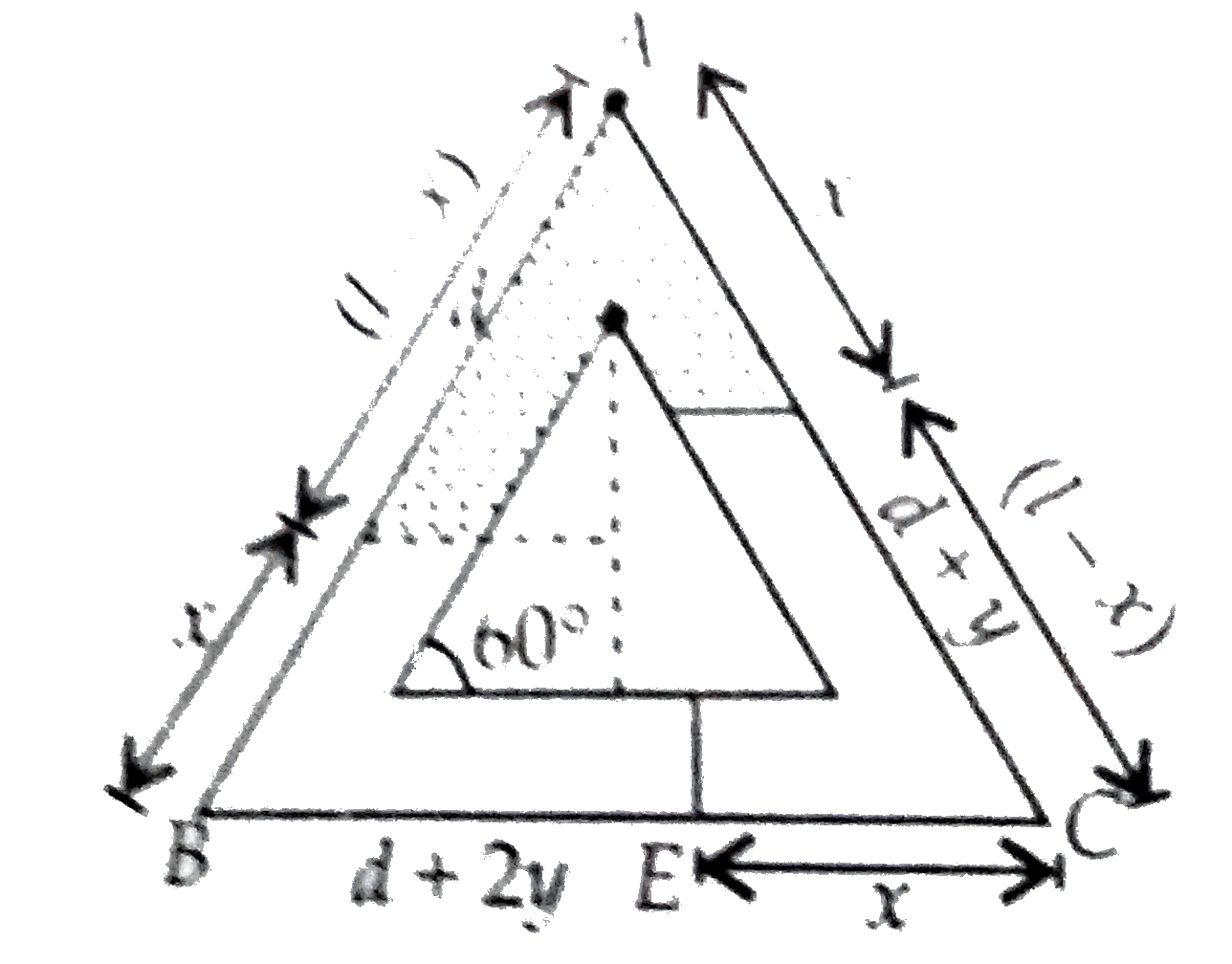 A3 lB2 lCl/3Dl/2
A3 lB2 lCl/3Dl/2A thief steals four gallons of liquid soap kept in a train compartment's bathroom from a container that is full of liquid soap. He then fills it with water to avoid detection. Unable to resist the temptation he steals 4 gallons of the mixture again, and fills it with water. When the liquid soap is checked at a station it is found that the ratio of the liquid soap now left in the container to the water in it is 36 : 13. What was the initial amount of the liquid soap in the container if it is known that the liquid soap is neither used nor augmented by anybody else during the entire period?
A7 gallonsB14 gallonsC21 gallonsD28 gallons
Figure shows a siphon , which is a device for removing liquid from a container . Tube ABC must initially be filled , but once this has been done , liquid will flow through the tube until the liquid surface in the container is level with the tube opening at A . The liquid has density 1000kg/m3 and negligible viscosity . The distances shown are h1=25 cm d = 12 cm and h2=40 cm
If the atmospheric pressure is 1.0×105Pa, what is the pressure in the liquid at the topmost point B ?
View SolutionA siphon tube is discharging a liquid of specific gravity 0.9 from a reservoir as shown in the figure.

(a) Find the velocity of the liquid through the siphon.
(b) Find the pressure at the highest point B.
(c ) Find the pressure at point C.
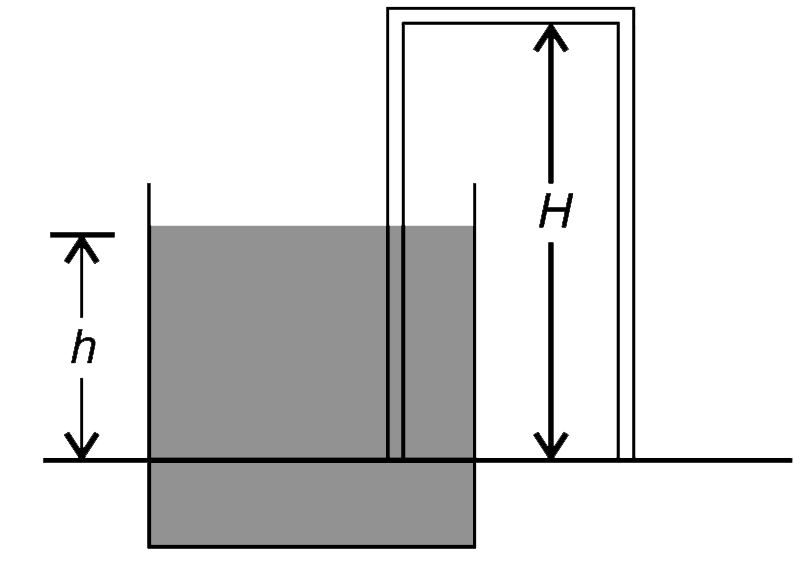
View SolutionA siphon is used to drain water (density=ρ) from a wide tank. The inlet and outlet mouth of the siphon are at the same horizontal level and the highest point of the siphon tube is at a height H from the mouth of the tube. Height of water in the tank above the tube mouth is h (see fig). Atmospheric pressure is P0.
(a) Will the water drain out in this siphon? if yes, at what speed (V)?
(b) Find pressure at the top of the siphon tube (call in P)
(c) Find pressure just inside the left mouth of the tube.
(d) If left part of the tube is slightly cut short, without disturbing anything else, what effect it will have on V and P?
(e) If the right end of the tube is lowered by adding more lenght of tube, it was observed that flow stops when lenght of right limb of the tube becomes H0. Find H0.
View SolutionWhen 100 drops of a liquid P is added into a liquid Q the volume of the liquid in the container which is initially filled with liquid Q doubled. Determined density of the mixture if density of the liquids P and Q are 1.5 g cm ^(-3) and 1.3 g cm^(-3), respectively
View SolutionConsider a liquid at rest in a container which opens into atmosphere. At any point A at a depth h below the surface of the liquid,
(i) the gauge pressure at point A is ρgh.
(ii) the gauge pressure at point a is Pa+ρgh.
(iii) The pressure at point A is ρgh.
(iv) The pressure at point A is Pa +ρgh.
The correct alternative is
View Solution
