A tank full of water has a small hole at the bottom. If one-fourth of the tank is emptied in t1 seconds and the remaining three-fourths of the tank is emptied in t2 seconds. Then the ratio t1t2 is
√3
√2
1√2
2√3−1
The correct Answer is:D
To solve the problem, we need to determine the ratio t1t2 based on the time taken to empty different portions of the tank through a small hole at the bottom.
1. Understanding the Problem:
- We have a tank full of water with a small hole at the bottom.
- One-fourth of the tank is emptied in t1 seconds.
- The remaining three-fourths of the tank is emptied in t2 seconds.
2. Using Torricelli's Law:
- The velocity v of the water flowing out of the hole is given by Torricelli's theorem:
v=√2gh
where h is the height of the water above the hole.
3. Setting Up the Equations:
- Let the total height of the tank be H.
- When one-fourth of the tank is emptied, the height of the water left in the tank is 3H4.
- When three-fourths of the tank is emptied, the height of the water left in the tank is 0.
4. Deriving the Time for t1:
- The volume flow rate Q through the hole is given by:
Q=A⋅v=A⋅√2gh
where A is the area of the hole.
- The change in height dh over time dt can be expressed as:
A⋅√2gh=−A⋅dhdt
- Rearranging gives:
dh√h=−kdt
where k is a constant.
5. Integrating for t1:
- Integrating from h=H to h=3H4:
∫3H4Hdh√h=−k∫t10dt
- The left side integrates to:
2(√h)∣∣∣3H4H=2(√3H4−√H)=2(√3H2−√H)=√3H−2√H
- Thus, we have:
t1=k(√3H−2√H)
6. Deriving the Time for t2:
- Now, integrating from h=3H4 to h=0:
∫03H4dh√h=−k∫t2t1dt
- The left side integrates to:
2(√h)∣∣∣03H4=0−2(√3H2)=−√3H
- Thus, we have:
t2=k√3H
7. Finding the Ratio t1t2:
- Now we can find the ratio:
t1t2=k(√3H−2√H)k√3H=√3H−2√H√3H=1−2√H√3H=1−2√3
- Simplifying gives:
t1t2=√H√3H−1=2√3−1
8. Final Result:
- The final ratio t1t2 is:
t1t2=2√3−1
- Thus, the answer is 2√3−1.
- We have a tank full of water with a small hole at the bottom.
- One-fourth of the tank is emptied in t1 seconds.
- The remaining three-fourths of the tank is emptied in t2 seconds.
- The velocity v of the water flowing out of the hole is given by Torricelli's theorem:
v=√2gh
where h is the height of the water above the hole.
- Let the total height of the tank be H.
- When one-fourth of the tank is emptied, the height of the water left in the tank is 3H4.
- When three-fourths of the tank is emptied, the height of the water left in the tank is 0.
- The volume flow rate Q through the hole is given by:
Q=A⋅v=A⋅√2gh
where A is the area of the hole.
- The change in height dh over time dt can be expressed as:
A⋅√2gh=−A⋅dhdt
- Rearranging gives:
dh√h=−kdt
where k is a constant.
- Integrating from h=H to h=3H4:
∫3H4Hdh√h=−k∫t10dt
- The left side integrates to:
2(√h)∣∣∣3H4H=2(√3H4−√H)=2(√3H2−√H)=√3H−2√H
- Thus, we have:
t1=k(√3H−2√H)
- Now, integrating from h=3H4 to h=0:
∫03H4dh√h=−k∫t2t1dt
- The left side integrates to:
2(√h)∣∣∣03H4=0−2(√3H2)=−√3H
- Thus, we have:
t2=k√3H
- Now we can find the ratio:
t1t2=k(√3H−2√H)k√3H=√3H−2√H√3H=1−2√H√3H=1−2√3
- Simplifying gives:
t1t2=√H√3H−1=2√3−1
- The final ratio t1t2 is:
t1t2=2√3−1
- Thus, the answer is 2√3−1.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Level 329videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Statement Type Questions16videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Level 1 (C.W)54videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q13videos
MATHEMATICAL REVIEW & PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
Similar Questions
A tank full of water has a small hole at its bottom. Let t1 be the time taken to empty first one third of the tank and t2 be the time taken to empty second one third of the tank and t3 be the time taken to empty rest of the tank then
(a). t1=t2=t3
(b). t1>t2>t3
(c). t1<t2<t3
(d). t1>t2<t3View SolutionA tank is filled with a liquid upto a height H, A small hole is made at the bottom of this tank Let t1 be the time taken to empty first half of the tank and t2 time taken to empty rest half of the tank then find t1t2
View Solution
Knowledge Check
- Question 1 - Select One
A tank full of water has a small hole at its bottom. Let t1 be the time taken to empty the first half of the tank and t2 be the time needed to empty the rest half of the tank, then
At1=t2Bt1>t2Ct1<t2Dt1=0.523t2 - Question 2 - Select One
Choose the most appropriate option.
A tank is filled with a liquid upto a height H. A small hole is made at the bottom of this tank. Consider t1 be the time taken to empty first half of the tank and t2 be the time taken to empty rest half of the tank. Then, determine the ratio t1t2.A1.33B1.5C2D0.414 - Question 3 - Select One
A tank has a hole at its bottom. The time needed to empty the tank from level h1 to h2 will be proportional to
Ah1−h2Bh1+h2C√h1−√h2D√h1+√h2
An open tank of cross sectional area A contains water up to height H. It is kept on a smooth horizontal surface. A small orifice of area A0 is punched at the bottom of the wall of the tank. Water begins to drainout. Mass of the empty tank may be neglected.
(i) Prove that the tank will move with a constant acceleration till it is emptied. Find this acceleration.
(iii) Find the find speed acquired by the tank when it is completely empty.
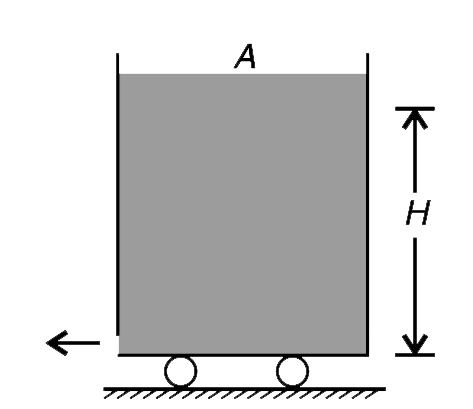 View Solution
View SolutionA large open tank is filled with water upto a height H. A small hole is made at the base of the tank. It takes T1 time to decrease the height of water to H/n(ngt1) and it takes T2 time to take out the remaining water. If T1=T2, then the value of n is
View SolutionA pipe can fill a tank in 12 hours. By mistake another pipe that empties the tank is left open and tank is filled in 16 hours. If the tank is full, how much time will the second pipe take to empty it?
View SolutionA leak in the bottom of a tank can empty the full tank in 6 hours. An inlet pipe fills water at the rate of 4 litres a minute. When the tank is full, the inlet is opened and due to the leak the tank is empty in 8 hours. Find the capacity of the tank.
View SolutionA large tank is filled with water to a height H. A small hole is made at the base of the tank. It takes T1 time to decrease the height of water to Hη(η>1), and it takes T2 time to take out the rest of water. If T1=T2, then the value of η is
View Solution

