Statement I: When a body floats such that its parts are immersed into two immiscible liquids, then force exerted by liquid 1 is of magnitude ρ1v1g.
Statement II: Total buoyant force =ρ1v1g+ρ2v2g.

Statement-I is true, statement-2 true and statements-2 is a correct explanation for statements-2
Statement 1 is true, statement 2 is true, statement-2 is not a correct explanation for statement 2
Statement 1 is true, statement 2 is false
Statement 1 is false, statement 2 is true
The correct Answer is:D
Buoyant force involves volume of only submerged body.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - More Than One Alternative Type Question
32 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Comprehension Type Questions
40 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Level 3
29 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
Similar Questions
A body of density ρfloats with a volume V1 of its total volume V immersed in one liquid of density ρ1 and with the remainder of volume V2 immersed in another liquid of density ρ2, where ρ1>ρ2. Find the relative volumes immersed in two liquids.
View SolutionThe light cone is in equilibrium under the action of hydrostatic forces of two liquids of densities ρ1 and ρ2. Find ρ1/ρ2. Find ρ1 and ρ2.
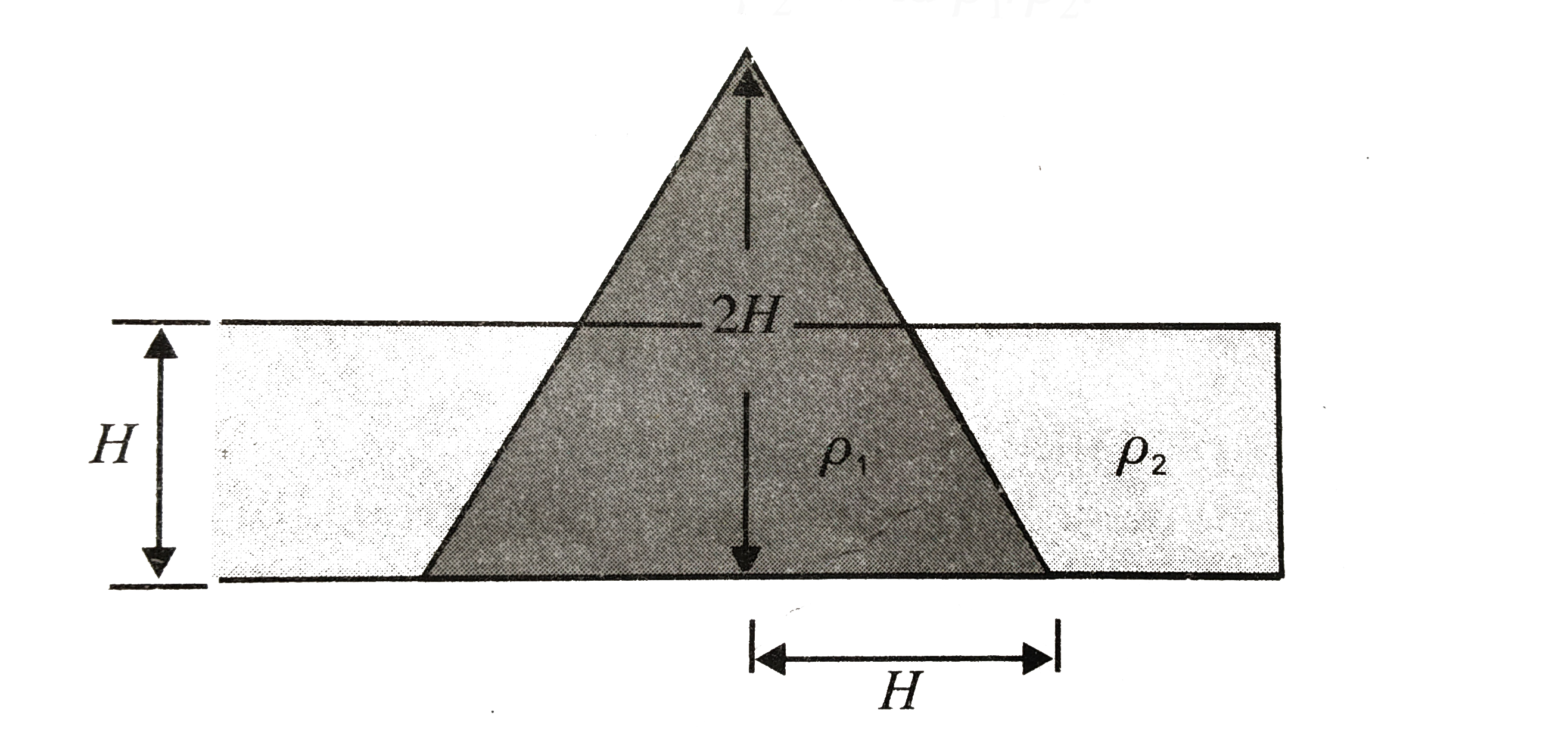
View Solution
Knowledge Check
A solid uniform ball of volume V floats on the interface of two immiscible liquids (see the figure). The specific gravity of the upper liquid is ρ1 and that of lower one is ρ2 and the specific gravity of ball is ρ(ρ1>ρ>ρ2) The fraction of the volume the ball in the u of upper liquid is
 Aρ2ρ1Bρ2−ρρ2−ρ1Cρ−ρ1ρ2−ρ1Dρ1ρ2
Aρ2ρ1Bρ2−ρρ2−ρ1Cρ−ρ1ρ2−ρ1Dρ1ρ2A solid uniform ball having volume V and density ρ floats at the interface of two unmixable liquids as shown in the figure. The densities of the upper and the lower liquids are ρ1 and ρ2 respectively, such that ρ1<ρ<ρ2 . What fraction of the volume of the ball will be in the lower liquid ?
 Aρ−ρ2ρ1−ρ2Bρρ1−ρ2Cρ1−ρρ1−ρ2Dρ1−ρ2ρ2
Aρ−ρ2ρ1−ρ2Bρρ1−ρ2Cρ1−ρρ1−ρ2Dρ1−ρ2ρ2A solid uniform ball having volume V and density ρ floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are ρ1 and ρ2 respectively, such that ρ1<ρ<ρ2. What fractio9n of the volume of the ball will be in the lower liquid.
 Aρ−ρ2ρ1−ρ2Bρ1ρ1−ρ2Cρ1−ρρ1−ρ2Dρ1−ρ2ρ2
Aρ−ρ2ρ1−ρ2Bρ1ρ1−ρ2Cρ1−ρρ1−ρ2Dρ1−ρ2ρ2
A plank of area of cross-section A and mass m is immersed in two immiscible liquids such that L4 part of the plank is immersed in liquid of density 2ρ and 3L4 part immersed in liquid of density ρ. The period of oscillation of the plank if it is slightly depressed downwards is 2π√mβAρg. Find β.
'(##CEN_KSR_PHY_JEE_C16_E01_033_Q17##)'
View SolutionA body of density ρ floats with volume V1 of its total volume V immersed in a liquid of density ρ1 and with the remainder of volume V2 immersed in another liquid of density ρ2 where ρ1>ρ2. Find the volume immersed in two liquids. (V1 and V2).
View SolutionThe ratio of buoyant forces experienced by a solid body when immersed in two liquids whose relative densities are 1 and 0.5, respectively, is 2 : 1
View SolutionA body of volume V and density d is completely immersed in a liquid of density p. Then the apparent weight of the body will be:
View SolutionA solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densityes ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
View Solution
