The light cone is in equilibrium under the action of hydrostatic forces of two liquids of densities ρ1 and ρ2. Find ρ1/ρ2. Find ρ1 and ρ2.

The correct Answer is:516
The upward thrust due to liquid 1= downward thrust due to liquid 2.
F1=F2

F1=[ρ1πR2(2H)g−ρ1(πR2(2H3))]g=4πR2Hρ1g3
F2=Vρ2g,whereV= volume of the double shaded position
=πR2H=⎡⎢
⎢
⎢⎣πR2(2H)3−π(R2)2H3⎤⎥
⎥
⎥⎦
=512πR2H=512πH3
Then ρ1ρ2=516
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Single Correct95videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct15videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.410videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
Similar Questions
V1 and V2 are the velocities of sound at the same temperature in two monoatomic gases of densities ρ1 and ρ2 respectively.If ρ1ρ2=14 then the ratio of velocities V1 and V2 is
View SolutionEqual masses of two substance of densities ρ1andρ2 are mixed together. What is the density of the mixture?
View Solution
Knowledge Check
- Question 1 - Select One
A solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densityes ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
A(rho-rho_(1))/(rho_(2)-rho)Bρ2−ρρ−ρ1C(rho+rho_(1))/(rho+rho_(2))D(rho+rho_(2))/(rho+rho_(1)) - Question 2 - Select One
A thin uniform tube is bent into a circle of radius r in the vertical plane. Equal volumes of two immiscible liquids, whose densities are ρ1 and ρ2(ρ1>ρ2) fill half the circle. The angle θ between the radius vector passing though the common interface and the vertical is :
Aθ=tan−1'π2(ρ2ρ1)Bθ=tan−1'π(ρ1ρ2)Cθ=tan−1'π2(ρ1+ρ2ρ1−ρ2)Dθ=tan−1'[π2(ρ1+ρ2ρ1−ρ2)] - Question 3 - Select One
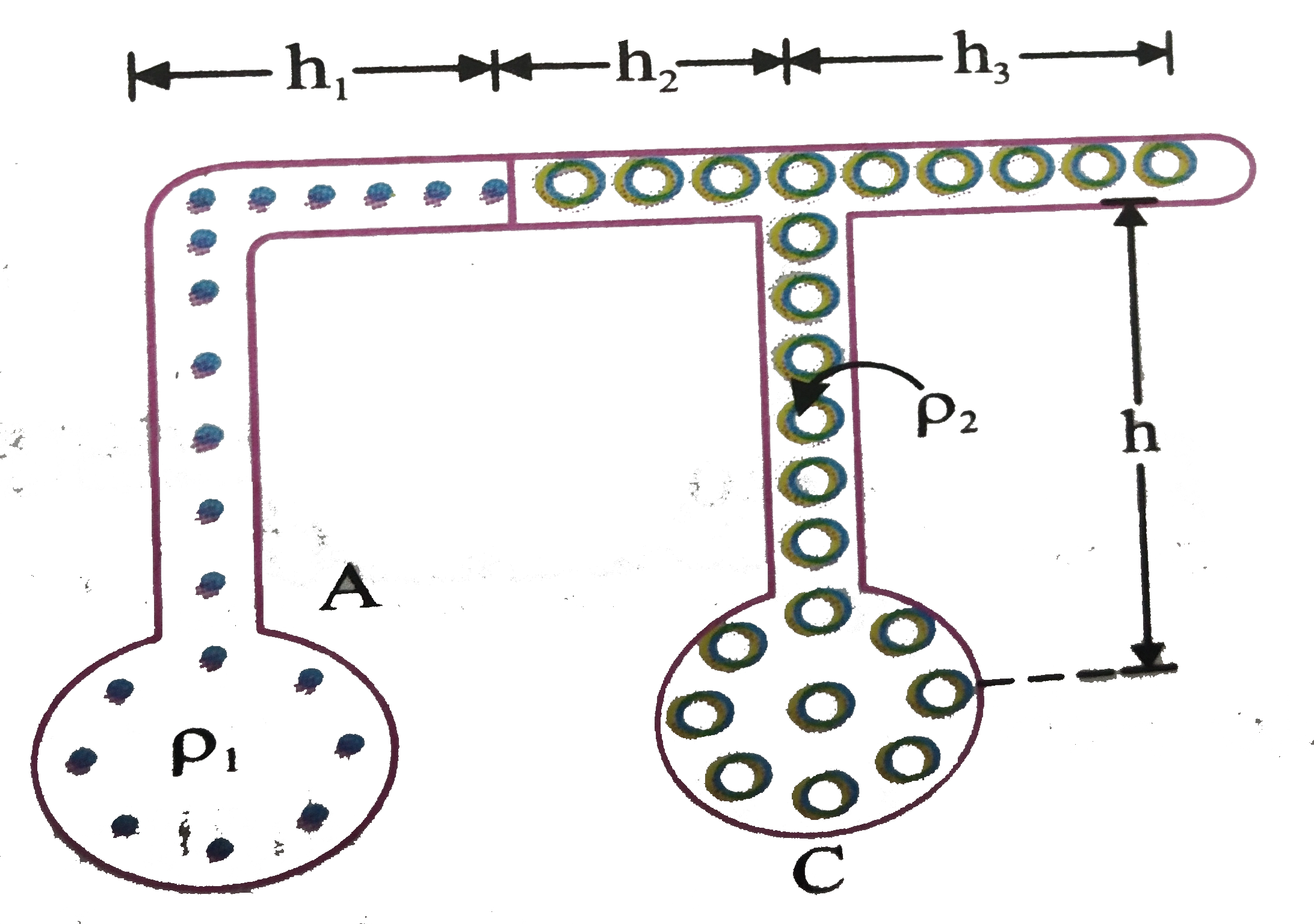
The difference in pressures in bulbs A and C having fluids of densities ρ1 and ρ2 when tube B is horizontal will beA(ρ2−ρ1)ghBρ2g(h2+h3)−ρ1gh1Cρ2g(h+h2)−−ρ−(1)g(h+h1)D(ρ1−ρ2)gh
A uniform sphere of density ρ floats at the interface of two liquids of densities ρ1 and ρ2(>ρ1) The sphere has 23 rd of vertical diameter in denser liquid and remaining part in the other liquid.If aρ=bρ1+cρ2 then b+c-a=_______.
View SolutionA cube of 1 kg is floating at the interface of two liquids of density ρ1=3/4gm/cm3andρ2=2.5gm/cm3 The cube has (3/5)th part in ρ2 and (2/5)th part in ρ1 .Find the density of the cube .
 View Solution
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
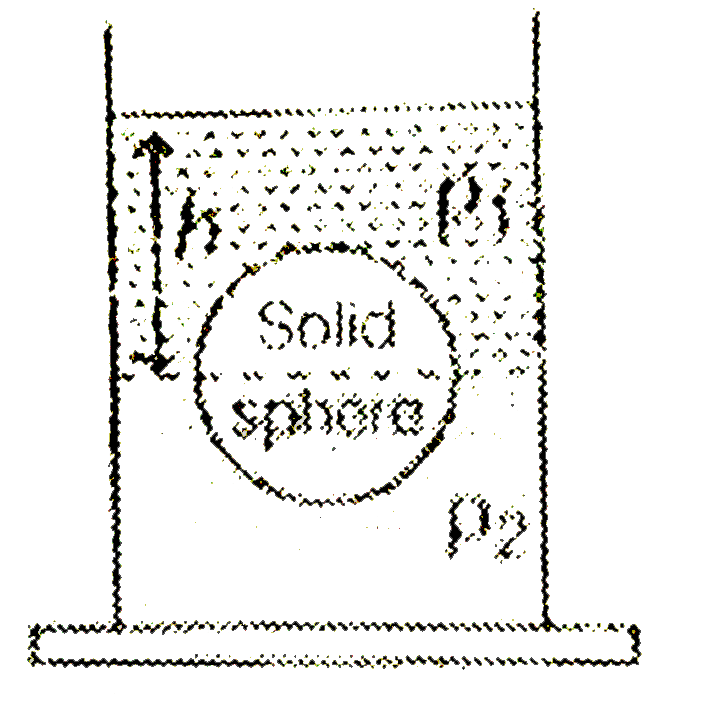 View Solution
View SolutionA narrow U-tube placed on a horizontal surface contains two liquids of densities ρ1 and ρ2 . The columns of the liquids are indicated in the figure. The ratio ρ1ρ2 is equal to :
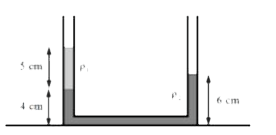 View Solution
View SolutionThe densities at points A and B are ρ0 and 3ρ02. Find the value of x on P-axis.
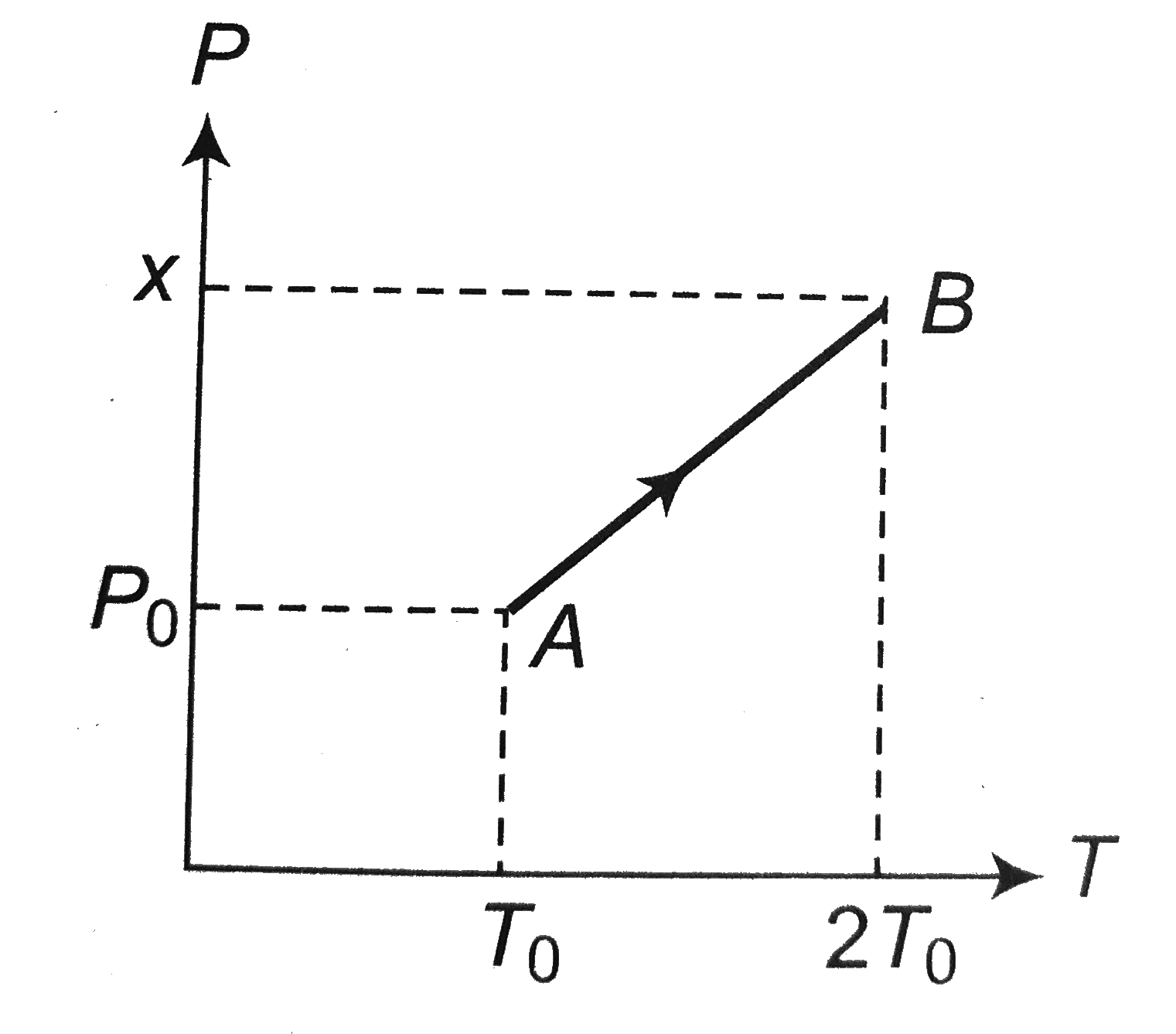 View Solution
View Solution

