A large open tank has two holes in the wall. The top hole is a square hole of side L at a depth y from the surface of water. The bottom hole is a circular hole of radius R at a depth 4y from surface of water . If R=L/2√π, find the correct graph. V1 and V2 are the velocities in top and bottom holes. Area of the square & curcular holes are a1 and a2
The correct Answer is:B
R=L/2√π
4πR2=L2 or 4πR2√2gy=L2√2gy
or 2a2V2=a1V1 where a1=L2,a2=πR2
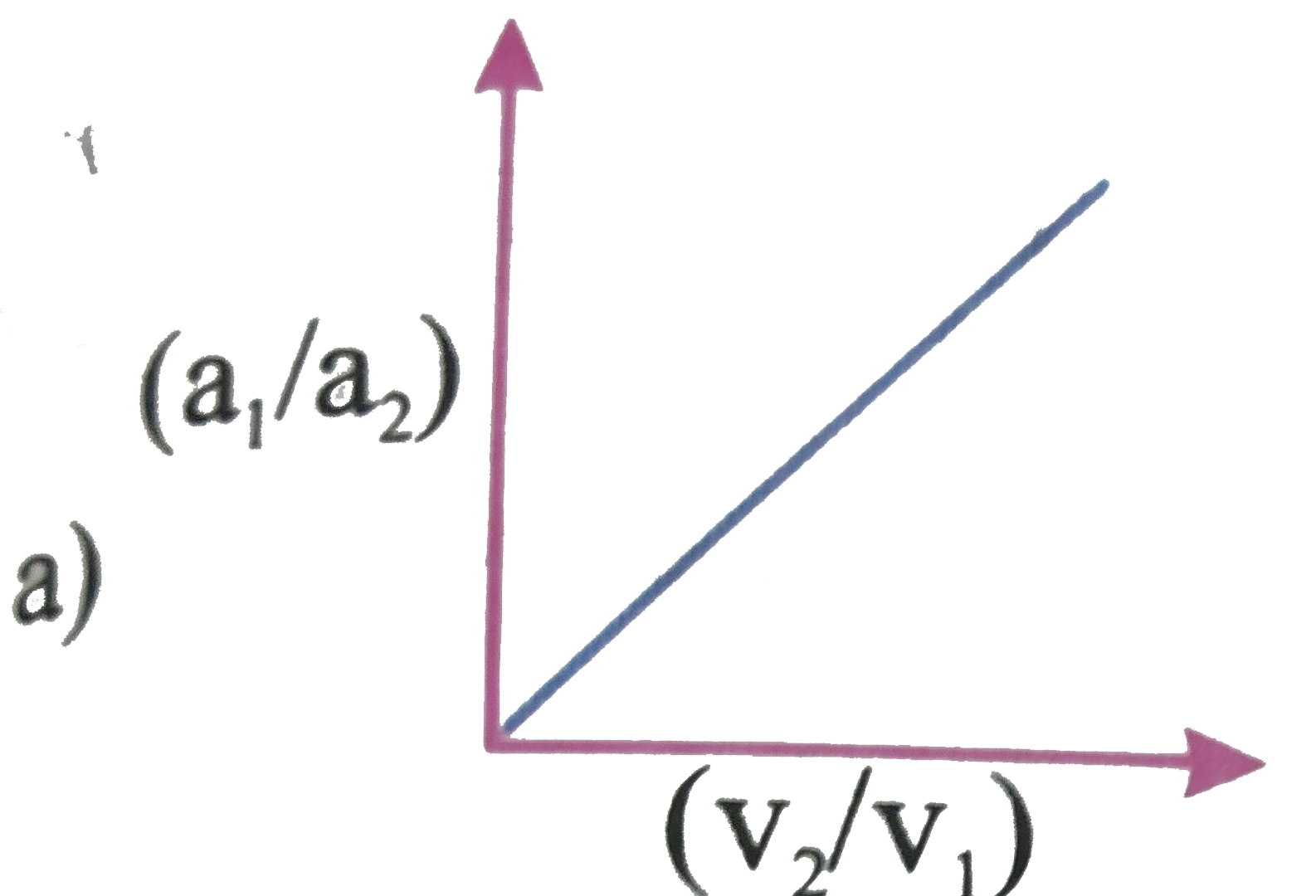
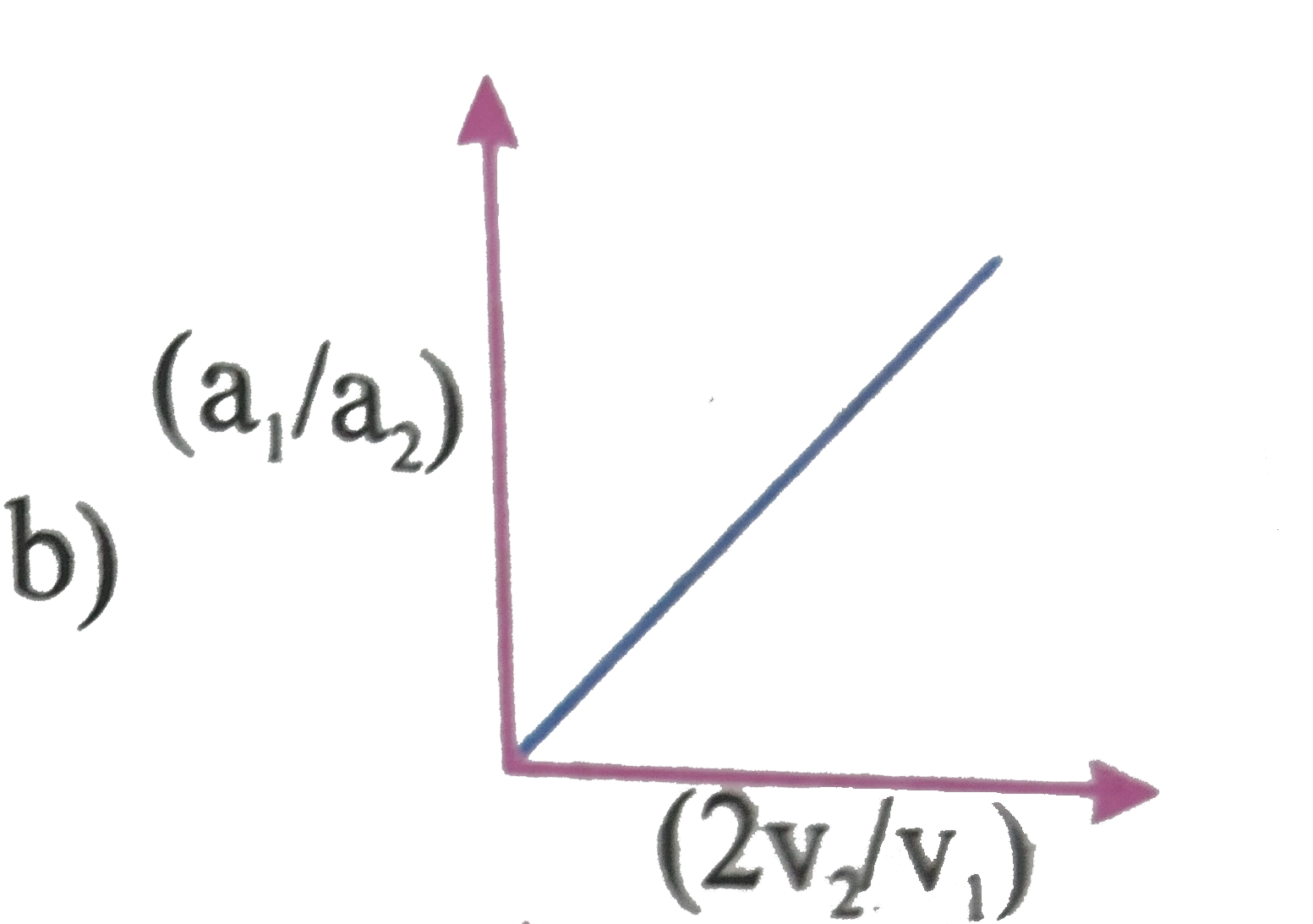
V1=√2gy,V2=√2g(4y), so (a1a2)=(2V2V1)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - integer Type Questions25videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Level 1 (H.W)55videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Paragraph Type Questions5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q13videos
MATHEMATICAL REVIEW & PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
Similar Questions
A large open tank has two holes in the wall. One is a square hole of side L at a depth h from the top and the other is a circular hole of radius r at a depth 4h from the top. Whwn the tank is completely filled with water, the quantity of water flowing out per second from both the holes are the same. What is the value of r?
View SolutionA tank is filled to a height H. The range of water coming out of a hole which is a depth H/4 from the surface of water level is
View Solution
Knowledge Check
- Question 1 - Select One
A large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
AL√2πB2πLCL√2πDL2π - Question 2 - Select One
A large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
A(a) L√2πB(b) 2πLC(c) LD(d) L2π - Question 3 - Select One
A large open tank has two holes in its wall. Ine is a square hole of side a at a depath of x from the top and the other is a cirular hle of radius r at a depth 4x from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then r is equal to
A2πaBaCa2πDa√2π
There is a circularr hole in a square copper plate. If the plate is heated then the radius of the circular hole will
View SolutionA water tank has a hole in its wall at a distance of 40 m below the free surface of water. Compute the velocity of flow of water from the hole. If the radius of the hole is 1 mm. find the rate of flow of water
View SolutionThe height of the water in a tank is H. The range of the liquid emerging out from a hole in the wall of the tank at a depth 3H4 from the upper surface of water, will be
View SolutionA cylinderical vessel is filled with water up to height H. A hole is bored in the wall at a depth h from the free surface of water. For maximum range h is equal to
View SolutionA water tank, open to the atmosphere, has a leak in it in the form of a circular hole, located at a height h below the open surface of water. The velocity of the water coming out of the hole is :
View Solution

