A wooden cylinder of length L is partly submerged in a liquid of specific gravity ρ1 with nth (n<1) part of it inside the liquid. Another immiscible liquid of density ρ2 is poured to completely submerge the cylinder. Density of cylinder ρ is the geometric mean of the densities of the two liquid.
Similarly as above, find the time period of small oscillations above the mean position.
π[nLg]12
π[Lng]12
π[(n−1)Lg]12
π[nL(n−1)g]12
The correct Answer is:A
Restoring force =−Axρ1g
Alρa=−Axρn.g,xa=−nLg
T22=π√∣∣xa∣∣=π[nLg]12
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Paragraph Type Questions
5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Single Answer Questions
108 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - More Than One Alternative Type Question
32 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
Similar Questions
A wooden cylinder of length l floats vertically in a liquid of specific gravity ρ with (13)rd part of its length submerged. Another liquid that is immiscible with the previous liquid is poured into it, to just completely submerge the cylinder. If the density of the liquid at the bottom, density of cylinder and density of upper liquid are in G.P., find the fraction of the cylinder submerged in lower liquid.
View SolutionA body weighs W1 in a liquid of density ρ1 and W2 in a liquid of density ρ2. What is the weight of body in a liquid of density ρ3?
View Solution
Knowledge Check
A wooden cylinder of length L is partly submerged in a liquid of specific gravity ρ1 with nth (n<1) part of it inside the liquid. Another immiscible liquid of density ρ2 is poured to completely submerge the cylinder. Density of cylinder ρ is the geometric mean of the densities of the two liquid.
When the cylinder is slightly depressed and released, it oscillates. let there be a mean position. find the time period of small oscillations below thee mean positionAπ[(n+a)Lg(n−1)]12Bπ[n2Lg(1−n)2]12Cπ[nLg(n2−1)]1/2Dπ[nLg(1−n2)]12A wooden cylinder of length L is partly submerged in a liquid of specific gravity ρ1 with nth(n<1) part of it inside the liquid. Another immiscible liquid of density ρ2 is poured to completely submerge the cylinder. Density of cylinder ρ is the geometric mean of the densities of the two liquid.
Express the density of upper liquid in terms of density of cylinderAρnBρnCn(n+1)DnoneA wooden cylinder of length L is partly submerged in a liquid of specific gravity ρ1 with nth (n<1) part of it inside the liquid. Another immiscible liquid of density ρ2 is poured to completely submerge the cylinder. Density of cylinder ρ is the geometric mean of the densities of the two liquid.
Calculate the fraction of the cylinder submerged in the lower liquid after the upper liquid is poured in the vesselAn(n+1)B(n−1)(n+1)Cn(n−1)(n+1)Dn(n−1)(n+1)
A vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
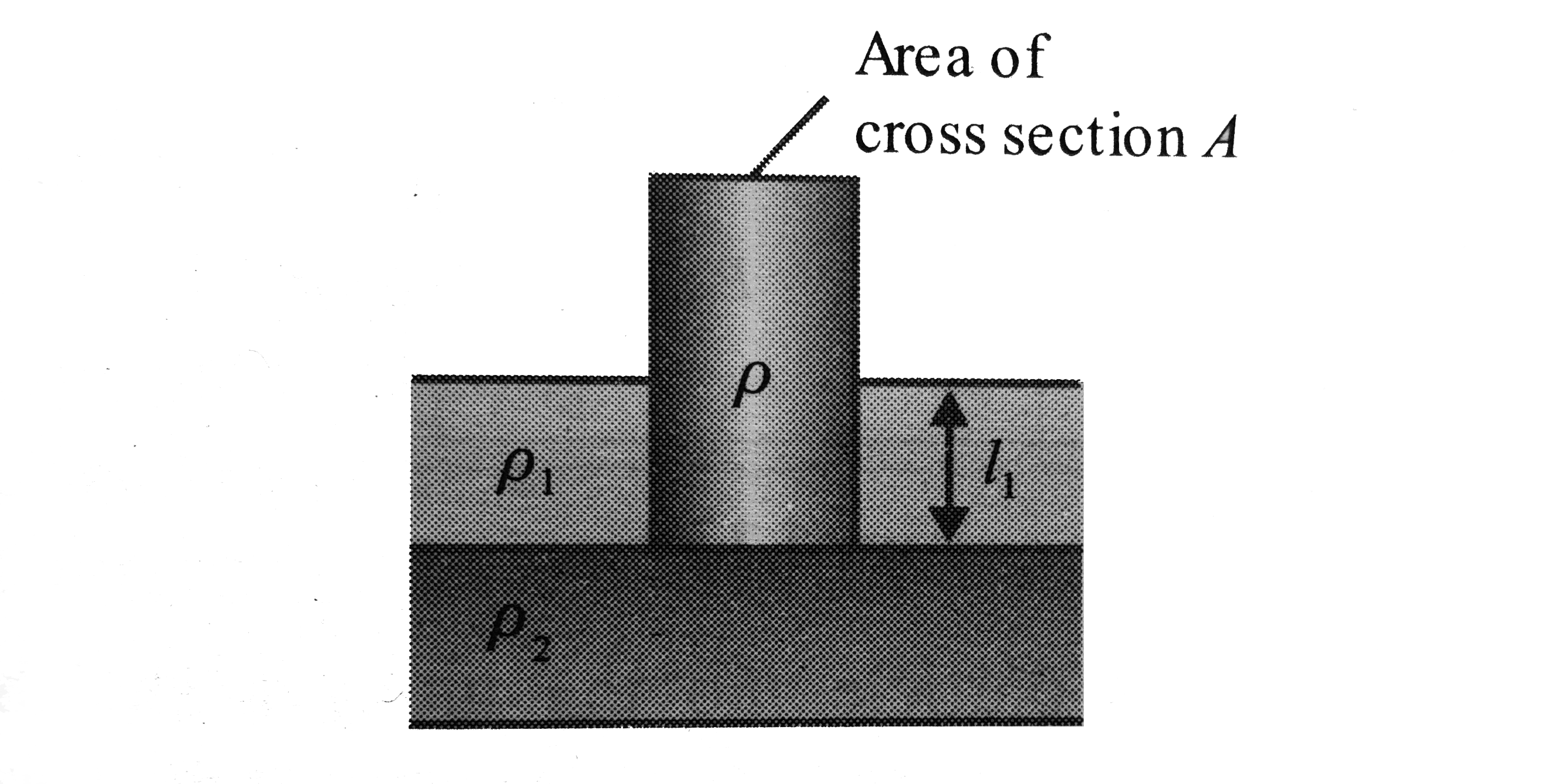
View SolutionA small ball of density 4ρ0 is released from rest just below the surface of a liquid. The density of liquid increases with depth as ρ=ρ0(1+ay) where a=2m−1 is a constant. Find the time period of its oscillation. (Neglect the viscosity effects).
View SolutionIf two liquids of same volume but different densities ρ1 and ρ2 are mixed, then the density of the mixture is:
View SolutionA vertical pole of length l, density ρ, area of cross section A, floats in two immiscible liquids of densities ρ1 and ρ2. In equilibrium position the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, the time period of oscillation is..........
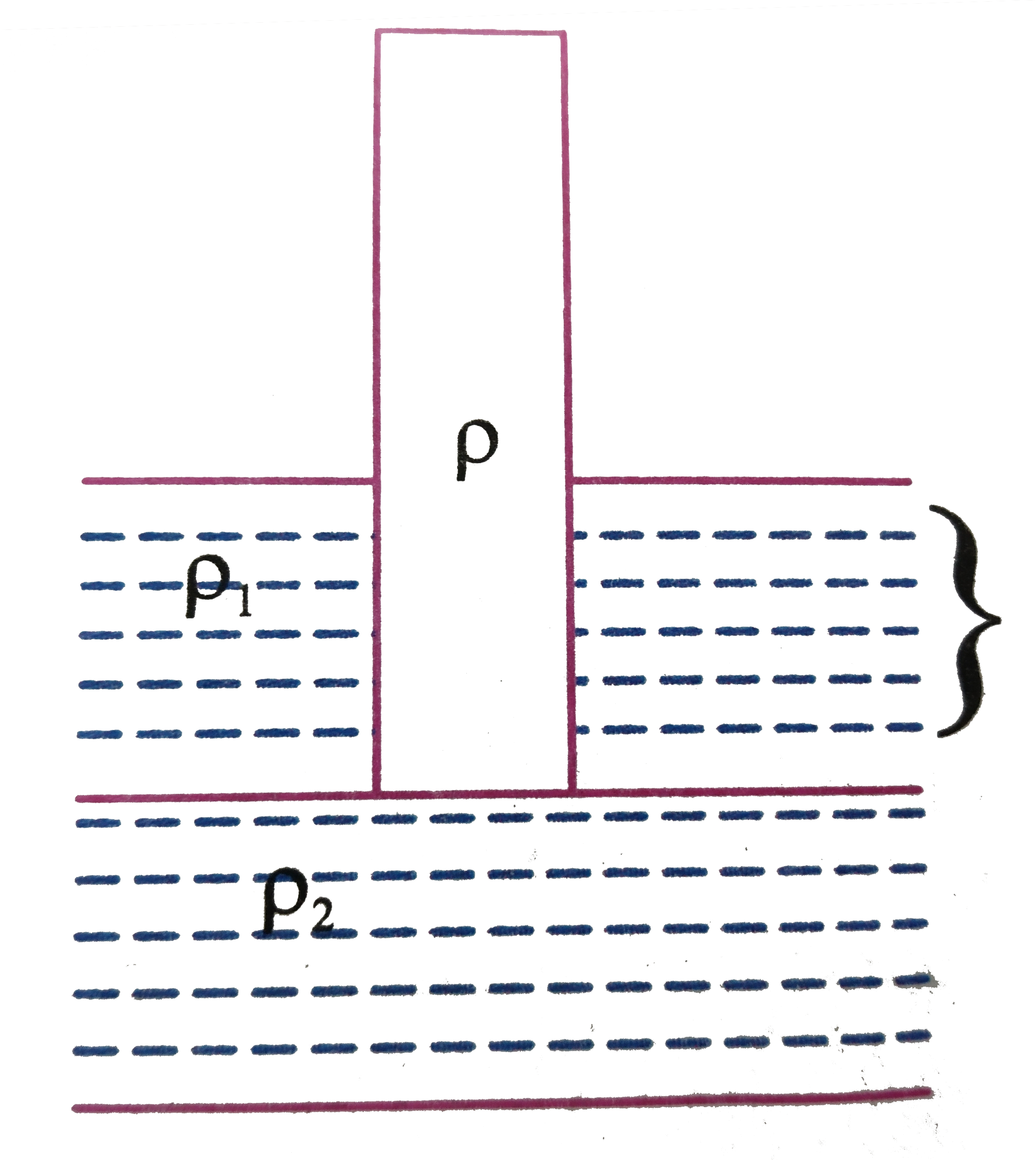
View Solution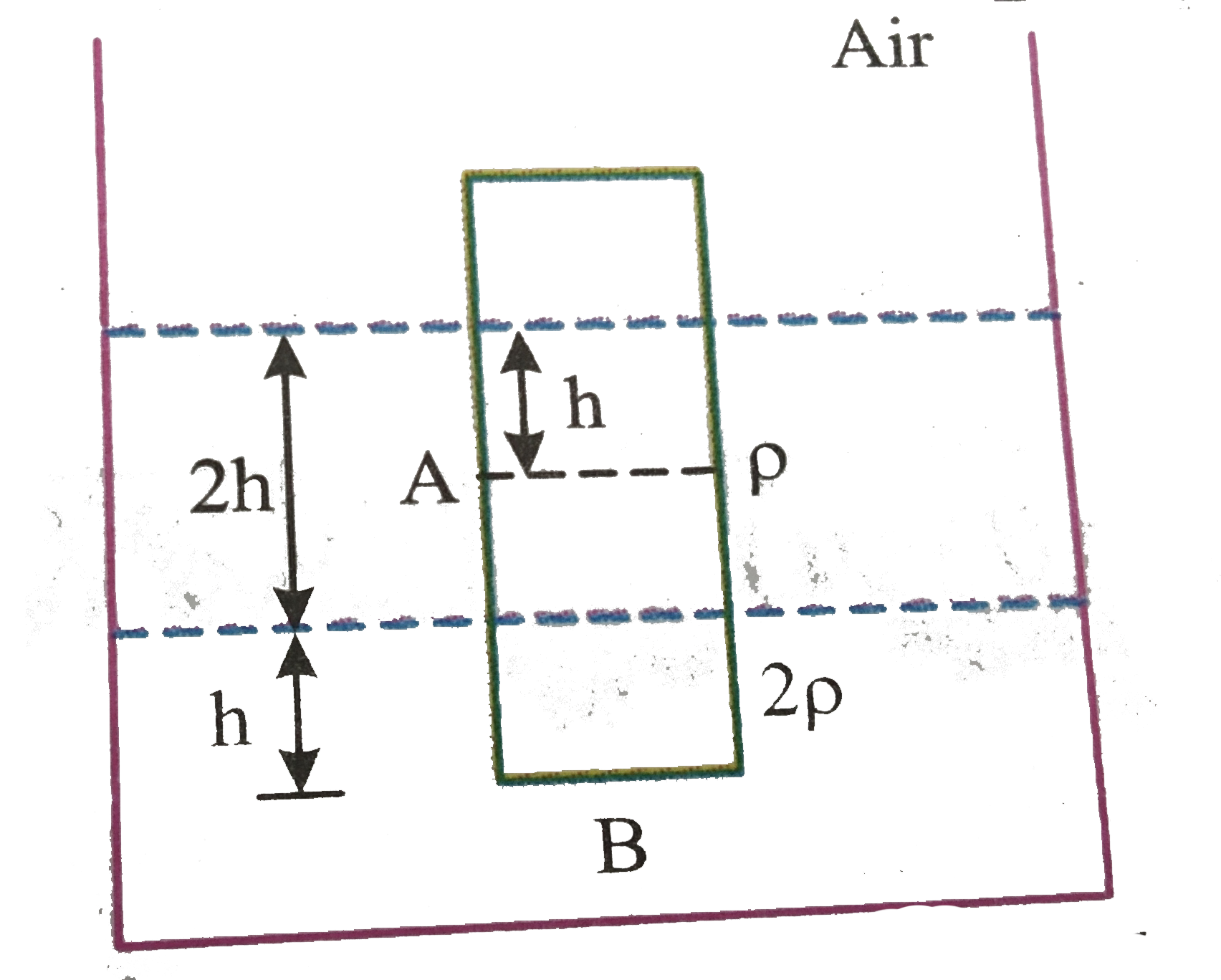
A cylinder stands vertical in two immiscible liquids of densities ρ and 2ρ as shown. Find the difference in pressure at point A and B:
View Solution
