
A spherical ball of radius R is floating at the interface of two liquids with densities ρ and 2ρ. The volumes of the ball immersed in two liquids are equal. Answer the following questions:
Find the force exerted by the liquid with density 2ρ on the ball
πR2ρg(H+2R3)
23πR2ρg
43πR2ρg
2πR2ρg(H+2R3)
The correct Answer is:D
πR22Hρg+23πR32ρg=F
2πR2Hρg+4πR3ρg3=F,2πR2ρg(H+2R3)=F
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Paragraph Type Questions
5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Single Answer Questions
108 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - More Than One Alternative Type Question
32 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
Similar Questions
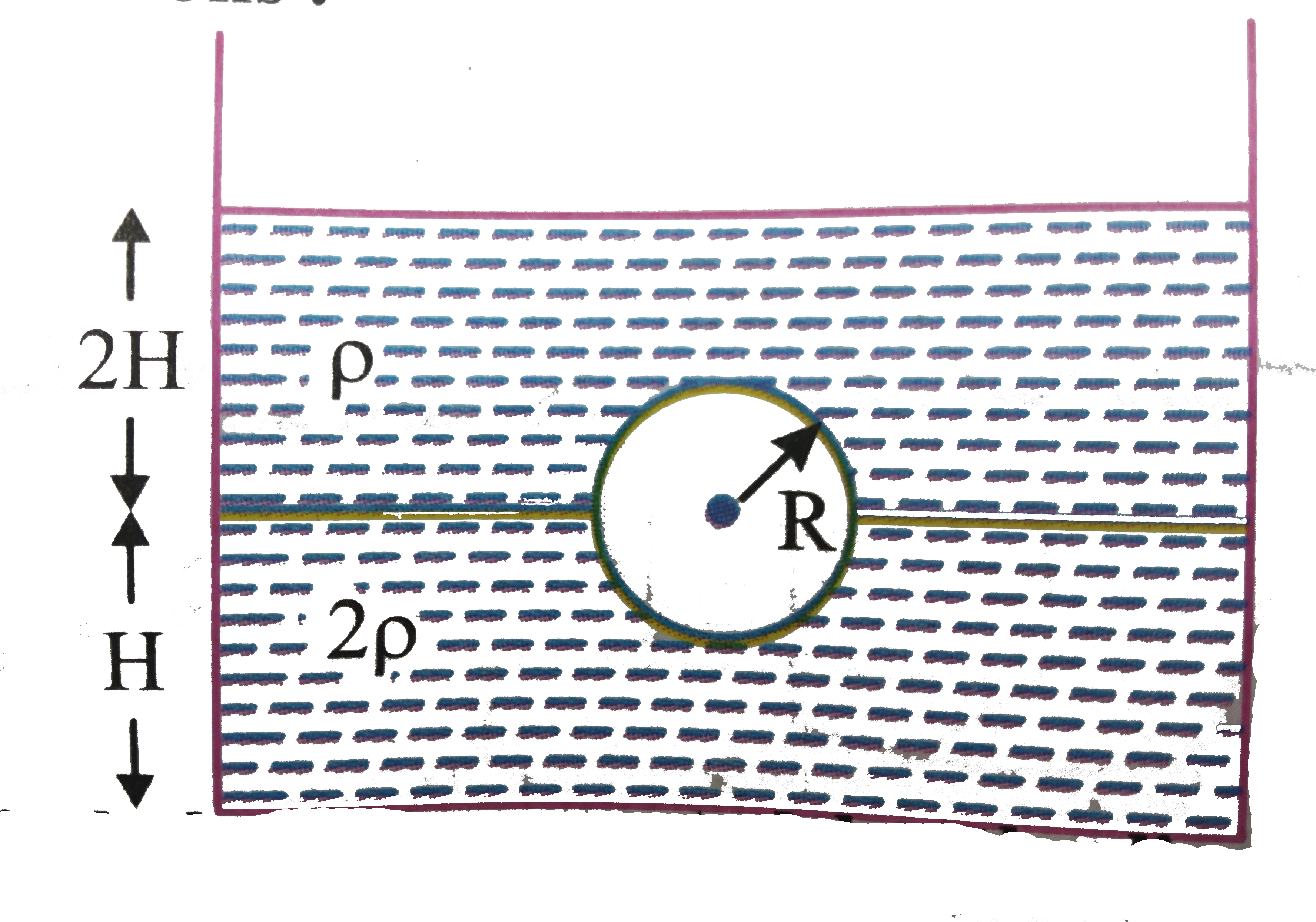
A solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
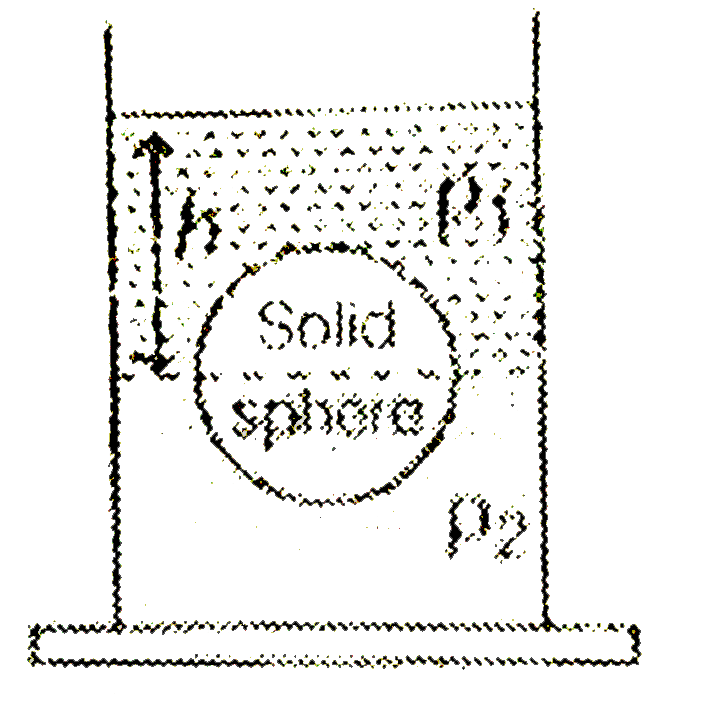
View SolutionA uniform sphere of density ρ floats at the interface of two liquids of densities ρ1 and ρ2(>ρ1) The sphere has 23 rd of vertical diameter in denser liquid and remaining part in the other liquid.If aρ=bρ1+cρ2 then b+c-a=_______.
View Solution
Knowledge Check
A spherical ball of radius R is floating at the interface of two liquids with densities ρ and 2ρ. The volumes of the ball immersed in two liquids are equal. Answer the following questions:
If a hole is drilled at the bottom of the vessel then volume of the ball immersed inliquid with density ρ willAremain sameBdecreaseCincreaseDdecrease first then increaseA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
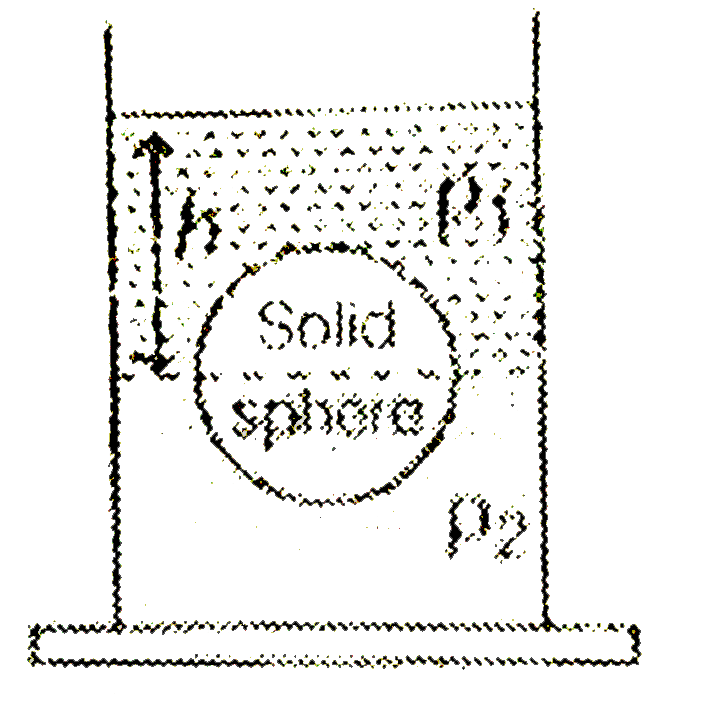 Ap0πr2+(h−23r)πr2ρ1gB(h−23r)πr2ρ1gC23πr2ρ1gDp0×πr2
Ap0πr2+(h−23r)πr2ρ1gB(h−23r)πr2ρ1gC23πr2ρ1gDp0×πr2A uniform cube of mass M is floating on the surface of a liquid with three fourth of its volume immersed in the liquid (density=ρ). The length of the side of the cube is equal to
 A(4M/3ρ)2/3B(M/3ρ)2/3C(M/4ρ)2/3DNone of these
A(4M/3ρ)2/3B(M/3ρ)2/3C(M/4ρ)2/3DNone of these
Two liquids of densities ρ and 3rho having volumes 3V and V are mixed together. Find density of the mixture.
View SolutionA rubber ball of bulk modulus B is taken to a depth h of a liquid of density ρ. Find the fractional change in the radius of the ball.
View SolutionA rubber ball of bulk modulus B is taken to a depth h of a liquid of density ρ. Find the fractional change in the radius of the ball.
View SolutionTwo liquids of densities 2ρ and ρ having their volumes in the ratio 3:2 are mixed together. Density of the mixture will be
View SolutionTwo liquids of densities 2ρ and ρ having their volumes in the ratio 3:2 are mixed together. Density of the mixture will be
View Solution
