A glass capillary tube is of the shape of a truncated cone with an apex angle α so that its two ends have cross sections of different radii. When dipped in water vertically, water rises in it to a high h, where the radius of its cross section is b. If the surface tension of water is S, its density if ρ, and its contact angle with glass is θ, the value of h will be (g is the acceleration due to gravity)
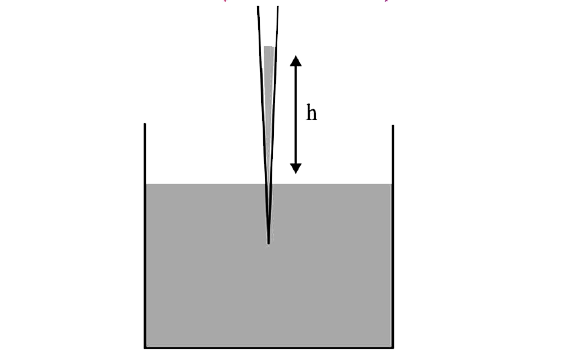
2Sbρgcos(θ−α)
2Sbρgcos(θ+α)
2Sbρgcos(θ−α2)
2Sbρgcos(θ+α2)
The correct Answer is:D
bR=cos(θ+α2)
Using pressure equation along the path MNTK
p0−2SR+hρg=p0
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - integer Type Questions
25 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Level 1 (H.W)
55 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Paragraph Type Questions
5 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
Similar Questions
In a capillary tube , water rises to a height of 4 cm If its cross section area were one forth , the water would have to rises a height of
View SolutionThe surface tension of water is 7×10−2N/m2 and its angle of contact with glass is zero . The rise of water in a capillary tube of diameter 0.5 mm is ………..
View Solution
Knowledge Check
When liquid medicine ρ is to be put in the eye, it is done with the help of a dropper. As the bulb on the top of the dropper is pressed, a drop froms at the opening of the dropper. We wish to estimate the size of the drop. We first assume that the drop formed at the opening is osperical becaus ethat requires a minimum increase in its surface energy. To datermine the size., we calculate the net vertical force due to the surface tension T when the radius of the drop is R. When this force become smaller than the wight of the drop, the drop gets detached from the droppr.
A glass capillary tube is of the shape of a truncated cone with an apex angle α so that its two ends have cross sections of different raddi. When dipped in water verically, water rises in it to a height h, where the radius of its cross section is b. If the surface tension of water is S, its density is ρ, and its contact angle with glass is θ, the value of h will be (g is the acceleration due to gravity)
 A2Sbρgcos(θ−α)B2Sbρgcos(θ+α)C2Sbρgcos(θ−α/2)D2Sbρgcos(θ+α/2)
A2Sbρgcos(θ−α)B2Sbρgcos(θ+α)C2Sbρgcos(θ−α/2)D2Sbρgcos(θ+α/2)Two capillary tubes of different diameters are dipped in water .The rise of water is :
Agrater in the tube of smaller diameterBgreater in the tube of larger diameterCsame in both tubesDnone of theseTwo vertical glass plates 1 mm apart are dipped into water. How high will the water rise between the plates. If the surface tension of water is 70 dyne cm−1
A1.43 cmB1.63 cmC2.86 cmD3.86 cm
Water rises upto a height h in a capillary tube of radius r. What is the network done in this process if the density of water is ρ ?
View SolutionIf a capillary of radius r is dipped in water the height of water that rises in it is h and its mass is M . If the radius of the capillary is doubled the mass of water that rises in the capillary will be
View SolutionWater rises to a height h in a capillary tube of cross-sectional area A. the height to which water will rise in a capillary tube of cross-sectional area 4A will be
View SolutionA capillary tube of area of cross-section A is dipped in water veritcally. Calculate the amount of heat evolved as the water rises in the capillary tunbe upto height h. The density of water is ρ
View SolutionA capillary tube of radius 'r' is immersed in water and water rises in it to a height H. Mass of water in the capillary tube is m. If the Capillary of radius 2r is taken and dipped in water, the mass of water that will rise in the capillary tube will be
View Solution
