The high domes of ancient buildings have structural value (besides beauty). It arises from pressure difference on the 2 faces due to curvature (as in soap bubbles). There is a dome of radius 5 m and uniform (but small ) thickness. The surface tension of its masonry structure is about 500 N/m. Treated as hemispherical, the maximum load that the dome can support is nearest to
1500kg−Wt
3000kg−Wt
6000kg−Wt
12000kg−Wt
The correct Answer is:B
ΔP=4Tr
Maximum load that can be supported by the dome
=(ΔP)πr2=4TR×πR2=4πTR
=4×227×500×5=31400N
≈3000kgWt (nearly)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - integer Type Questions25videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Level 1 (H.W)55videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Paragraph Type Questions5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q13videos
MATHEMATICAL REVIEW & PHYSICAL WORLD
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
Similar Questions
An ancient building has a done of 5m radius and uniform but small thickness. The surface tension of its masionary structure is about 500Nm−1 . Treated as hemisphere, find the maximum load that dome can support.
View SolutionA narrow capillary tube is dipped 10cm below water surface and a liquid bubble of radius 2mm formed at the lower end by blowing air through the tube.
a. Calculate the excess pressure due to surface tension.
b. What is the pressure required in the tube in order to blow a hemispherical bubble at its end in water?
The surface tension of water at temperature of the experiment is 7.30×10−2N/m. 1 atmospheric pressure =105Pa, density of water =1000kg/m3View Solution
Knowledge Check
- Question 1 - Select One
Supernova refer to the explosion of a massive star. The material in the central case of such a star continues to collapse under its own gravitational pull. If mass of the core is less is than 1.4 times the mass of sun, its collapse finally results in a white dwarf star. However, if the core has a mass greater than this, it could end up soon as a neutron. star and if its mass is more than about three solar masses, the collapse may still continue till the star becomes a very small object with an extremely high value of density called a 'Black hole'. Escape speed for a black hole is very large. The figure shows a block hole of radius R and another concentric sphere of radius RS, called the 'Schwarzschild Radius'. It is the critical radius at which escape speed equals the speed of light c. Nothing even the light, can escape from within the sphere of Radius RS. So light from a black hole can not escape and hence the terminology 'black hole'. There has been astronomical evidence of a small and massive object at the centre of our galaxy the 'Milky way'. Suppose that there is a particle at a distance about 6 light years. that orbits this massive object with an orbital speed of about 2×105m/s. Use the given data whereever necessary and answer the questions that hollow. G=6.67×10−11N−m2/kg2, Solar mass M=2×1030kg,C=3×108m/s,1 light year =9.5×1015m.
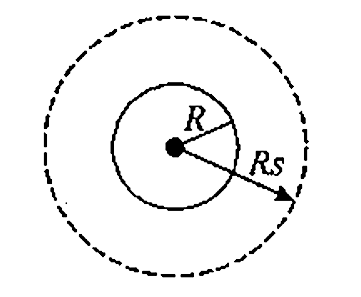
If mass of earth ME≈6×1024kg and its radius RE=6400km, to what fraction of its presents radius does the earth need to be compressed in order to become a black hole ?
(Give only the order of your answer)A10−4B10−9C10−7D10−14 - Question 2 - Select One
Supernova refer to the explosion of a massive star. The material in the central case of such a star continues to collapse under its own gravitational pull. If mass of the core is less is than 1.4 times the mass of sun, its collapse finally results in a white dwarf star. However, if the core has a mass greater than this, it could end up soon as a neutron. star and if its mass is more than about three solar masses, the collapse may still continue till the star becomes a very small object with an extremely high value of density called a 'Black hole'. Escape speed for a black hole is very large. The figure shows a block hole of radius R and another concentric sphere of radius RS, called the 'Schwarzschild Radius'. It is the critical radius at which escape speed equals the speed of light c. Nothing even the light, can escape from within the sphere of Radius RS. So light from a black hole can not escape and hence the terminology 'black hole'. There has been astronomical evidence of a small and massive object at the centre of our galaxy the 'Milky way'. Suppose that there is a particle at a distance about 6 light years. that orbits this massive object with an orbital speed of about 2×105m/s. Use the given data whereever necessary and answer the questions that hollow. G=6.67×10−11N−m2/kg2, Solar mass M=2×1030kg,C=3×108m/s,1 light year =9.5×1015m.
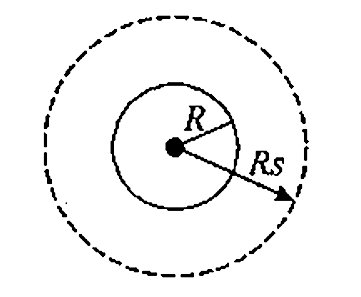
Theories suggest that it is not possible for a single star to have a mass of more than 50 masses. The massive object at the centre of milky way galaxy is most likely to be a :Awhite dwarfBneutron starCblack holeDsingle ordinary star - Question 3 - Select One
Supernova refer to the explosion of a massive star. The material in the central case of such a star continues to collapse under its own gravitational pull. If mass of the core is less is than 1.4 times the mass of sun, its collapse finally results in a white dwarf star. However, if the core has a mass greater than this, it could end up soon as a neutron. star and if its mass is more than about three solar masses, the collapse may still continue till the star becomes a very small object with an extremely high value of density called a 'Black hole'. Escape speed for a black hole is very large. The figure shows a block hole of radius R and another concentric sphere of radius RS, called the 'Schwarzschild Radius'. It is the critical radius at which escape speed equals the speed of light c. Nothing even the light, can escape from within the sphere of Radius RS. So light from a black hole can not escape and hence the terminology 'black hole'. There has been astronomical evidence of a small and massive object at the centre of our galaxy the 'Milky way'. Suppose that there is a particle at a distance about 6 light years. that orbits this massive object with an orbital speed of about 2×105m/s. Use the given data whereever necessary and answer the questions that hollow. G=6.67×10−11N−m2/kg2, Solar mass M=2×1030kg,C=3×108m/s,1 light year =9.5×1015m.
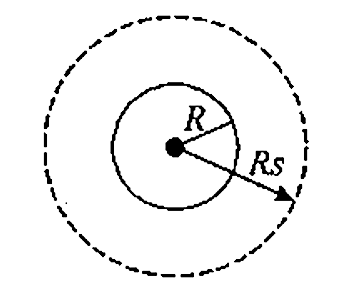
Mass (in kg) of the massive object at the centre of the milky galaxy is of the order :A1032B1037C1043D1029
A spaceship is orbiting the earth in a circular orbit at a height equal to radius of the earth (Rc=6400km) from the surface of the earth. An astronaut is on a space walk outside the spaceship. He is at a distance of l = 200 m from the ship and is connected to it with a simple cable which can sustain a maximum tension of10 N. Assume that the centre of the earth, the spaceship and the astronaut are in a line. Mass of astronaut along with all his accessories is 100 kg. Do you think that a weak cable that can only take a load of 10 N, can prevent him from drifting in space ? Make a guess. Estimate the tension in the cable. [Acceleration due to gravity on the surface of[Earth=9.8m/s2]
View SolutionA thin rod of mass M and length a is free to rotate in horizontal plane about a fixed vertical axis passing through point O. A thin circular disc of mass M and of radius a/4 is pivoted on this rod with its center at a distance a/4 from the free end so that it can rotate freely about its vertical axis. Assume that both rod and disc have uniform density and they remain horizontal during motion. An outside stationary observer finds the rod rotating with an angular velocity Ω and the disc rotating about its vertical axis with angular velocity 4Ω. Total angular momentum of system about point O is (Ma2Ω48)n. The value of n is
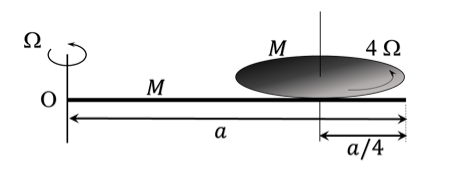 View Solution
View SolutionEarly crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii. Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller cation fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
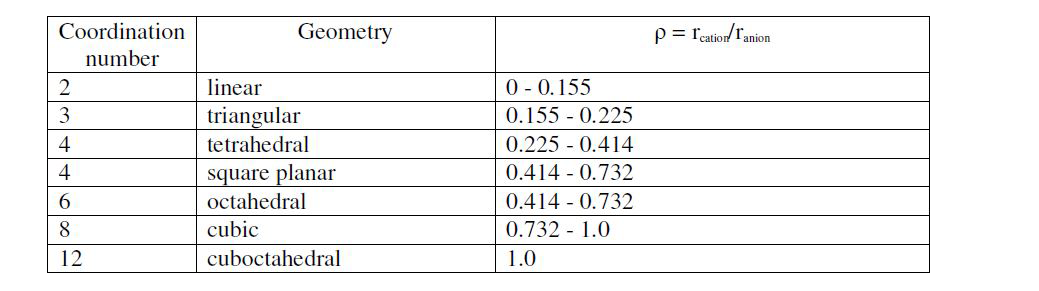
A solid AB has square planar structure. If the radius of cation A+ is 120pm,Calculate the maximum possible value of anion B−View SolutionEarly crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii.
Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller catin fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
Coordiantion numberGeometryρ=rcationramion2linear0−0.1553triangular0.155−0.2254tetrahedral0.225−0.4144square planar0.414−0.7326octahedral0.414−0.7328cubic0.732−1.012cuboctahedral1.0
(Source : Ionic Radii and Radius Ratios. (2021, June 8). Retrieved June 29, 2021, from https://chem.ibretexts.org/@go/page/183346)
A solid AB has square planar structure. If the radius of cation A+ is 120 pm, calculate the maximum possible value of anion B−.View SolutionTwo independent light sources are always incoherent. This is because phase of light emitted is random and phase difference, at any point, changes very rapidly with time. So as to obtain observable interference, we require coherent sources which emit light of same wavelength such that phase difference at any point does not change with time. In different interference experiments, the method to obtain two coherent sources could be different. In Fresnel's biprism experiment, two virtual images of a real source, which are formed due to refraction at the biprism, act as coherent source. In Lloyd’s mirror experiment, a real source and its virtual image formed due to reflection at a plane mirror act as coherent source. Two images of a source or a source and its image are coherent because of their phase correlation. It is also possible to obtain coherent sources by forming two images of a point source in the following manner.As shown in the figure, S is a monochromatic point source. A thin circular lens is cut into two identical halves L, and L2 by a plane passing through a diameter. L1 is kept above the axis and L2 below it is in a symmetrical manner such that the gap between the two is 0.1 mm. Each forms an image Qf the source and the two images, say, Si and S2 , act as coherent sources. Superposition of waves from these coherent sources will result in observable interference and a pattern can be obtained on a screen.The lens which has been cut to from L, and L2 is made of a material of refractive index 1.5 for the wavelength emitted by the source S. Radius of curvature of each surface of the lens is 18 cm. Source S is 30 cm along the axis fro Li and L2 . It is found that smallest distance from O along the screen at which intensity is half of the maximum intensity is 0.1 mm. It is also observed that the highest order of maximum intensity in the interference patter is 416.
Q Phase difference between the light waves 0.1 mm from along the screen, where intensity is half the maximum value, is
 View Solution
View Solution

