The temperature of the two ends A and B of a rod of length 25cm and circular cross section are 100∘C and 0∘C respectively In the steady state, find the temperature at a point 10cm from the end B (ifnore loss of heat from curved surface of the body) ?
To find the temperature at a point 10 cm from the end B of a rod that has one end at 100°C and the other at 0°C, we can use the concept of linear temperature distribution in a steady state. Here’s how we can solve the problem step by step:
Step 1: Understand the Setup
We have a rod of length L=25cm with:
- Temperature at end A (0 cm) = TA=100∘C
- Temperature at end B (25 cm) = TB=0∘C
We need to find the temperature at a point X=10cm from end B.
Step 2: Determine the Position from End A
Since we are measuring from end B, we can calculate the position from end A:
- Distance from A to the point X is 25cm−10cm=15cm.
Step 3: Use the Linear Temperature Gradient
In a steady state, the temperature gradient is linear. The formula for temperature at a distance x from one end of the rod is given by:
T(x)=TA+(TB−TAL)⋅x
Step 4: Substitute the Values
Here, TA=100∘C, TB=0∘C, L=25cm, and x=15cm:
T(15)=100+(0−10025)⋅15
Step 5: Calculate the Temperature
Now, calculate the temperature:
T(15)=100+(−4)⋅15
T(15)=100−60=40∘C
Final Answer
Thus, the temperature at the point 10 cm from end B is 40∘C.
---
We have a rod of length L=25cm with:
- Temperature at end A (0 cm) = TA=100∘C
- Temperature at end B (25 cm) = TB=0∘C
Since we are measuring from end B, we can calculate the position from end A:
- Distance from A to the point X is 25cm−10cm=15cm.
In a steady state, the temperature gradient is linear. The formula for temperature at a distance x from one end of the rod is given by:
T(x)=TA+(TB−TAL)⋅x
Here, TA=100∘C, TB=0∘C, L=25cm, and x=15cm:
T(15)=100+(0−10025)⋅15
Now, calculate the temperature:
T(15)=100+(−4)⋅15
T(15)=100−60=40∘C
Thus, the temperature at the point 10 cm from end B is 40∘C.
Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - C .U .Q
89 Videos
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL -1 (C.W)
1 Videos
- THERMODYNAMICSBOOK - NARAYNACHAPTER - THERMODYNAMICSEXERCISE - Exercise
187 Videos
- UNITS AND MEASUREMENTSBOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - STATEMENT TYPE QUESTION
23 Videos
Similar Questions
The lleft end of a copper rod (≤n>h=20cm.Areaofcrosssection=0.02cm2 is maintained at 20∘C and the right end is maintained at 80∘C . Neglecting any lkkoss of heat through radiation, find (a) the temperature at a point 11cm from the left end and (b) the heat current through the rod. thermal conductivity of copper =385Wm=−1^(@)C^(-1) .
View SolutionIn a steady state of thermal conduction, temperature of the ends A and B of a 20 cm long rod are 100∘C and 0∘C respectively. What will be the temperature of the rod at a point at a distance of 6 cm from the end A of the rod
View Solution
Knowledge Check
Two ends of a conducting rod of varying cross-section are maintained at 200∘Cand0∘C respectively. In steady state :
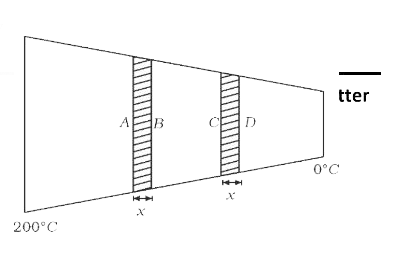 Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Atemperature differences across AB and CD are equalBtemperature difference across AB is greater than that across CDCtemperature difference across AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.Two ends of a conducting rod of varying cross-section are maintained at 200∘C and 0∘C respectively. In steady state:
 Atemperature differences across ABandCD are equalBtemperature difference aross AB is greater than that across CDCtemperature difference aross AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.
Atemperature differences across ABandCD are equalBtemperature difference aross AB is greater than that across CDCtemperature difference aross AB is less than that across CDDtemperature difference may be equal or different depending upon thermal conductivity of the rod.The temperature of hot and cold end of a 20 cm long rod in thermal steady state are at 100∘C and 20∘C respectively. Temperature at the centre of the rod is
A50∘CB60∘CC40∘CD30∘C
Two rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature (θ) of the interface will be -
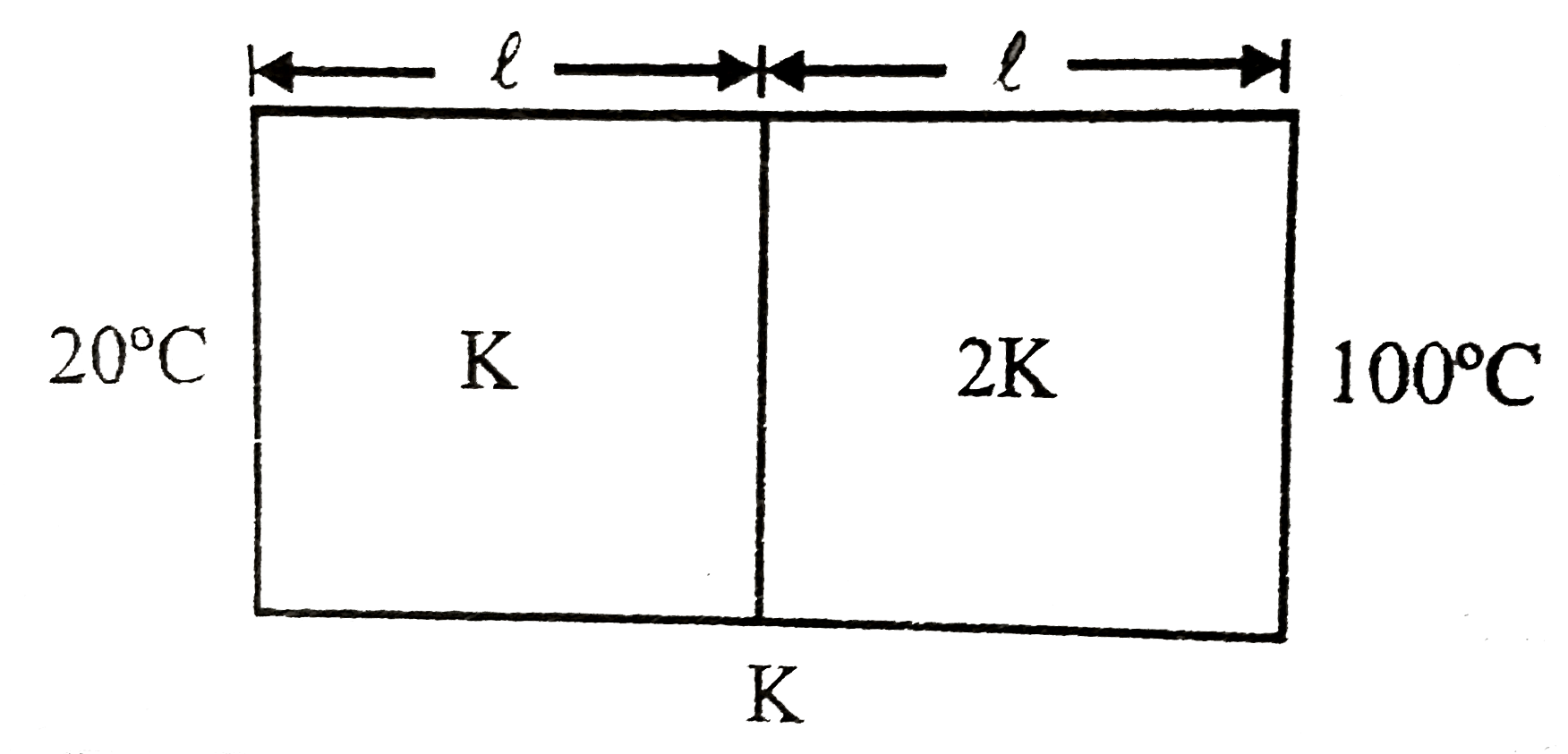
View SolutionTemperature of hot end and cold end of a rod, which is in steady state are 100∘C and 40∘C respectively. The area of cross section of rod and its thermal conductivity are uniform. The temperature of rod at its mid point is (Assume no heat loss thorugh lateral surface)
View SolutionIn a steady state of heat conduction the temperature of the ends A and B of a rod 100cm long per 0∘C and 100∘C The temperature of the rod at a point 60cm distant from the end A is .
View SolutionThe end A of rod AB of length 1 m is maintained at 80∘C and the end B at 0∘C. The temperature at a distance of 60 cm from the end A is
View SolutionAssume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. Three metal rods made of copper, aluminium and brass are each 15 cm long and 2 cm in diameter. These rods are placed end to end, with aluminium between the other two. The free ends of the copper and brass rods are maintained at 100∘C and 0∘C respectively. The system is allowed to reach the steady state condition. Assume there is no loss of heat anywhere.
Under steady state condition the equilibrium temperature of the copper aluminium junction will be
View Solution
