Three rods of lengths L,21 and 3L having thermal conductivities 3K,2K and K are connected end to end If cross sectional areas of three rods are equal If cross sectional areas of three rods are equal then equivalent thermal conductivity of the system is .
18K/13
36K/133
9K/13
12K/13
The correct Answer is:A
Reff=R1+R2+R3
l1+l2+l3Keff=l1K1+l2K2+l3K3 .
Topper's Solved these Questions
Similar Questions
" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionThree rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is
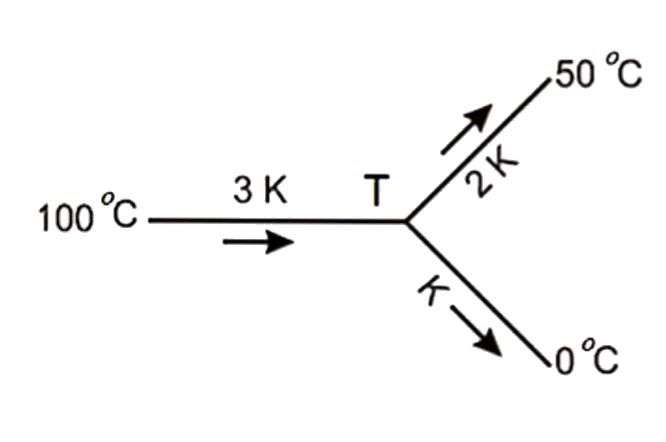
View Solution
Knowledge Check
Two rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
A(5/6)KB1.5KC1.2KD(8/9)KA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLThree rods of same dimensions have thermal condutivity 3K,2K and K They are arranged as shown in Then the temperature of the junction in steady state is
 .A2003∘CB1003∘CC75∘CD81∘C
.A2003∘CB1003∘CC75∘CD81∘C
Find the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1 . Thermal conductivity of the material of the rod is K.

View SolutionTwo rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
View SolutionTwo rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
View SolutionThree rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is

View SolutionTwo rods of length d1 and d2 and coefficients of thermal conductivites K1 and K2 are kept touching each other. Both have the same area of cross-section. The equivalent thermal conductivity.
View Solution
