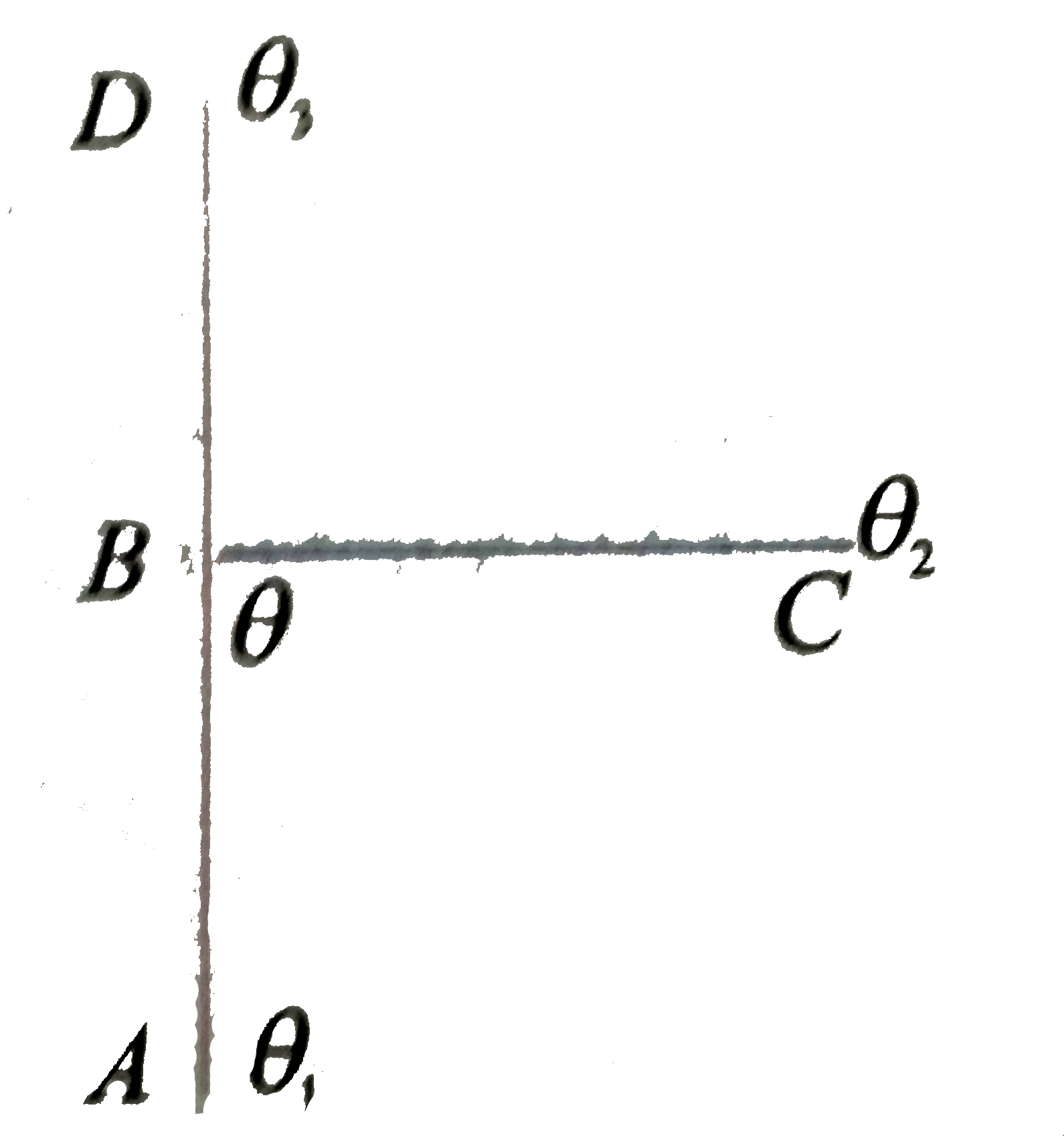
Three rods AB,BCand BD having thremal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in The ends A,C and D are at temperature θ1,θ2 and θ3 respectively Find the temperature of the junction B
(Assume steady state and θ1>θ>θ2>θ3)
 .
.
Let the thermal conductivities of the rods AB,BC and BD be K,2K and 3K respectively and their lenths be 2L,L and L we have
[ΔQΔt]AB=[ΔQΔt]BC+[ΔQΔt]BD
i.eKA(θ1−θ)2L=2KA(θ−θ2)L+3KA(θ−θ3)L
∴θ=111(θ1+4θ2+6θ3) .
Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - C .U .Q
89 Videos
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL -1 (C.W)
1 Videos
- THERMODYNAMICSBOOK - NARAYNACHAPTER - THERMODYNAMICSEXERCISE - Exercise
187 Videos
- UNITS AND MEASUREMENTSBOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - STATEMENT TYPE QUESTION
23 Videos
Similar Questions
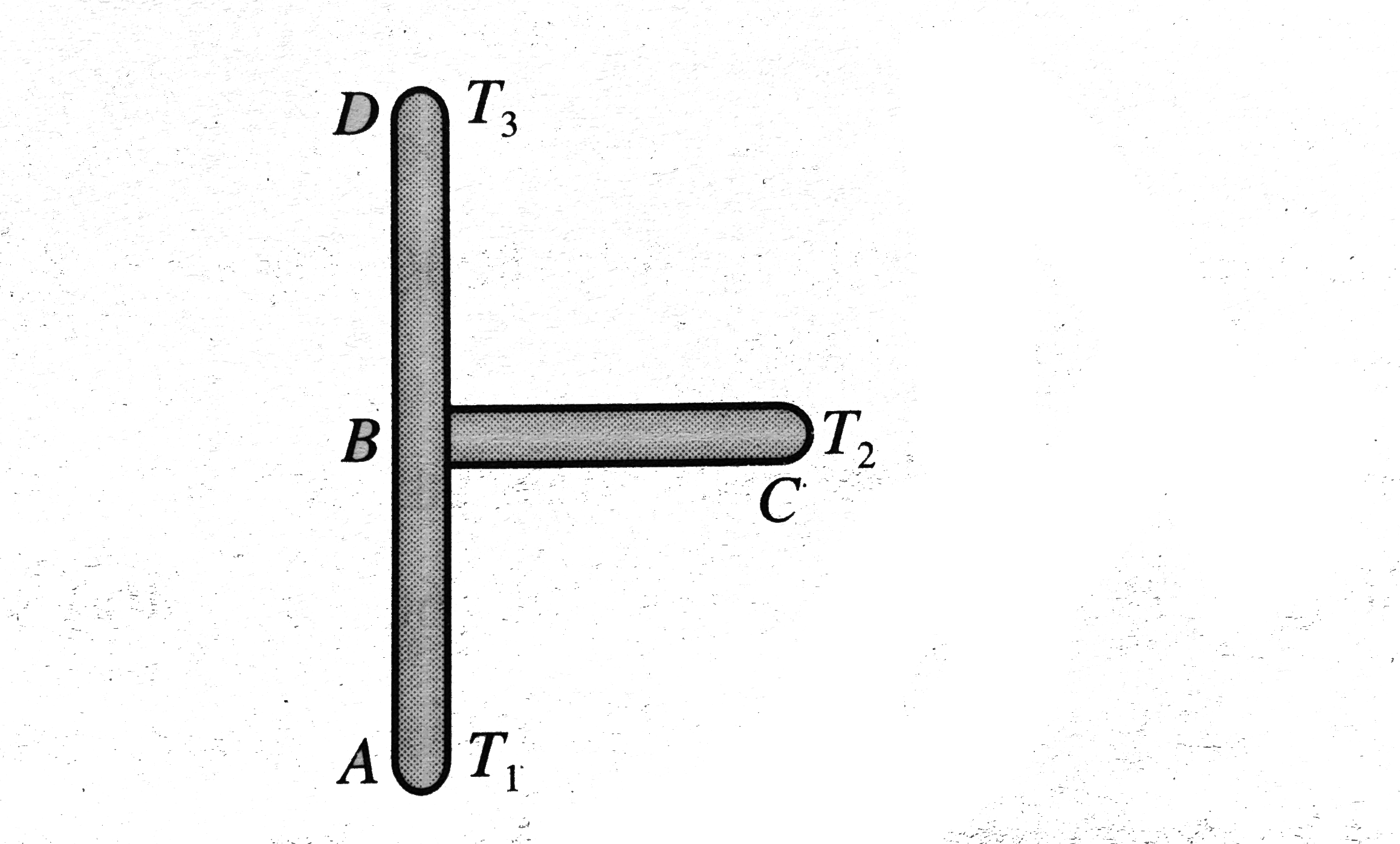
Three rods AB, BC and BD having thermal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in Fig. The ends A, C and D are at temperature T1,T2 and T3 respectively Find the temperature of the junction B. Assume steady state.
View SolutionTwo slabs are placed adjacently having thermal resistance R1&R2, their free ends maintained at temperature of θ1, & and θ2, respectively. Find the temperature of junction.

View Solution
Knowledge Check
Three identical solid spheres (1, 2 and 3) are allowed to roll down from three inclined plane of angles θ1,θ2andθ3 respectively starting at time t = 0, where θ1>θ2>θ3, then
Asphere 1 will reach the bottom firstBsphere 2 will reach the bottom firstCsphere 3 will reach the bottom firstDall the spheres will reach the bottom at the same timeA thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
AL0[1+α(θ1+θ2)]BL0(1+α(θ1+θ22))CL0(1+αθ1)DL0(1+α(θ1+θ22))_2019_CBT4_E01_064_Q01.png)
Two conductors of same cross-section and conductivities K, 3K and length 3 d and d respectively are connected end to end as shown in figure. Temperature of end of first conductor is θ1 and that of second conductor is θ2 .the temperature of junction is steady state is (θ2>θ1)A10θ2+9θ119Bθ2+9θ10C9θ2+θ110D9θ2+10θ119
Find the equation of line joining the points : (acosθ1,bcosθ2),(acosθ2,bsinθ2)
View SolutionIf sinθ1+sinθ2+sinθ3, then find the value of cosθ1+cosθ2+cosθ3.
View SolutionLet 0<θ1<θ2<θ3< denote the positive solution of the equation 3+3cosθ=2sin2θ. The value of θ3+θ7 is 3 (b) 4 (c) 5 (d) 6
View SolutionThe ends of a metal rod are kept at temperature θ1andθ2 with θ2>θ1. At steady state the rate of flow of heat along the rod is directly proportional to
View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View Solution
