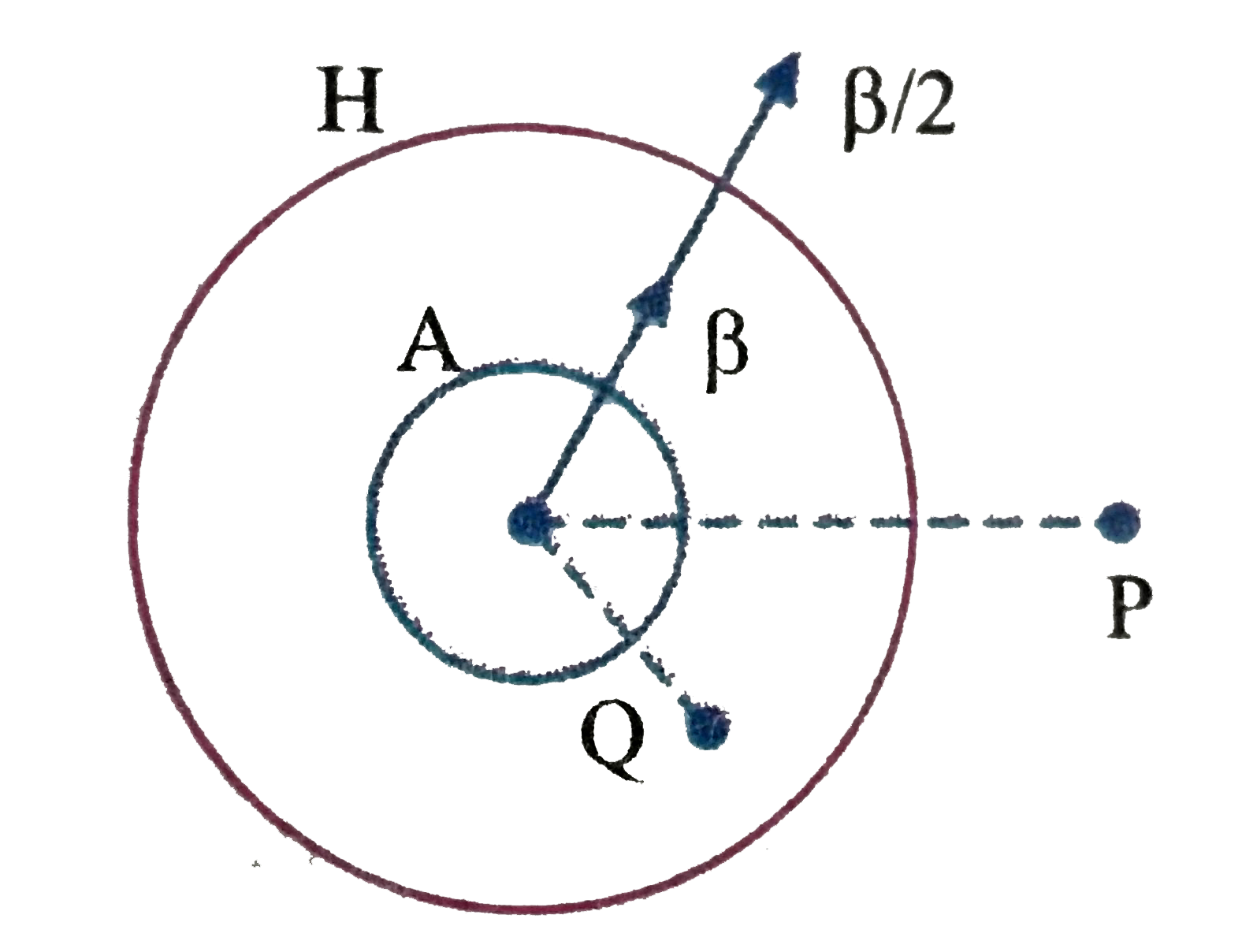
Consider a spherical body A of radius R which is placed concentrically in a hollow enclosure H of radius 4R as shown in the The temperature of the body A and H are TA and TH respectively Emissivity transmittivity and reflactivity of two bodies A and H are (ea,eH),?(tA,tH), and (rA,rH) respectively (Assume no absorption of the thermal energy by the space in between the body and enclosure as well as outside the enclousre and all radiations to be emitted and absorbed normal to the surface [Tskeσ×4πr2×3004=βJ/s]
![Consider a spherical body A of radius R which is placed concentrically in a hollow enclosure H of radius 4R as shown in the The temperature of the body A and H are T(A) and T(H) respectively Emissivity transmittivity and reflactivity of two bodies A and H are (e(a),e(H)),?(t(A),t(H)), and (r(A),r(H)) respectively (Assume no absorption of the thermal energy by the space in between the body and enclosure as well as outside the enclousre and all radiations to be emitted and absorbed normal to the surface [Tske sigma xx 4pi r^(2) xx 300^(4) = betaJ//s] Consider two cases, first one in which A is a perfect black body and the second in which A is a non-black In both the cases temperature of boby A is same equal to 300K and H is at temperature 600K For H t = and a ne 1 For this situation mark out the correct statements (s) .](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NAR_PHY_XI_V05_C02_E01_221_Q01.png)
Consider two cases, first one in which A is a perfect black body and the second in which A is a non-black In both the cases temperature of boby A is same equal to 300K and H is at temperature 600K For Ht=anda≠1 For this situation mark out the correct statements (s) .
The bodies lose their distinctiveness inside the enclosure and both of them emit the same radiation as that of the black body .
The rate of heat loss by A in both cases is the same and is equal βJ/s .
The rate of heat loss by A in both cases are different .
From this information we can calculate exact rate of heat loss by A in different cases .
The correct Answer is:C
The diagram shows the situation clearly The rate at which energy is emitted by A is BηJ/s while crossing the enclousure the rate at which energy is transmitted out is β2
So rate at which A loses energy is βJ/s and the rate at which P and Q receive energy are β/2J/s and βJ/s respectively This energy is received on the area of sphere passing through P and Q Now in this case each of incidence, refleaction absorption take place The rate at which energy has been lost by A is
P=−[P|or|bed−Pemied]
=−[β8+β32+...]+[β2+β8+β32+....]=β2
The rate a which energy is received by P is P1=0 The rate at which energy is receivedly Q is
P2=[β2+β8+...]+[β2+β8+β32+.....]=β2
=β2×43+β4×43=β
Ifβ=σ4πR2×3004 then
σ×4π(4R)2×6004=256β=γ
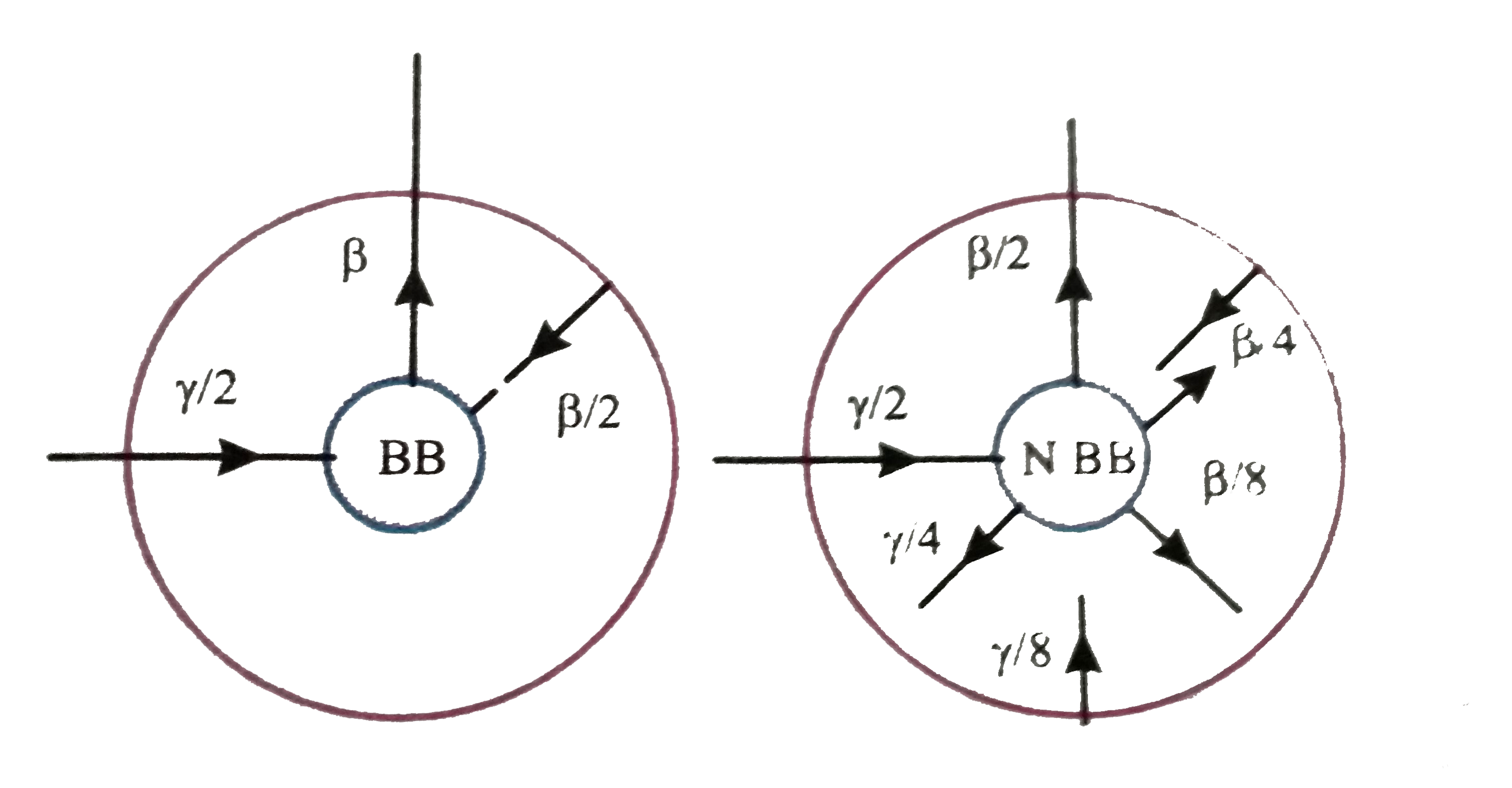
Let aH=eH=0.5 and for A in 2nd case
eA=aA=0.5
For 1st case, Pemitted=βJ/sPabsorbed=γ2+β2
rate at which energy is lost
P=(β−γ2−β2)J/s
For 2nd case Pemitted=(β2+β8+β32)J/s
For 2nd case
Pemitted=(β2+β8+β32+....)+(γ4+γ16+....)=2β3+γ3
Pabsorbed=(β2+β32+...)+(γ4+γ16+....)=β6+γ3
Rate at which heat is lost P=β2 In these questions thermal equilibrium is not acheived and infinite no of reflection absorption can take place before thermal equilibrium has been actived and it is because of very large speed of radiation

Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL-I(H.W)
19 Videos
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL-II(C.W)
27 Videos
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - SINGLE ANSWER QUESTIONS Passage -1
1 Videos
- THERMODYNAMICSBOOK - NARAYNACHAPTER - THERMODYNAMICSEXERCISE - Exercise
187 Videos
- UNITS AND MEASUREMENTSBOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - STATEMENT TYPE QUESTION
23 Videos
Similar Questions
Two spherical black bodies of radii R1 and R2 and with surface temperature T1 and T2 respectively radiate the same power. R1/R2 must be equal to
View SolutionA spherical black body of radius r radiated power P at temperature T when placed in surroundings at temprature T0(<<T) If R is the rate of colling .
View Solution
Knowledge Check
Consider a spherical body A of radius R which is placed concentrically in a hollow enclosure H of radius 4R as shown in the The temperature of the body A and H are TA and TH respectively Emissivity transmittivity and reflactivity of two bodies A and H are (ea,eH),?(tA,tH), and (rA,rH) respectively (Assume no absorption of the thermal energy by the space in between the body and enclosure as well as outside the enclousre and all radiations to be emitted and absorbed normal to the surface [Tskeσ×4πr2×3004=βJ/s]

In above quations if body A has then mark out the correct statements (s) .AThe rate at which A loses the energy is βJ/s .BThe rate at which the spherical surface containing P receives the energy is zeroCThe rate at which the spherical surface containing P receives the energy is βDAll of theseConsider a spherical body A of radius R which is placed concentrically in a hollow enclosure H of radius 4R as shown in the The temperature of the body A and H are TA and TH respectively Emissivity transmittivity and reflactivity of two bodies A and H are (ea,eH),?(tA,tH), and (rA,rH) respectively (Assume no absorption of the thermal energy by the space in between the body and enclosure as well as outside the enclousre and all radiations to be emitted and absorbed normal to the surface [Tskeσ×4πr2×3004=βJ/s]

In the previous question if the enclosure is considered as perfect black body and is maintaind at same temperature as that of temperature of body A then in the two cases .Athe body A emits radiation at the same areBthe body A emits radiation at different ratesCthe temperature of body A remains constant .DNone of theseConsider a spherical body A of radius R which is placed concentrically in a hollow enclosure H of radius 4R as shown in the The temperature of the body A and H are TA and TH respectively Emissivity transmittivity and reflactivity of two bodies A and H are (ea,eH),?(tA,tH), and (rA,rH) respectively (Assume no absorption of the thermal energy by the space in between the body and enclosure as well as outside the enclousre and all radiations to be emitted and absorbed normal to the surface [Tskeσ×4πr2×3004=βJ/s]

The twemperature of H is TH=0K For H take eH=0.5 and tH=0.5 For this situation mark out the correct statements (s) .AThe rate at which A loses the energy is βJ/s .BThe rate at which sperical surface containing P rectives the energy is β2J/s .CThe rate at which sperical surface containing Q receives the energy is βJ/s .DAll of the above
Two spherical black bodies of radii R1 and R2 and with surface temperature T1 and T2 respectively radiate the same power. R1/R2 must be equal to
View SolutionThe heights of two antennas above the earth are hT and hR respectively. The maximum line of sight distancedMbetween the two antennas is (R→Radius of earth)
View SolutionTwo spherical black bodies A and B,having radii rA and rB=2rA emit radiation with peak intensities at wavelength 400 nm and 800 nm respectively. If their temperature are TA and TB respectively in Kelvin scale, their emissive powers are EA and EB then :
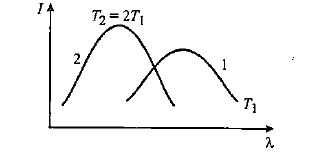
View SolutionThe plots of intensity vs wavelength for two black bodies at temperature T1 and T2 such that T2=2T1, respectively are as shown. Let the energy radiated per second by body I and body 2 be E1 and E2 respectively. Pick up the correct statement(s).
View SolutionA spherical solid blakc body of radius 'r' radiates power 'H' and its rate of cooling is 'C'. If density is constant then which of the following is/are true.
View Solution
