A hot body placed in air is cooled down according to newton's law of cooling the rate of decrease of temperature being k times the temperature difference from the surrounnding Starting from t=0 The time in which the body will lose half of the maximum heat is xLn22k Find the value of x .
The correct Answer is:2
We have −dTdt=k(T−T0)
where T0 is the temperature of the surrounding If T1 is the initial temperature and T is the temperature at any time t then T∫T1dT(T−T0)=−kt0∫0dt
or|in(T−T0)|TT=−k→rIn[T−T0T1−T0]=−kt
or T=T0+(T1−T0)e−kt
The body continues to lose heat till its temperature becomes equal to that of the surrounding The loss of heat Q=mc(T1−T0)
If the body lose half of the maximum loss that it can then decrease in temp Q2=mc(T1−T02)
If body loses this heat in time t then its temperature at time t' will be (T−T02)=T1+T02
Putting these valuse in Eq (i) we have
T1−T02=T0+(T1−T0)−kt
or T1−T02=(T1−T0)e−ktore−kt=12ort'=In2k .
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL-I(H.W)19videos
TRANSMISSION OF HEAT
- BOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL-II(C.W)27videos
TRANSMISSION OF HEAT
- BOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - SINGLE ANSWER QUESTIONS Passage -11videos
TRANSMISSION OF HEAT
- BOOK - NARAYNACHAPTER - THERMODYNAMICSEXERCISE - Exercise187videos
THERMODYNAMICS
- BOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - STATEMENT TYPE QUESTION23videos
UNITS AND MEASUREMENTS
Similar Questions
A hot fbody placed in air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being k times the temperature difference from the surrounding. Starting from t=0 , find the time in which the body will loss half the maximum heat it can lose.
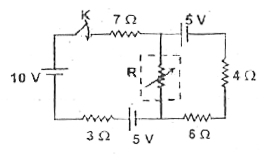
View SolutionIn the circuit shown the resistance R is kept in a chamber whose temperature. is 20∘C which remains constant. The initial temperature and resistance of R is 50∘C and 15Ωrespectively. The rate of change of resistance R with temperature is 12Ω/∘C and the rate of decrease of temperature of R is In(3/100) times the temperature difference from the surrounding (Assume the resistance R loses heat only in accordance with Newton's law of cooling) If K is closed at t = 0, then find the
(a) value of. R for which power dissipation in it is maximum.
(b) temperature of R when power dissipation is maximum
(c) time after which the power dissipation will be maximum
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
According to Newton's law of cooling, the body cools from 100∘C→60∘C in 20 minutes. The temperature of the surrounding being 20∘C The body cool down to 30∘C in
A40 minutesB50 minutesC90 minutesD60 minutes - Question 2 - Select One
According to Newton's law of cooling, the body cools from 80∘Cand50∘C at room temperature of 25∘C in 30 minutes. After 1 hours, the temperature of the body is
A11.36∘CB18.18∘CC36.36∘CD22.72∘C - Question 3 - Select One
According to Newton’s law of cooling, the rate of cooling of a body is proportional to (Δθ)n , where Δθis the difference of the temperature of the body and the surrounding, and n is equal to :
AOneBtwoCthreeDfour
Ac cording to Newton's law of cooling, the rate of cooling of a body is proportional to (Δθ)n, where Δθ is the difference of the temperature of the body and thae surrounding. What is the value of n out of 4,3,2,and 1?
View SolutionA hot body placed in a surrounding of temperature θ0 obeys Newton's law of cooling dθdt=−k(θ−θ0) . Its temperature at t=0 is θ1 the specific heat capacity of the body is s and its mass is m. Find (a) the maximum heat that the body can lose and (b) the time starting from t=0 in which it will lose 90% of this maximum heat.
View SolutionAccording to Newton's law of cooling, the rate of cooling of a body is proportional to (Δθ)n, where Δθ is the difference of the temperature of the body and the surroundings, and n is equal to
View SolutionAccording to Newton's law of cooling, the rate of cooling of a body is proportional to (Δθ)n, where Δθ is the difference of the temperature of the body and the surroundings, and n is equal to
View SolutionAssertion: According to Newton's law of cooling, the rate of loss of heat, −dQ/dt of the body is directly proportional to the difference of temperature.
Reason :This law holds for all type of temperature differences.View Solution

