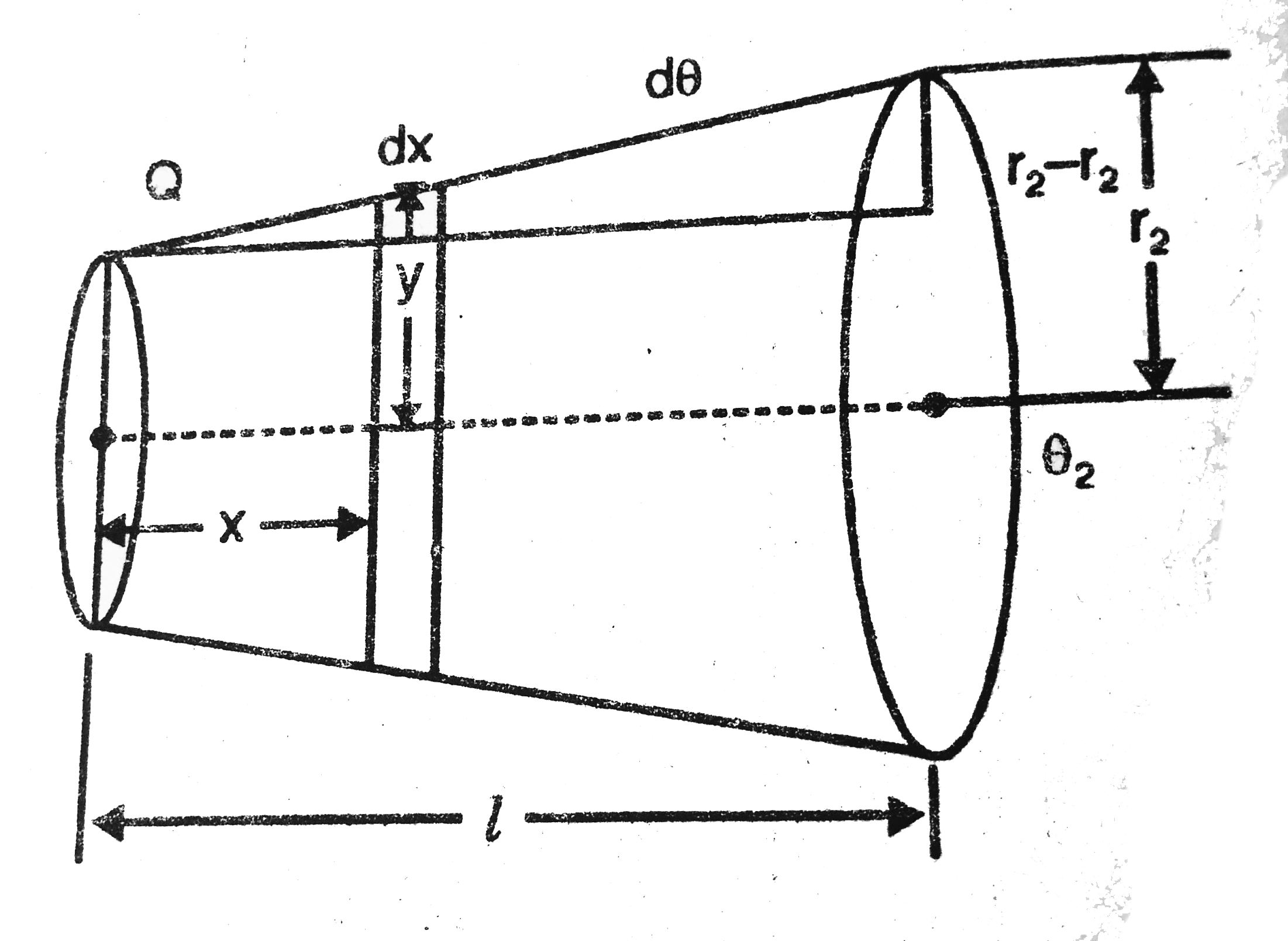
Find the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1 . Thermal conductivity of the material of the rod is K.

The correct Answer is:A, B
TenΦ=r2−r1L=y−r1x
D⇔erentat∈gw,r→x<br>r_2-r_1=(Ldy)/(dx)-0<br>implies(dy)/(dx)=(r_2-r_1)/L<br>implies(r_2-r_1)/(L)dx=(dyL)/(r_2-r_1) …(i)<br>(Q/t)=(k pi y^2 d theta )/(dx)<br>Now (Qdx)/t=(k pi y^2 d theta )/(dx)<br>implies(QLdy)/(t(r-2-r_1))=(k pi y^2 Delta theta )<br>[Fromequation(i)]
⇒dθ=QLdyt(r2−r1)kπy2
Intrgrating both side
⇒∫θ2θ1dθ=QLt(r2−r1)kπ∫r1r2(dy)/(y2)
⇒(θ2−θ1)=QLt(r2−r1)kπ×[−1y]r2r1
⇒(θ2−θ1)=QLt(r2−r1)kπ×[1r1−1r2]
⇒(θ2−θ1)=QLt(r2−r1)kπ(r2−r1)r2r1
⇒(Qt)=(kπ(r2r1)θ1−θ2L.
Topper's Solved these Questions
- HEAT TRANSFERBook:HC VERMAChapter:HEAT TRANSFERExercise:EXERCIESE
Explore 1 Video
- HEAT TRANSFERBook:HC VERMAChapter:HEAT TRANSFERExercise:Objective 2
Explore 6 Videos
- HEAT AND TEMPERATUREBook:HC VERMAChapter:HEAT AND TEMPERATUREExercise:Exercise
Explore 4 Videos
- INTRODUCTION TO PHYSICSBook:HC VERMAChapter:INTRODUCTION TO PHYSICSExercise:Exercises
Explore 19 Videos
Similar Questions
A hole of radius r1 is made centrally in a uniform circular disc of thickness d and radius r2 . The inner surface (a cylinder of length d and radius r1 is maintained at a temperature θ1 and the oouter surface (a cylinder of length d and radius r2 . The is maintianed at a temperature θ2(θ1>θ2) .The thermal conductivity of the material of the dics is K. Calculate the heat flowing per unit time through the disc.
View SolutionA metal rod of cross sectional area 1.0cm2 is being heated at one end. At one time , the temperature gradient is 5.0∘Ccm−1 at cross section A and is 2.5∘Ccm−1 at cross section B. calculate the rate at which the temperature is increasing in the part AB of the rod. The heat capacity of the part AB=0.40J∘C−1 , thermal conductivity of the material of the rod. K=200Wm−1C−1 . Neglect any loss of heat to the atmosphere.
View Solution
Knowledge Check
A composite rod made of three rods of equal length and cross-section as shown in fig. The thermal conductivites of the materials of the rods are K/2, 5K and K respectively. The end A and end B are at constant tempertures. All heat entering the face A goes out of the end B there being no loss of heat from the sides of the bar. The effective thermal conductivity of the bar is
 A15K/16B6K/13C5K/16D2K/3
A15K/16B6K/13C5K/16D2K/3A metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLThree bars each of area of cross section A and length L are connected in series as shown in the figure. Thermal conductivities of their materials are K, 2K and 1.5K. If the temperatures of free end of first and the last bar are 200∘C and 18∘C. The value of θ1 and θ2 are (in steady state):
A120∘C,80∘CB116∘C,80∘CC116∘C,74∘CD120∘C,74∘C
Heat is flowing through a rod of length 25.0cm having cross-sectional area 8.80cm2. The coefficient of thermal conductivity for the material of the rod is K=9.2×10−2kcals−1m−1.∘C−1. The Temperatures of the ends of the rod are 125∘C and 0∘C in the steady state. Calculate (i) temeprature gradient in the rod (ii) temperature of a point at a distance of 10.0cm from the hot end and (iii) rate of flow of heat.
View Solution(a) Three rod of lengths 20cm each and area of cross-section 1cm2 are joined to form a triangle ABC. The conductivities of the rods are KAB=50J/m−s−.∘C,KBC=200J/m−s−.∘C and KAC=400J/m−s−.∘C. The junctions A,B and C are maintained at 40∘C, 80∘C and 80∘C respectively. Find the rate of heat flowing through the rods AB,AC and BC.
(b) A semicircular rod is joineted as its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross-section of the simicircular rod to the heat transferred through a cross-section of the straight rod in a given time.
View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionThe ratio of the areas of cross-section of two rods of different materials is 1:2, and the ratio of the thermal conductivities of their materials is 4:3. On keeping equal temperature-difference between the ends of these rods, the rate of conduction of heat are equal. Determine the ratio of the lengths of the rods.
View SolutionTwo rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.

View Solution
