Calculate the capacitance of a parallel plate capacitor, with plate area A and distance between the plates d, when filled with a dielectric whose permittivity varies as
∈(x)=∈0+kx(0<x<d2),∈(x)=∈0+k(d−x)(d2<x≤d).

The given capacitor is equivalent to two capacitors in series. Let C1 and C2 be their capacities. Then
1C=∫[1dC1+1dC2]
Consider an element of width dx at a distance x from the left plate. Then
dC1=(ε0+kx)Adxfor0<x<d2
and dC2={∈0+k(d−x)}Adxford2<x≤d
on substituting these two values we get
1C−∫1dC=2KAln(2∈0+Kd2∈0)⇒C=KA2ln(2∈0+Kd2∈0).
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - C.U.Q54videos
CAPACITANCE
- BOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Assertion & Reasoning16videos
CAPACITANCE
- BOOK - NARAYNACHAPTER - ATOMS EXERCISE - EXERCISE -447videos
ATOMS
- BOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)25videos
COMMUNICATION SYSTEM
Similar Questions
Calculate the capacitance of a parallel plate condenser, with plate area A and distance between plates d, when filled with a dielectric whose dielectric constant varies as,
K(x)=1+βx∈0 0<x<d2, K(x)=1+β∈0(d−x) d2<x<d.
For what value of β would the capacity of the condenser be twice that when it is without any dielectric?View SolutionThe plates of a parallel plate capacitance 1.0 F are separated by a distance d =1 cm. Find the plate area .
View Solution
Knowledge Check
- Question 1 - Select One
The capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
 Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d - Question 2 - Select One
The force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
ACV22dBC2V22d2CC2V2d2DV2dC
A parallel plate capacitor with plate area 'A' and distance of separation 'd' is filled with a dielectric. What is the capacity of the capacitor when permittivity of the dielectric varies as : ε(x)=ε0+kx, for (0<x≤d2)
ε(x)=e0+k(d−x), for (d2≤x≤d)View SolutionThe distance between the plates fo a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates, what will be the new capacity ?
View SolutionIn a parallel plate capacitor distance between the plate is 'd'. If dielectric of variable permeability is filled as
ε(x)=ε0+kx,0<x≤d2
ε(x)=ε0+k(d−x),d2<x≤d
Find capacitance.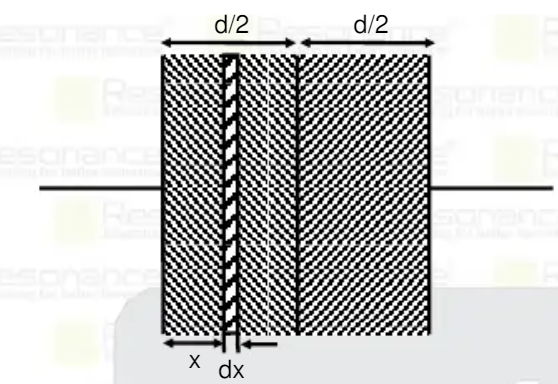 View Solution
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
 View Solution
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
 View Solution
View SolutionThe' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View Solution

