In a parallel plate capacitor distance between the plate is 'd'. If dielectric of variable permeability is filled as
ε(x)=ε0+kx,0<x≤d2
ε(x)=ε0+k(d−x),d2<x≤d
Find capacitance. 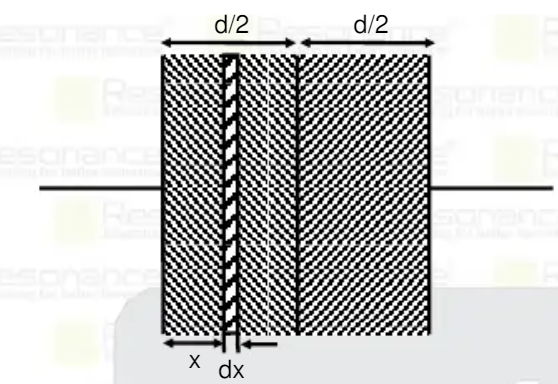
Step by step video & image solution for In a parallel plate capacitor distance between the plate is 'd'. If dielectric of variable permeability is filled as epsilon(x) = epsilon_0 + kx , 0< x le d/2 epsilon(x) = epsilon_0 + k(d-x) , d/2 < x le d Find capacitance. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
Calculate the capacitance of a parallel plate capacitor, with plate area A and distance between the plates d, when filled with a dielectric whose permittivity varies as
∈(x)=∈0+kx(0<x<d2),∈(x)=∈0+k(d−x)(d2<x≤d).
View SolutionThe gap between the plates of a parallel-plate capacitor is filled with istropic dielectrc whose permittlvity ε varies linearly from esπlon1 to ε2(ε2>ε1) in the direction perpendicular to the plates. The area of each plate equals S, the separation between the plates is equal to d. Find :
(a) the capacitance of the capacitor,
(b) the space density of the bound chagres as a function of a if the charge of the capacitor is q and E in it is directed toward the growing ε values.
View Solution
Knowledge Check
For all xε(0,1)
Aex<1+xBloge(1+x)<xCsinx>xDlogex>x−1A system of two parallel plates, each of area A, are separated by distance d1 and d2. The space between them is filled with dielectrices of permitivities ε1 and ε)2. The permittivity of free space is ε0. The equivalent capacitance of the system is
Aε1ε2Aε2d1+ε1d2Bε1ε2ε0Aε1d1+ε2d2Cε0Aε1d1+ε2d2Dε0Aε1d2+ε2d1A parallel-plate capacitor has plate area A, the distance between its two plates x and y is d and a dielectric slab of dielectric constant εr is filled between the regions. It is connected to a cell of emf E. If the dielectric slab is removed, then
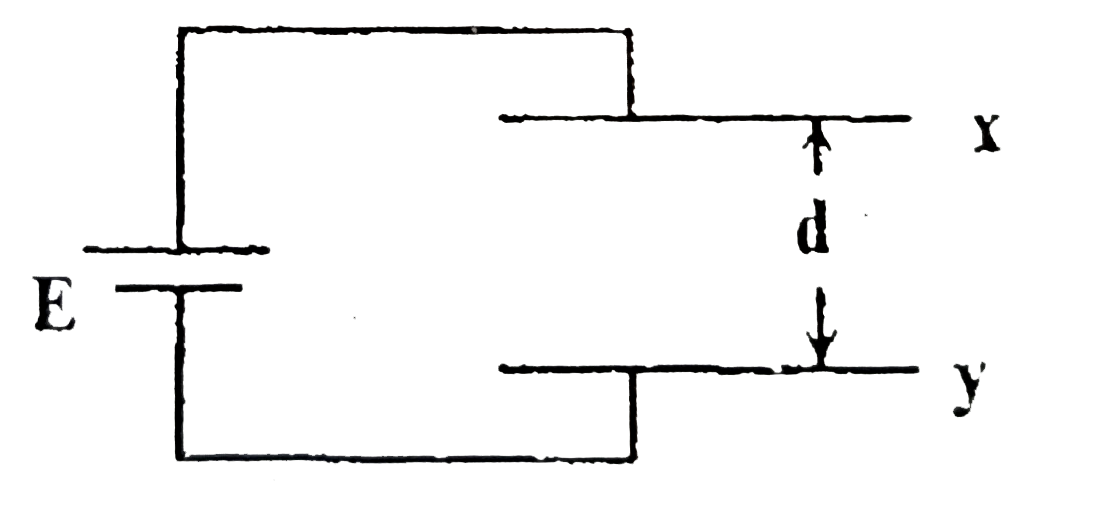 Aε0Ad[εr−1]E charge is absorbed by the cellBε0Ad[εr−1]E charge flows through the circuitCnegative charge flows from plate y to plate xDnegative charge flows from plate x to plate y
Aε0Ad[εr−1]E charge is absorbed by the cellBε0Ad[εr−1]E charge flows through the circuitCnegative charge flows from plate y to plate xDnegative charge flows from plate x to plate y
Calculate the capacitance of a parallel-plate capacitor of area S, separation d and dielectric constant varying linearly from ε1 to ε2(ε2>ε1) in the direction of the applied field.
View SolutionThree dielectrics of relative permittivities εr1=1,εr2=2, and εr3=3
are introduced in a parallel plate capacitor of plate A and B.
 .
.
View SolutionThe separation between the plates of a parallel plate capacitor is d and the area of each plate is A. iff a dielectric slab of thickness x and dielectric constant K is introduced between the plates, then the capacitance will be
View SolutionAssertion: The force with which one plate of a parallel plate capacitor is attracted towards the other plate is equal to square of surface density per ε per unit area.
Reason: The electric field due to one charged plate of the capacitor at the location of the other is equal to surface density per ε.
View SolutionParallel plate capacitor has capacitance C0=ε0Ad. When a insulating medium is added of dielectric constant K, the capacity becomes Cm=εAd=Kε0Ad=KC0. Let t be the thickness of dielectric such that :
t(<d), then the capacity is Cd=ε0Ad−t(1−1k). For metals, K=∞. Therefore, when a metal plate of thickness t<d is inctroduced, the capacity becomes C=ε0Ad−t.
If the distance between two parallel plates is doubled and area of the plates is halved, the capacitance increases by :
View Solution
