A highly conducting sheet of aluminium foil of negligible thickness is placed between the plates of a parallel plate capacitor. The foil is parallel to the plates. If the capacitance before the insertion of foil was 10μF, its value after the insertion of foil will be.
20μF
10μF
5μF
Zero
The correct Answer is:B
To solve the problem of finding the capacitance of a parallel plate capacitor after inserting a highly conducting sheet of aluminum foil, we can follow these steps:
1. Understand the Initial Setup:
- We have a parallel plate capacitor with an initial capacitance C0=10μF.
- The distance between the plates is d and the area of the plates is A.
2. Capacitance Formula:
- The capacitance of a parallel plate capacitor is given by the formula:
C=ϵ0Ad
- Here, ϵ0 is the permittivity of free space.
3. Inserting the Conducting Foil:
- When a highly conducting sheet (aluminum foil) of negligible thickness is placed between the plates, it effectively divides the capacitor into two capacitors in series.
- Each of these capacitors will have a distance of d2 between their plates.
4. Capacitance of Each Section:
- The capacitance of each section (let's call them C1 and C2) is:
C1=C2=ϵ0Ad2=2ϵ0Ad
- Since both sections are identical, we have C1=C2=2C0.
5. Total Capacitance in Series:
- The total capacitance C of two capacitors in series is given by:
1C=1C1+1C2
- Substituting C1 and C2:
1C=12C0+12C0=22C0=1C0
- Therefore, we find that:
C=C0
6. Final Result:
- Since the initial capacitance C0=10μF, the capacitance after the insertion of the foil remains:
C=10μF
Final Answer:
The value of the capacitance after the insertion of the foil will be 10μF.
- We have a parallel plate capacitor with an initial capacitance C0=10μF.
- The distance between the plates is d and the area of the plates is A.
- The capacitance of a parallel plate capacitor is given by the formula:
C=ϵ0Ad
- Here, ϵ0 is the permittivity of free space.
- When a highly conducting sheet (aluminum foil) of negligible thickness is placed between the plates, it effectively divides the capacitor into two capacitors in series.
- Each of these capacitors will have a distance of d2 between their plates.
- The capacitance of each section (let's call them C1 and C2) is:
C1=C2=ϵ0Ad2=2ϵ0Ad
- Since both sections are identical, we have C1=C2=2C0.
- The total capacitance C of two capacitors in series is given by:
1C=1C1+1C2
- Substituting C1 and C2:
1C=12C0+12C0=22C0=1C0
- Therefore, we find that:
C=C0
- Since the initial capacitance C0=10μF, the capacitance after the insertion of the foil remains:
C=10μF
The value of the capacitance after the insertion of the foil will be 10μF.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Level-II (C.W)14videos
CAPACITANCE
- BOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Level-III (C.W)41videos
CAPACITANCE
- BOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Assertion & Reasoning16videos
CAPACITANCE
- BOOK - NARAYNACHAPTER - ATOMS EXERCISE - EXERCISE -447videos
ATOMS
- BOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)25videos
COMMUNICATION SYSTEM
Similar Questions
A slab of copper of thickness b is inserted in between the plates of a parallel plate capacitor as shown in figure. The separation of the plates is d. If b=d/2, then the ratio of capacities of the capacitor after and before inserting the slab will be
 View Solution
View SolutionA sheet of aluminium foil of negligible thickness is placed between the plates of a capacitor of capacitance C as shown in the figure then capacitance of capacitor becomes
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A sheet of aluminium foil of negligible thickness is placed between the plates of a capacitor of capacitance C as shown in the figure then capacitance of capacitor becomes
 A(a) decreasesB(b) remains unchangedC(c) becomes infiniteD(d) increases
A(a) decreasesB(b) remains unchangedC(c) becomes infiniteD(d) increases - Question 2 - Select One
A dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
Abecomes zeroBremains the sameCdecreasesDincreases - Question 3 - Select One
A sheet of aluminium foil of negligible thickness is placed between the plates of a capacitor of capacitance C as shown in the figure, the capacitance of capacitor becomes
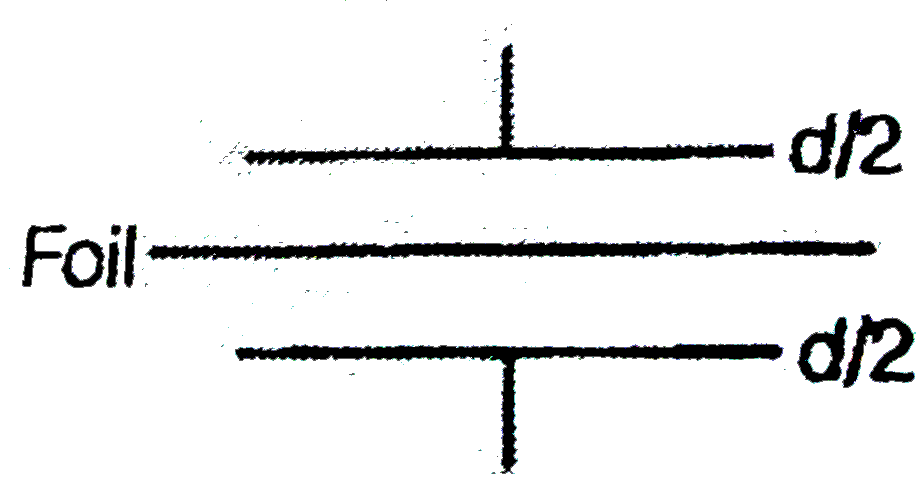 A2CBCCC2Dzero
A2CBCCC2Dzero
A metal foil of negligible thickness is introduced between the two plates of a capacitor at the centre. The capacitance of capacitor will be
View SolutionTo reduce the capacitance of parallel plate capacitor, the space between the plate is
View SolutionIf a thin metal foil of same area is placed between the two plates of a parallel plate capacitor of capacitance C, then new capacitance will be
View SolutionA parallel plate capacitor is connected to a cell. A metal plate of negligible thickness is inserted parallel to plates.
(A) the capacitance remains same
(B) the cell will supply more charge
(C) equal and opposite charges will appear pm two faces of metal plate
(D) the potential difference between the plates will increaseView SolutionA slab of copper of thickness b is inserted in between the plates of parallel plate capacitor as shown in figure. The separation of the plate is d. If b=d/2, then the ratio of capacities of the capacitor after and before inserting that slab will be
 View Solution
View Solution

