A radio capacitor of variable capacitance is made of n parallel plates each of area A and separated from each other by a distanced. The alternate plates are connected together. The capacitance of the combination is.
nA∈od
(n−1)A∈od
(2n−1)A∈od
(n−2)A∈od
The correct Answer is:B
To find the capacitance of a variable capacitor made of n parallel plates, where alternate plates are connected together, we can follow these steps:
Step 1: Understanding the Configuration
In this setup, we have n parallel plates, and alternate plates are connected together. This means that if we have n plates, they can be grouped into pairs of connected plates.
Step 2: Counting the Number of Capacitors
Since alternate plates are connected, we can think of the configuration as consisting of n2 capacitors in parallel (if n is even). Each capacitor is formed by two adjacent plates.
Step 3: Capacitance of Each Capacitor
The capacitance \( C \) of a single capacitor formed by two adjacent plates can be calculated using the formula for the capacitance of parallel plates:
\(
C = \frac{\varepsilon_0 A}{d}
\)
where:
- \( \varepsilon_0 \) is the permittivity of free space,
- \( A \) is the area of each plate,
- \( d \) is the separation between the plates.
Step 4: Total Capacitance of the Configuration
Since we have \( n/2 \) capacitors in parallel, the total capacitance \( C_{total} \) of the configuration can be calculated as:
\(
C_{total} = \frac{n}{2} C
\)
Substituting the value of \( C \) from Step 3:
\(
C_{total} = \frac{n}{2} \left(\frac{\varepsilon_0 A}{d}\right)
\)
Step 5: Final Expression
Thus, the final expression for the total capacitance of the variable capacitor configuration is:
\(
C_{total} = \frac{n \varepsilon_0 A}{2d}
\)
Summary
The capacitance of the combination of n parallel plates, where alternate plates are connected together, is given by:
\(
C_{total} = \frac{n \varepsilon_0 A}{2d}
\)
---
In this setup, we have n parallel plates, and alternate plates are connected together. This means that if we have n plates, they can be grouped into pairs of connected plates.
Since alternate plates are connected, we can think of the configuration as consisting of n2 capacitors in parallel (if n is even). Each capacitor is formed by two adjacent plates.
The capacitance \( C \) of a single capacitor formed by two adjacent plates can be calculated using the formula for the capacitance of parallel plates:
\(
C = \frac{\varepsilon_0 A}{d}
\)
where:
- \( \varepsilon_0 \) is the permittivity of free space,
- \( A \) is the area of each plate,
- \( d \) is the separation between the plates.
Since we have \( n/2 \) capacitors in parallel, the total capacitance \( C_{total} \) of the configuration can be calculated as:
\(
C_{total} = \frac{n}{2} C
\)
Substituting the value of \( C \) from Step 3:
\(
C_{total} = \frac{n}{2} \left(\frac{\varepsilon_0 A}{d}\right)
\)
Thus, the final expression for the total capacitance of the variable capacitor configuration is:
\(
C_{total} = \frac{n \varepsilon_0 A}{2d}
\)
The capacitance of the combination of n parallel plates, where alternate plates are connected together, is given by:
\(
C_{total} = \frac{n \varepsilon_0 A}{2d}
\)
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Level-II (C.W)14videos
CAPACITANCE
- BOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Level-III (C.W)41videos
CAPACITANCE
- BOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Assertion & Reasoning16videos
CAPACITANCE
- BOOK - NARAYNACHAPTER - ATOMS EXERCISE - EXERCISE -447videos
ATOMS
- BOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)25videos
COMMUNICATION SYSTEM
Similar Questions
Knowledge Check
- Question 1 - Select One
The capacitance of a parallel plate capacitor can be increased by
Aincreasing the area of the plates.Bdecreasing the distances between the plates.Cusing a dielectric of higher permittivity.Dall the above. - Question 2 - Select One
Capacitance of a parallel plate capacitor can be increased by
Aincreasing the distance between the platesBdecreasing the distance between the platesCdecreasing the area of platesDincreasing the thickness of the plates - Question 3 - Select One
If area of each plate is A and plates are separated from each other by a distance d then Ceq. between A and B is -
 A3∈0AdB∈0A3dC3∈0A2dD2∈0A3d
A3∈0AdB∈0A3dC3∈0A2dD2∈0A3d
Combination of capacitors and Capacitance of combination of parallel plates
View SolutionFive identical capacitor plates, each of surface area 'A', are arranged such that adjacent plates are at distance 'd' apart. The alternate plates are joined together as shown in Fig. The capacitance of the arrangement is __________ .
 View Solution
View SolutionThe plates of a parallel plate capacitance 1.0 F are separated by a distance d =1 cm. Find the plate area .
View SolutionA parallel-plate capacitor is made up of 11 metal plates each of area 15 cm2 separated by sheets of mica of realative permittivity 6 and thickness 0.2 mm, the altemate plates being joined together. Calculate the capacitance of the capacitor in microfarad.
[Hint: There will be (n-1) similar parallel plate capactions of capacitance ε0εrAd
∴C=(n−1)ε0εrAd]View SolutionSix metallic plated each with a surface area of one side A. are placed at a distanced d from each other. The alternate plates are connected to points P and Q as shown in figure :
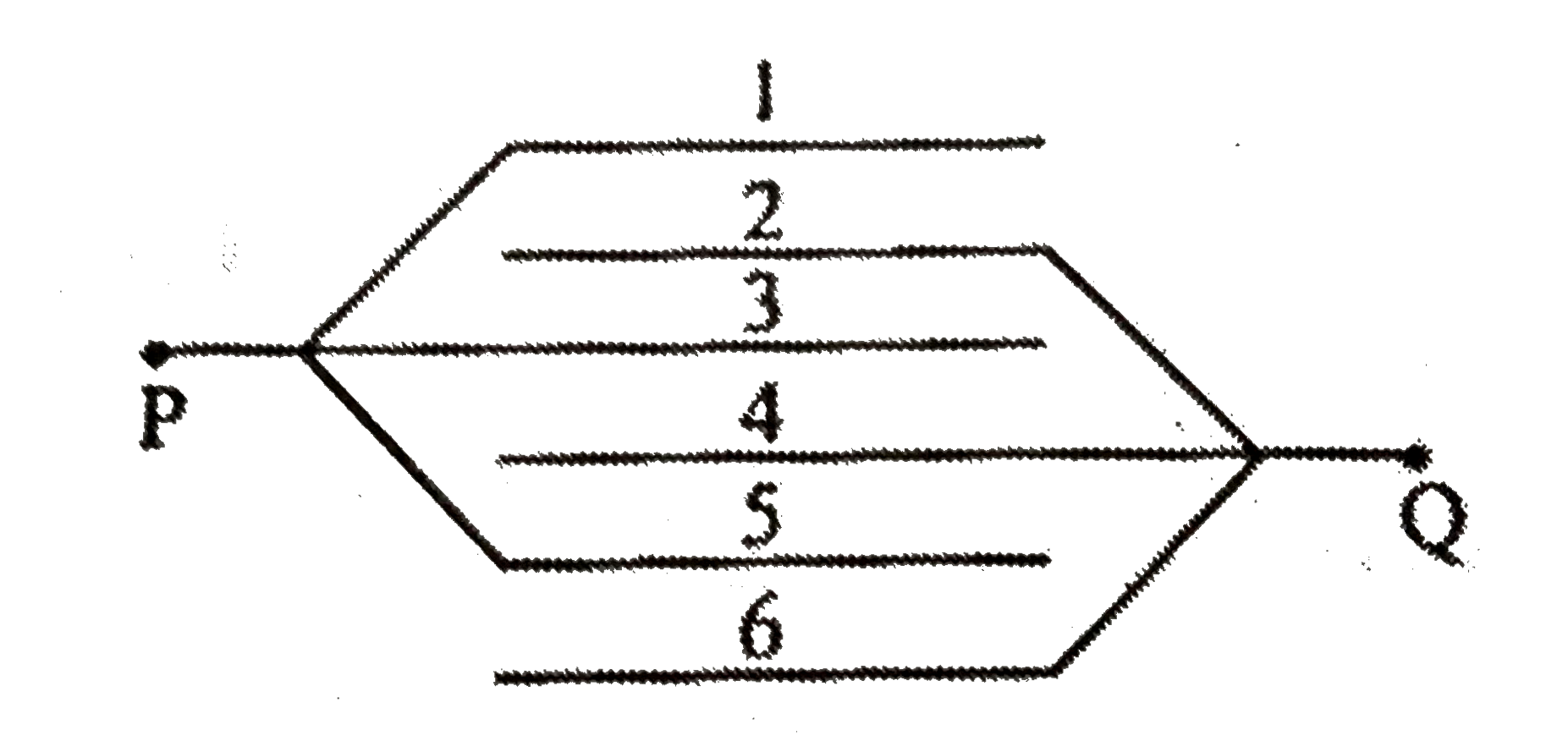
The capacitance of the system is :View Solution

