Match the following column.

Choose the correct option regarding above column.
A
ABCD3124
B
ABCD3214
C
ABCD2125
D
ABCD3214
Text Solution
The correct Answer is:B
Applying equations of motions in rotational motion, we get
x=x0+v0t+12at2→θ=θ0+ω0t+12αt2
v2=v20+2a(x−x0)→ω2=ω20+2α(θ−θ0)
v=v0+at→ω=ω0+αt
x,vanda→θ,ωandα.
Here, ω=dθdtandα=dωdt
A→3,B→2,C→1,D→5
|
Topper's Solved these Questions
- ROTATIONAL MOTION'BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - MHT CET Corner
35 Videos
- ROTATIONAL MOTION'BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - PRACTICE EXERCISE (Exercise 1 (TOPICAL PROBLEMS))
70 Videos
- REFRACTION OF LIGHTBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 2
25 Videos
- SCALARS AND VECTORS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SCALARS AND VECTORS EXERCISE - Exercise 2 (Miscellaneous Problems)
20 Videos
Similar Questions
Knowledge Check
Match the following columns and choose the correct option.
 A
A B
B C
C D
D
Match the following columns and choose the correct option.
 A
A B
B C
C D
D
Match the following columns and choose the correct option.
 A
A B
B C
C D
D
Match the following columns and choose the correct option.

View SolutionMatch the following columns and choose the correct option .

View SolutionMatch the column I with column II and choose the correct option.
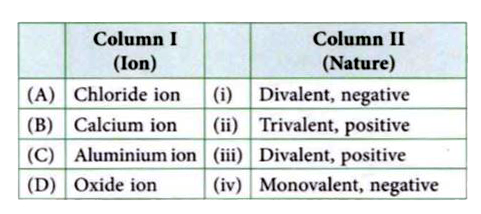
View SolutionMatch the column I with column II and choose the correct option.
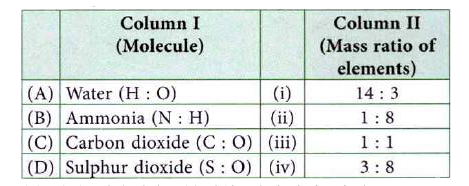
View SolutionMatch the column I with column II and choose the correct option

View Solution
