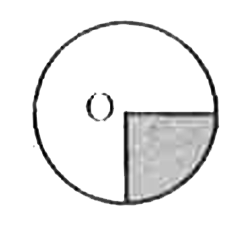
The Ml of a disc of mass M and radius R, about an axis passing through the centre O and perpendicular to the plane of the disc is $\frac{M R^{2}}{2}$ . If one quarter of the disc is removed, the new moment of inertia of the disc will be

A

$\frac{M R^{2}}{3}$

B

$\frac{M R^{2}}{4}$

C

$\frac{3}{8} M R^{2}$

D

$\frac{3}{2} M R^{2}$

Text Solution

Verified by Experts

The correct Answer is:C

Ml of the disc of mass $M = l = \frac{1}{2} M R^{2}$
When a quarter of the protion is removed, the new mass
$= \frac{3}{4} M = M'$
$∴$ New Ml $= \frac{1}{2} M' R^{2} = \frac{1}{2} (\frac{3}{4} M) R^{2} = \frac{3}{8} M R^{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS ROTATIONAL MOTION'

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The moment of inertia of a circular disc about an axis passing through the circumstances perpendicular to the plane of the disc is
A $(M R^{2}$
B $\frac{3}{2} M R [^(2)$
C $\frac{M R^{2}}{2}$
D $\frac{5}{4} M R^{2}$
Question 2 - Select One
The moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:

A $\frac{M R^{2}}{2}$
B $\frac{7 M R^{2}}{12}$
C $\frac{7 M R^{2}}{6}$
D $\frac{5 M R^{2}}{12}$
Question 3 - Select One
The radius of gyration of a uniform disc of radius R, about an axis passing through a point $\frac{R}{2}$ away from the centre of disc, and perpendicular to the plane of disc is:
A $\sqrt{\frac{1}{2}} R$
B $\sqrt{2} R$
C $\frac{\sqrt{3}}{2} R$
D $\frac{\sqrt{3}}{4} R$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-ROTATIONAL MOTION'-PRACTICE EXERCISE (Exercise 2 (MISCELLANEOUS PROBLEMS))

Home
Ask Doubt
Profile