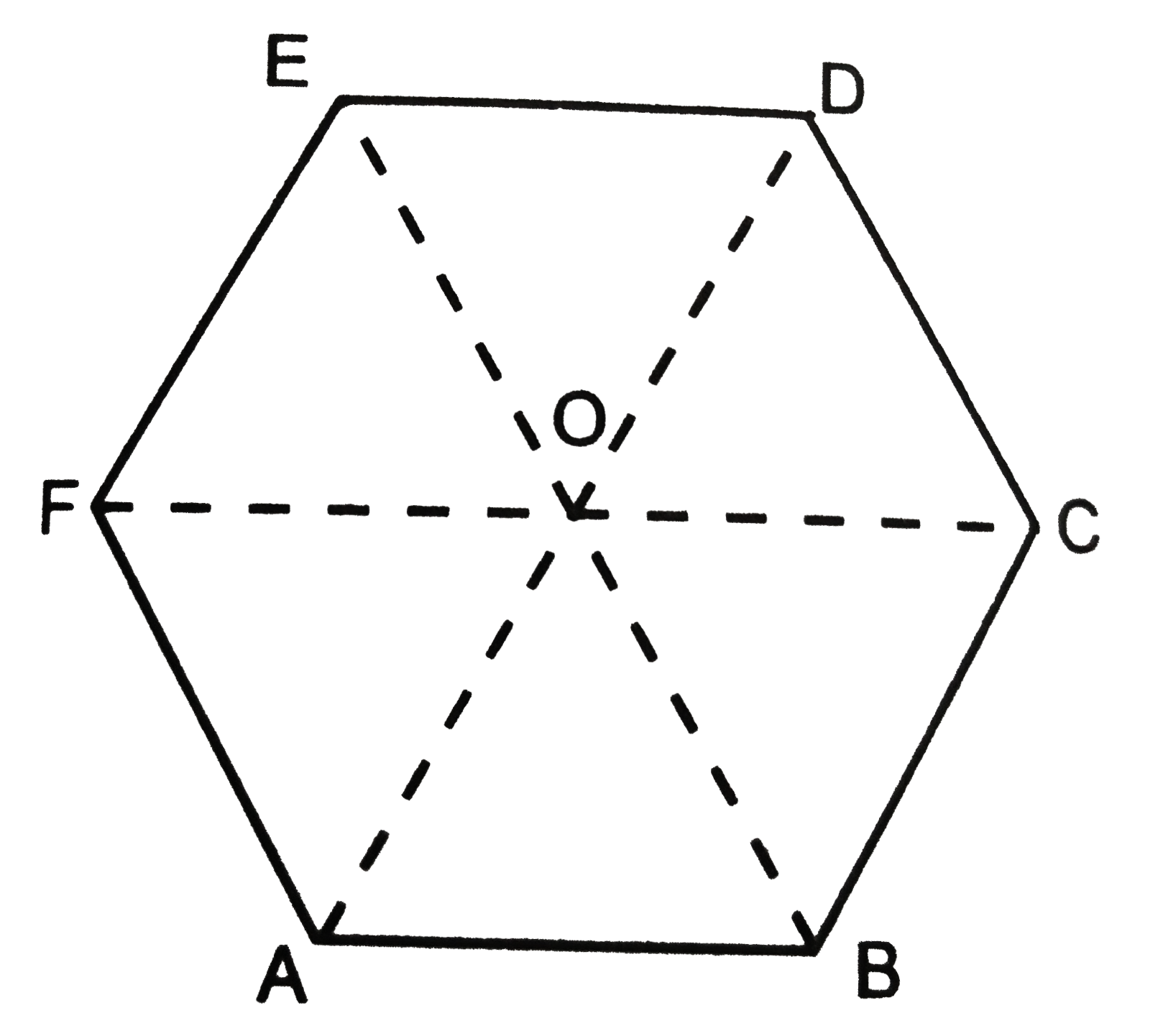
ABCDEF is a regular hexagon, Fig. 2 (c ) .65. What is the value of
(−−→AB+−−→AC+−−→AD+−−→AE+−−→AF?
 .
.
A
−−→AO
B
2−−→AO
C
4−−→AO
D
6−−→AO
Video Solution
Text Solution
The correct Answer is:D
−−→AB+−−→AC+−−→AD+−−→AE+−−→AF
=−−→AB+(−−→AB+−−→BC+−−→CD)
+(−−→AB+−−→BC+−−→CD+−−→DE)
+(−−→AB+−−→BC+−−→CD+−−→DE+−−→EF)
−−→AB=−−−→DE,−−→EC=−−−→EF
=3(−−→AB+−−→BC+−−→CD)=3(−−→AD)=6−−→AO
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCDEF is a regular hexagon with point O as centre. The value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF is
A2−−→AOB2−−→AOC6−−→AOD0 - Question 2 - Select One
If ABCDE is a pentagon, then
−−→AB+−−→AE+−−→BC+−−→DC+−−→ED+−−→AC is equal toA4−−→ACB2−−→ACC3−−→ACD5−−→AC - Question 3 - Select One
Consider the ragular hexagon ABCDEF with centre at O (origin).
Five forces −−→AB,−−→AC,−−→AD,−−→AE,−−→AF act at the vertex A of a regular hexagon ABCDEF. Then their resultant isA3−−→AOB2−−→AOC4−−→AOD6−−→AO
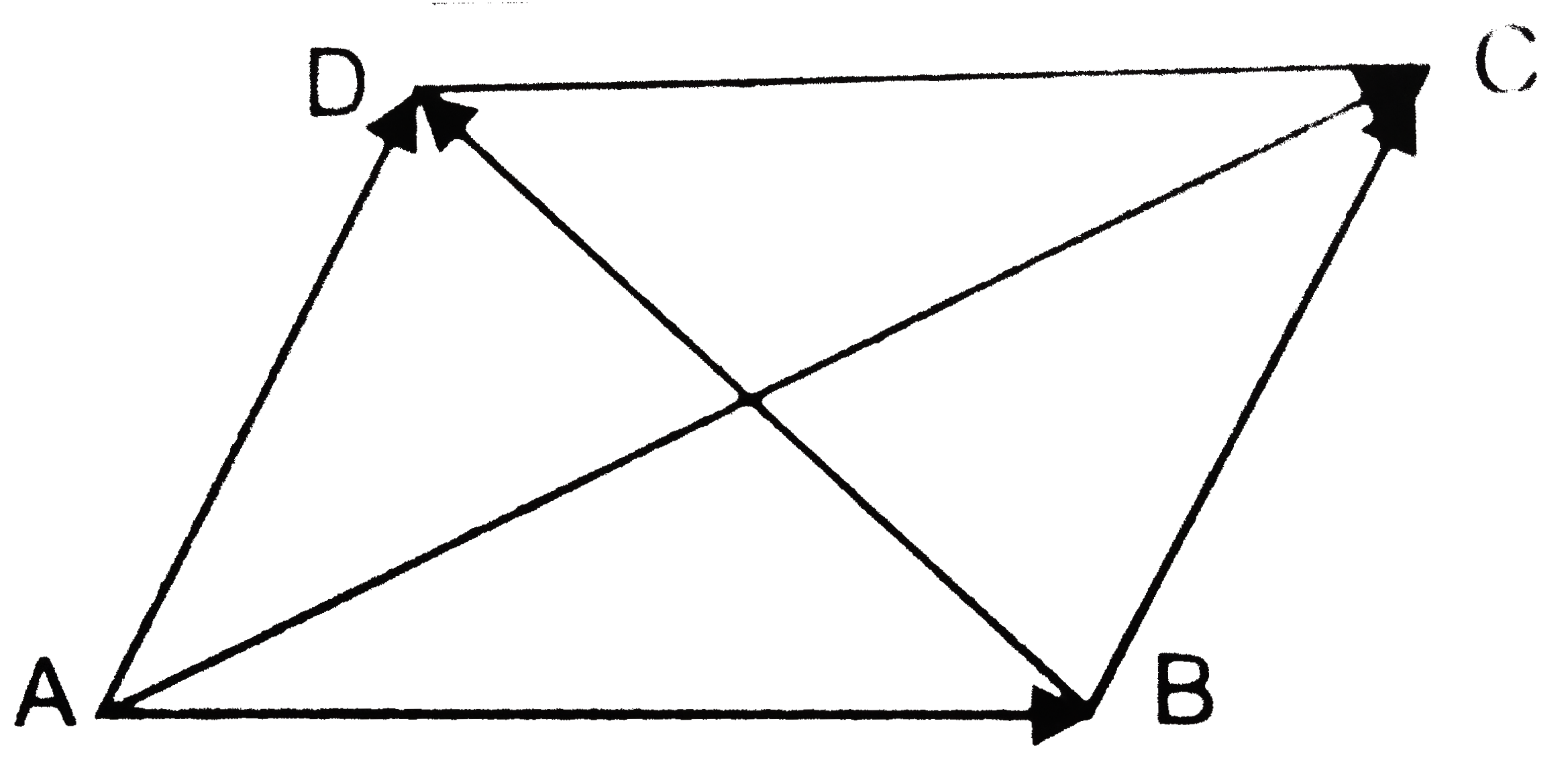
ABCD is a parallelogram Fig. 2 (c ) .64. ACand(BD)areitsdiagonals.Showtˆ<br> (a) vec (AC) +vec (BD) =2 vec (BC)<br>(b)vec (AC) - vec (BD) =2 vec (AB)
 . View Solution
. View SolutionABCDEF be a regular hexagon in the xy-plane and −−→AB=4ˆi then →CD =
View SolutionABCDEF is a regular hexagon with centre a the origin such that −−→AB+−−→EB+−−→FC=λ−−→ED then λ= (A) 2 (B) 4 (C) 6 (D) 3
View SolutionABCDEF is a regular hexagon. Find the vector →AB+→AC+→AD+→AE+→AF in terms of the vector →AD
View SolutionIn a regular hexagon ABCDEF, prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=3−−→AD
View Solution

