A uniform rope of is lying over a table. If the coefficient of friction be , then the maximum length of the part of the rope which can overhang the edge without sliding is
The correct Answer is:A
Let m: mass of chain
The chain will remain at rest , if
(##CPS_V01_C07_E01_034_S01.png" width="80%">
Topper's Solved these Questions
Similar Questions
A homogeneous chain of length L lie on a table. If the coefficent of friction is μ , find the maximum length L1 of the chain which can hang from the edge of the table without the chain sliding down.
(b) Consider the situation as shown in the figure. Find teh minimum value of m so that the blocks do not move.
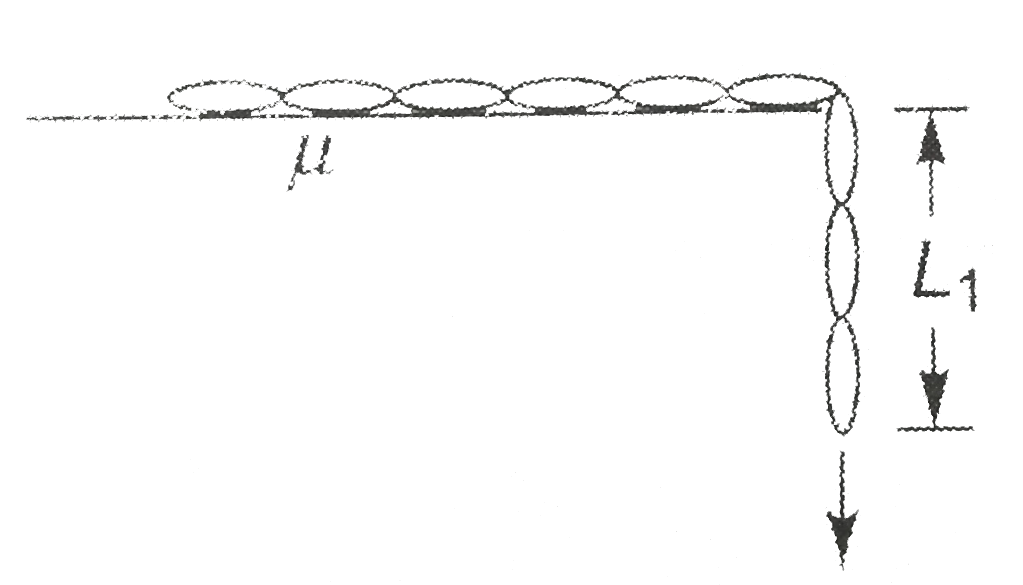

View SolutionAssuming the length of a chain to be L and coefficient of static friction μ. Compute the maximum length of the chain which can be held outside a table without sliding.
View Solution
Knowledge Check
A uniform rope of length l lies on a table . If the coefficient of friction is μ , then the maximum length l1 of the part of this rope which can overhang from the edge of the table without sliding down is :
A1μB1μ+1Cμlμ+1Dμlμ−1A uniform rope of length l lies on a table. If the coefficient of friction is μ, then the maximum length L of the part of this rope which can overhang from the edge of the table without sliding down is
AlμBlμ+1Cμl1+μDμlμ−1A uniform rope of length l lies on a table if the coefficient of friction is , then the maximum length l, of the part of this rope which can over hang from the edge of the table without sliding down is -
AlμBlμ+1Cμlμ+1Dμlμ−1
Assuming the length of a chain to be L and coefficient of static friction μ. Compute the maximum length of the chain which can be held outside a table without sliding.
View SolutionIf the coefficient of static friction between a table and a uniform massive rope is μ, what fraction of the rope can hang over the edge of a table without the rope sliding.
View SolutionA heavy uniform chain lies on horizontal table top. If the coeficient of friction 0.25, then the maximum friction of length of the chain that can hang over on edge of the table is
View SolutionA homogoneous chain of length L lies on a table. The coefficient of friction between the chain and the table is μ. The maximum length which can hang over the table in equilibrium is
View SolutionA uniform rope of length l and mass m lies on a smooth horizontal table with its length perpendicular to the edge of the table and a small part of the rope having over the edge. The rope starts sliding from rest under the weight of the over hanging end. The velocity of the rope when the length of the hanging part is . x
View Solution
