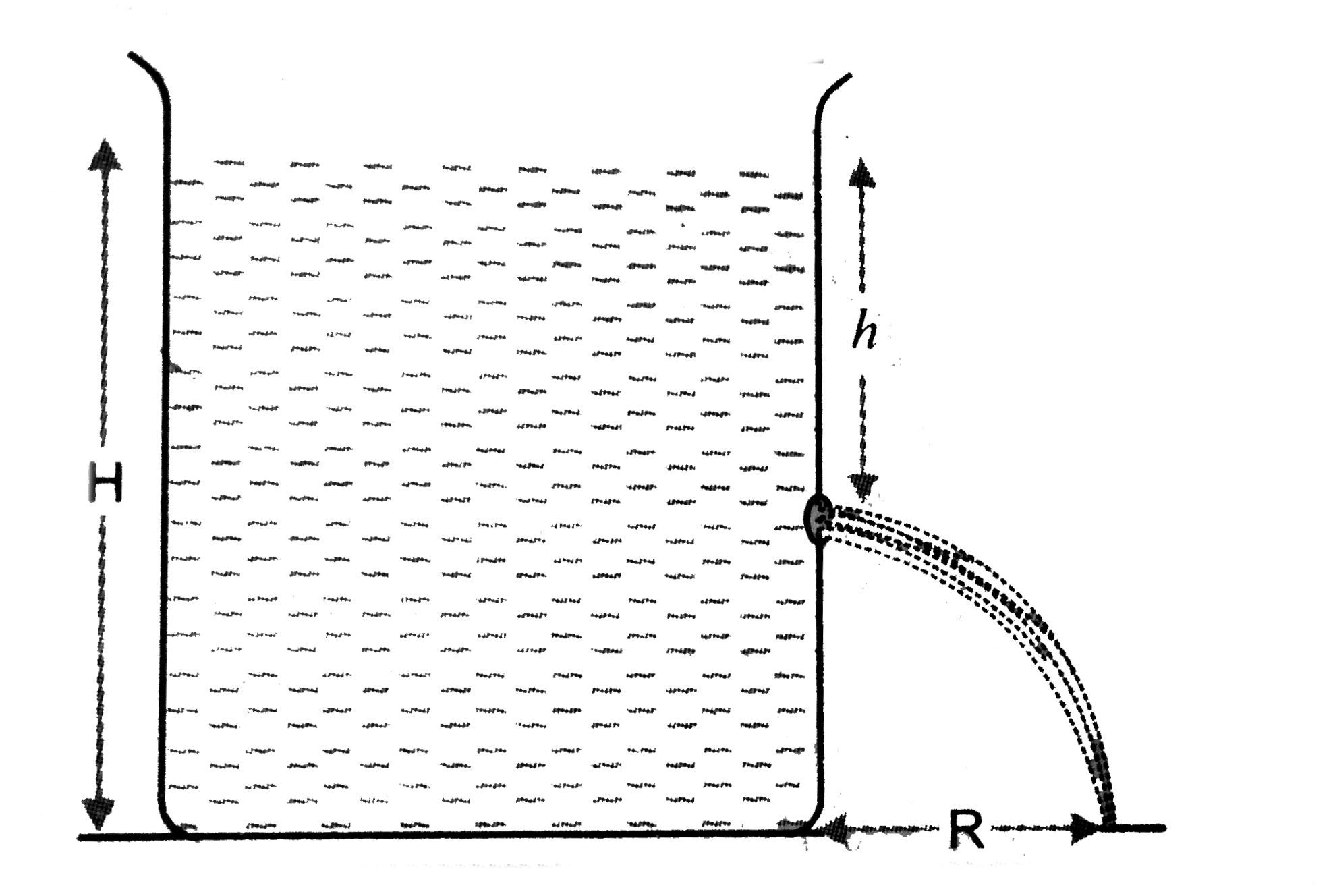
Water stands at a depth H in a tank whose side walls are vertical. A hole is made on one of the walls at a depth h below the water surface. Find at what distance from the foot of the wall does the emerging stream of water strike the floor and for what value of h this range is maximum ? What is the maximum possible range ?
To solve the problem, we need to determine the distance from the foot of the wall where the emerging stream of water strikes the floor and find the value of h that maximizes this distance.
1. Determine the velocity of the water at the hole:
The velocity of the water emerging from the hole can be calculated using Torricelli's theorem, which states that the speed V of efflux of a fluid under the force of gravity through an orifice is given by:
V=√2g(H−h)
where H is the total depth of water in the tank and h is the depth of the hole below the water surface.
2. Determine the time of flight:
The water will fall a vertical distance of H−h before it hits the ground. We can use the equation of motion for free fall:
H−h=12gt2
Rearranging gives us:
t2=2(H−h)g
Taking the square root:
t=√2(H−h)g
3. Calculate the horizontal distance (range):
The horizontal distance R that the water travels while falling can be calculated using:
R=V⋅t
Substituting the expressions for V and t:
R=√2g(H−h)⋅√2(H−h)g=2(H−h)
4. Maximize the range R:
To find the value of h that maximizes R, we need to differentiate R with respect to h and set the derivative to zero:
R=2(H−h)
The maximum occurs when:
dRdh=−2=0
This indicates that R is a linear function decreasing with h. Therefore, the maximum range occurs when h is minimized. The minimum value of h is 0 (when the hole is at the surface of the water).
5. Find the maximum range:
Substituting h=0 into the equation for R:
Rmax=2(H−0)=2H
Final Results:
- The distance from the foot of the wall where the water strikes the floor is given by:
R=2(H−h)
- The value of h that maximizes the range is h=0.
- The maximum possible range is:
Rmax=2H
The velocity of the water emerging from the hole can be calculated using Torricelli's theorem, which states that the speed V of efflux of a fluid under the force of gravity through an orifice is given by:
V=√2g(H−h)
where H is the total depth of water in the tank and h is the depth of the hole below the water surface.
The water will fall a vertical distance of H−h before it hits the ground. We can use the equation of motion for free fall:
H−h=12gt2
Rearranging gives us:
t2=2(H−h)g
Taking the square root:
t=√2(H−h)g
The horizontal distance R that the water travels while falling can be calculated using:
R=V⋅t
Substituting the expressions for V and t:
R=√2g(H−h)⋅√2(H−h)g=2(H−h)
To find the value of h that maximizes R, we need to differentiate R with respect to h and set the derivative to zero:
R=2(H−h)
The maximum occurs when:
dRdh=−2=0
This indicates that R is a linear function decreasing with h. Therefore, the maximum range occurs when h is minimized. The minimum value of h is 0 (when the hole is at the surface of the water).
Substituting h=0 into the equation for R:
Rmax=2(H−0)=2H
- The distance from the foot of the wall where the water strikes the floor is given by:
R=2(H−h)
- The value of h that maximizes the range is h=0.
- The maximum possible range is:
Rmax=2H
Topper's Solved these Questions
Similar Questions
Water stands at a depth H in a tank whose side walls are vertical. A hole is made in one of the walls at a height h below the water surface. The stream of water emerging from the hole strikes the floor at a distance R from the tank, where R is given by
View SolutionWater stands up height H in a tank, whose side walls are vertical. A hole is made on one of the walls does the emerging stream of water strike the floor and for what value of h this range is maximum ?
View Solution
Knowledge Check
Water stands at a height of 100 cm in a vessel whose side walls are vertical. A B and C are holes at height 80 cm, 50 cm, and 20 cm respectively from the bottom of the vessel. The correct system of flowing out is:
A B
B C
C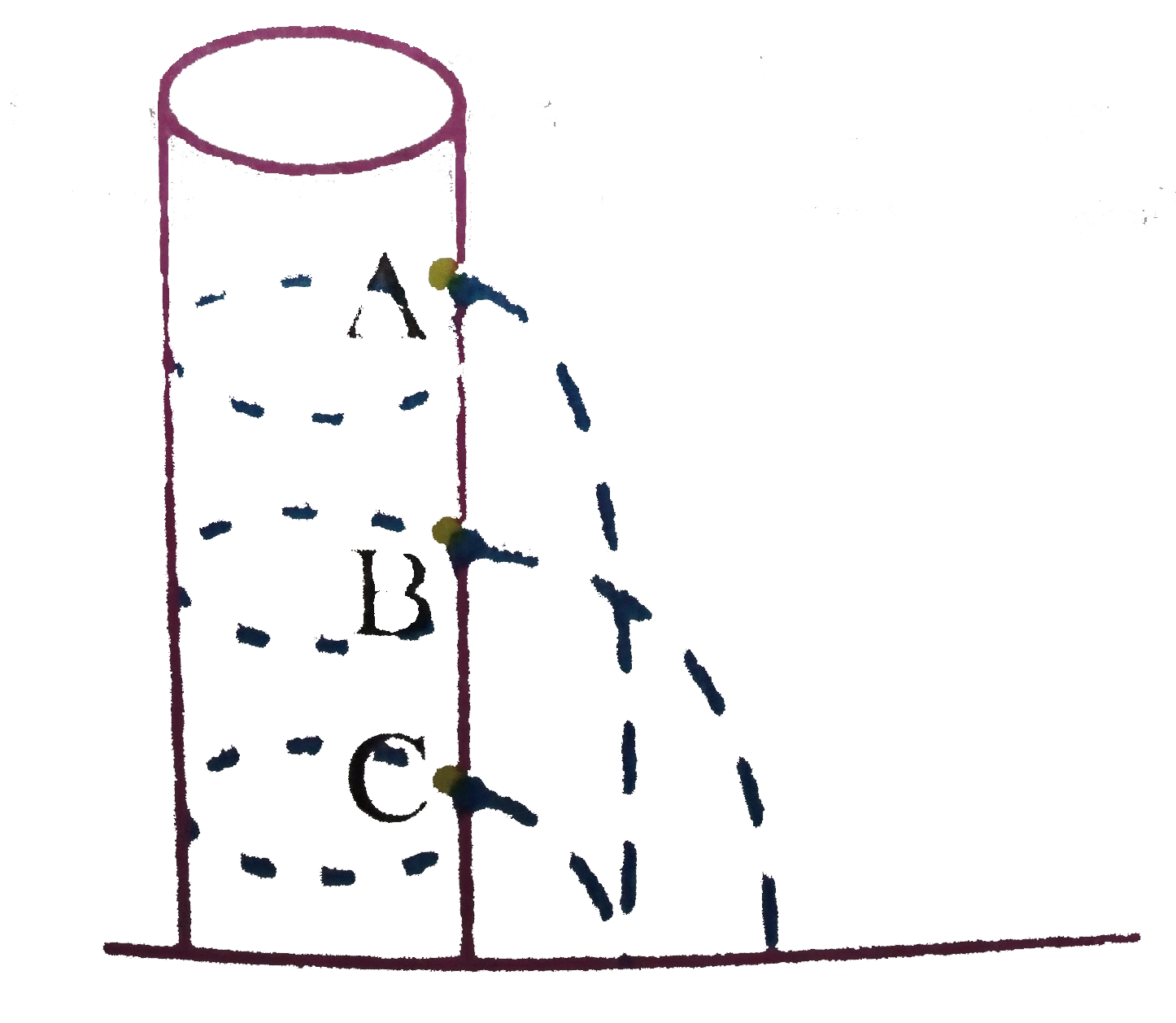 D
D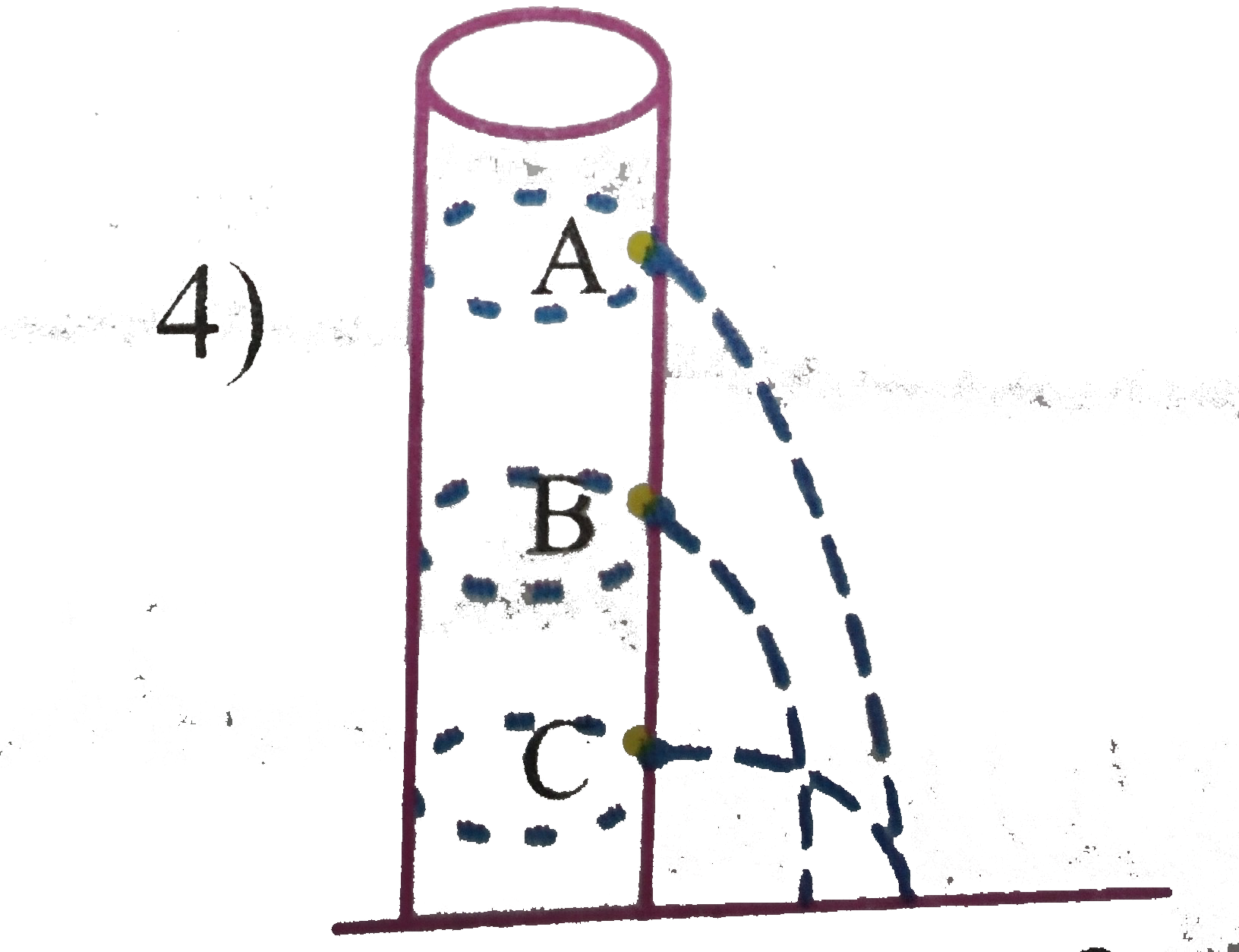
A tank is filled with water up to a height H. Water is allowed to come out of a hole P in one of the walls at a depth D below the surface of water. Express the horizontal distance x in terms of H and D
 .Ax=√D(H−H)Bx=√D(H−D)2Cx=2√D(H−D)Dx=4√D(H−D)
.Ax=√D(H−H)Bx=√D(H−D)2Cx=2√D(H−D)Dx=4√D(H−D)A tank if filled with water upto height H. When a hole is made at a distance h below the level of water. What will be the horizontal range of water jet ?
A2√h(H−h)B4√h(H+h)C4√h(H−h)D2√h(H+h)
The water is filled upto height of 12 m in a tank having vertical sidewalls. A hole is made in one of the walls at a depth 'h' below the water level. The value of 'h' for which the emerging stream of water strikes the ground at the maximum range is ___________m.
View SolutionWater stand at a heigh H in a tank whose sides are vertical. An orifice is made at the depth h on one of the wall Fig. 7(c).25. The emerging stream of water strikes at the distance R from the tank on the floor./ Find the relation for R in term of h, and H. When R is maxmimum, how h and H are related.
View SolutionA tank is filled with water to a height H. A hole is punched in the wall at a depth h below the water surface. Find the distance x from the wall at which the stream strikes the floor. Could a hole be punched at another depth so that this second stream would have the same range? If so at what depth? For what value of h is range maximum?
View SolutionA stream of water escapes from a hole 2m above the base of a tank and strikes the ground at a horizontal distance of 6m .The depth of the hole from the free surface of water is
View SolutionA point source is placed at a depth h below the surface of water (refractive index =μ). The medium above the surface of water is air from water.
View Solution
