A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
To find the difference in height of the liquid at the center of the cylindrical vessel and its sides when the vessel is rotated, we can follow these steps:
Step 1: Understand the problem
When a cylindrical vessel containing liquid is rotated, the liquid experiences a centrifugal force that causes it to rise at the sides. We need to calculate the height difference between the center and the sides of the vessel.
Step 2: Gather the given data
- Radius of the vessel, r=0.05m
- Speed of rotation, f=2rev/s
Step 3: Convert the speed of rotation to angular velocity
Angular velocity ω in radians per second can be calculated using the formula:
ω=2πf
Substituting the value of f:
ω=2π×2=4πrad/s
Step 4: Calculate the centrifugal acceleration
The centrifugal acceleration ac at a distance r from the axis of rotation is given by:
ac=ω2r
Substituting the values:
ac=(4π)2×0.05
Calculating (4π)2:
(4π)2=16π2≈157.913
Now substituting this back:
ac=157.913×0.05≈7.89565m/s2
Step 5: Relate the height difference to the centrifugal acceleration
The height difference h between the center and the sides of the liquid can be found using the hydrostatic pressure balance:
h=acgr
Where g is the acceleration due to gravity, approximately 9.81m/s2. Now substituting the values:
h=7.895659.81×0.05
Calculating 7.895659.81:
7.895659.81≈0.803
Now substituting back:
h=0.803×0.05≈0.04015m
Step 6: Final result
The difference in height of the liquid at the center of the vessel and its sides is approximately:
h≈0.04015m or 4.015cm
Summary
The height difference between the center and the sides of the liquid in the rotating cylindrical vessel is approximately 4.015 cm.
---
When a cylindrical vessel containing liquid is rotated, the liquid experiences a centrifugal force that causes it to rise at the sides. We need to calculate the height difference between the center and the sides of the vessel.
- Radius of the vessel, r=0.05m
- Speed of rotation, f=2rev/s
Angular velocity ω in radians per second can be calculated using the formula:
ω=2πf
Substituting the value of f:
ω=2π×2=4πrad/s
The centrifugal acceleration ac at a distance r from the axis of rotation is given by:
ac=ω2r
Substituting the values:
ac=(4π)2×0.05
Calculating (4π)2:
(4π)2=16π2≈157.913
Now substituting this back:
ac=157.913×0.05≈7.89565m/s2
The height difference h between the center and the sides of the liquid can be found using the hydrostatic pressure balance:
h=acgr
Where g is the acceleration due to gravity, approximately 9.81m/s2. Now substituting the values:
h=7.895659.81×0.05
Calculating 7.895659.81:
7.895659.81≈0.803
Now substituting back:
h=0.803×0.05≈0.04015m
The difference in height of the liquid at the center of the vessel and its sides is approximately:
h≈0.04015m or 4.015cm
The height difference between the center and the sides of the liquid in the rotating cylindrical vessel is approximately 4.015 cm.
Topper's Solved these Questions
Similar Questions
The product of the numbers 5623 and 6 in the scale of eight is
View SolutionA cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
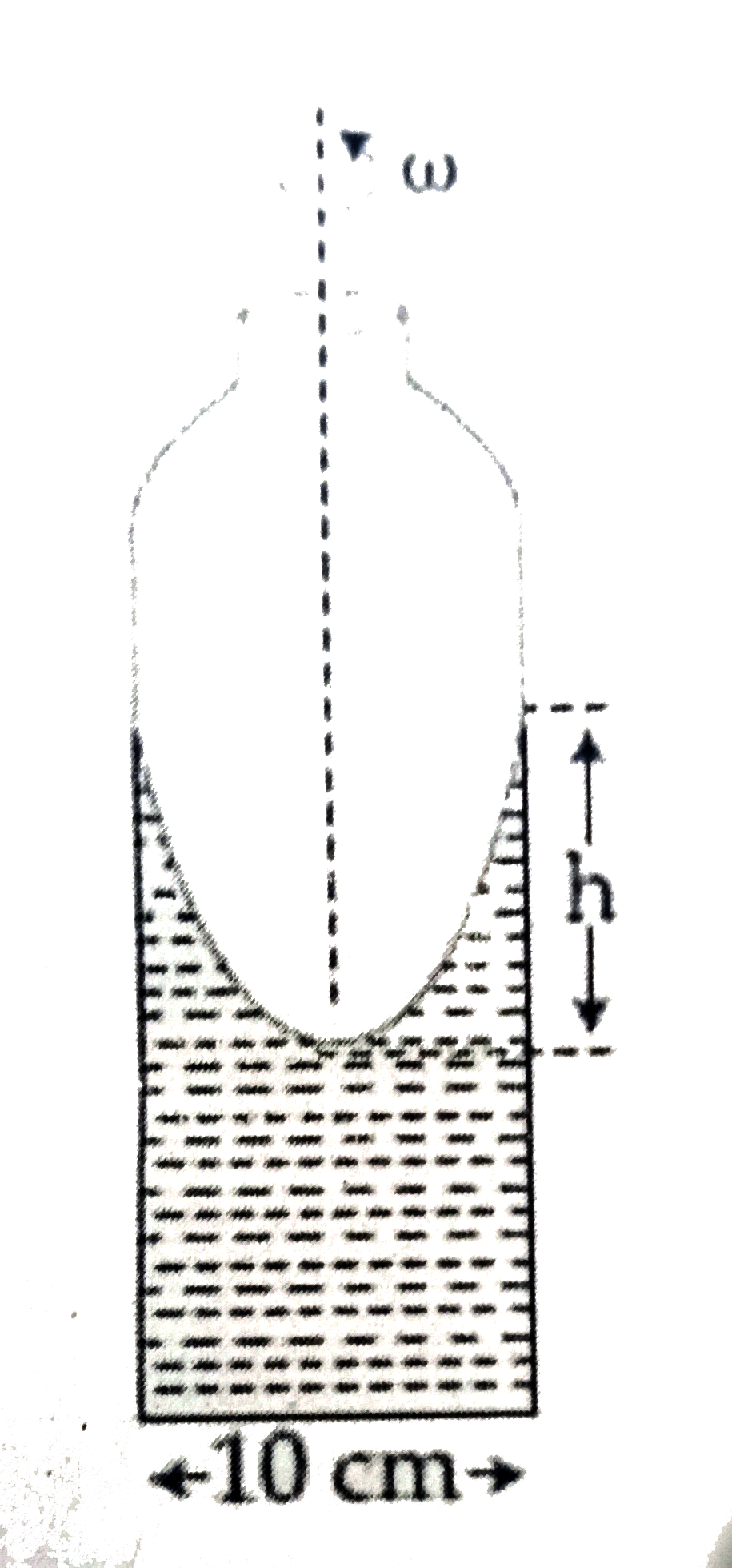 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
A8cmB2cmC40cmD4cm - Question 2 - Select One
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
Ah=2π2n2r2gBh=4π2n2r2gCh=π2r2n2gDh=π2r2n2g - Question 3 - Select One
A liquid is kept in a cylindrical jar, which is rotated about the cylindrical axis. The liquid rises at its sides. The radius of the jar is r and speed of rotation is Ω the difference in height at the centre and the sides of the jar is
Ar2ω2gBr2ω22gCgr2ω2D2gr2ω2
A liquid kept in a cylindrical vessel of radius 0.3 m is rotated with a speed 2 r.p.s. The difference in the height of the liquid at the centre of the vessel and at it's sides it
View SolutionA liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
View SolutionA liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
View SolutionA long cylinderical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis. The liquid rises up near the wall. If the radius of vessel is 5cm and its rotational speed is 2 rotatins per second, then the difference in the heights between the centre and the sides, in cm. will be :
View SolutionA long cylinderical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis. The liquid rises up near the wall. If the radius of vessel is 5cm and its rotational speed is 2 rotatins per second, then the difference in the heights between the centre and the sides, in cm. will be :
View Solution

